Критерий коши существования предела последовательности, предела функции

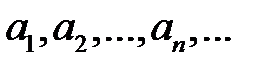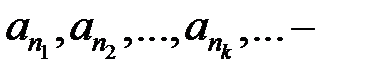Определение. Пусть задана последовательность и пусть - возрастающая последовательность натуральных чисел. Тогда последовательность подпоследовательность исходной последовательности.

Теорема.Последовательность 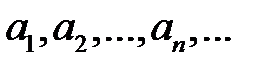имеет предел A тогда и только тогда, когда любая её подпоследовательность имеет предел, равный A.

Теорема. (Лемма Больцано-Вейерштрасса) Из любой ограниченной бесконечной последовательности можно извлечь подпоследовательность, сходящуюся к конечному пределу.

Определение.Последовательность 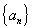называется фундаментальной, если для любого положительного 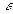существует такое 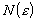, что для всех 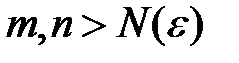разность значений 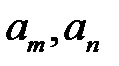по модулю меньше 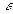, т.е. .

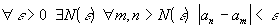Теорема .(Критерий Коши для последовательности) Предел последовательности существует тогда и только тогда, когда эта последовательность является фундаментальной.

Теорема .(Критерий Коши для функции) Условие: для любого 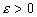существует такое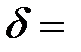 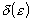, что для любых 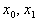из 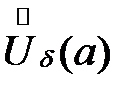разность значений функции 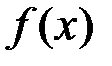в этих точках по абсолютной величине меньше 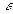, равносильно тому, что существует предел этой функции при 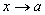, т.е. 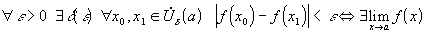. (1)

Определение .( предела функци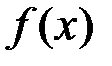и при 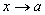по Гейне ). Говорят, что функция 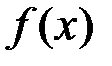имеет при 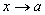предел 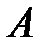, если для любой последовательности 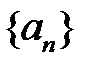такой, что 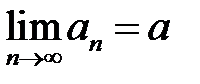и такой, что для всех 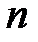выполнено неравенство 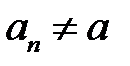, предел .

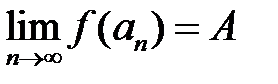Теорема.Определение предела по Коши, равносильно определению предела по Гейне.

НЕПРЕРЫВНОСТЬ. ТОЧКИ РАЗРЫВА.СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ

ОпределениеФункция 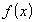называется непрерывнойв точке 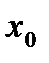, если 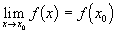, т.е. .

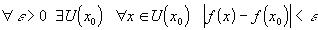Для непрерывности в точке 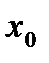используется обозначение .

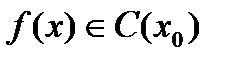Теорема. .Если функци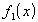и и 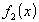непрерывны в точке 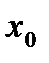, то сумма, разность, произведение и, если 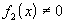, то и частное этих функций - тоже непрерывны в точке .

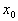Теорема (непрерывность сложной функции). Пусть 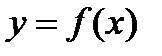непрерывна в точке 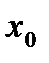, причем 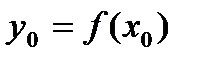. Пусть 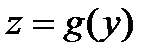непрерывна в точке 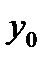. Тогда сложная функция 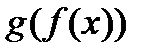непрерывна в точке .

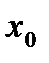Несколько сложнее теорема о пределе сложной функции.

Теорема .Пусть 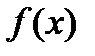определена в проколотой окрестности точки a, 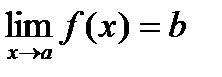. Пусть 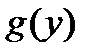определена в проколотой окрестности точки b и .

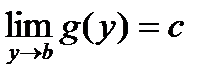Пусть, кроме того, выполняется хотя бы одно из двух условий:

1. 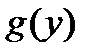непрерывна в точке ;

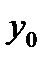2. Существует такая 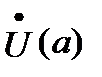, что .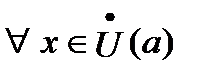

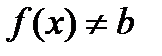Тогда существует 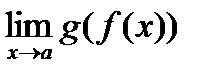и этот предел равен с.

Примечание. Обычно при вычислении пределов мы используем монотонные замены переменной и условие 2 выполняется.

Примечание . Если не выполняется ни одно из условий, то может оказаться, что предел 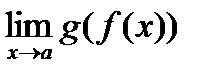не существует, либо существует, но не равен с.

Определение.Если функция не является непрерывной в точке 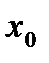, то говорят, что она разрывна в этой точке.

При этом предполагаем, что 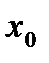является точкой из области определения функции.

Точки разрыва делятся на следующие классы.

Определение. Точкой устранимого разрыва называется такая точка 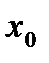, что существует 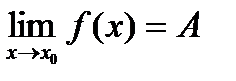, но 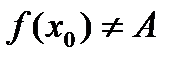. Таким образом, можно переопределить функцию так, чтобы получилась непрерывная функция.

Иногда к точкам устранимого разрыва относят такие точки 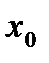, что существует 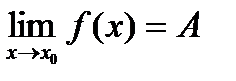, но при этом значение 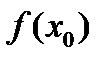не определено. В этом случае можно доопределить функцию в точке 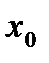так, чтобы получилась непрерывная функция.

Поясним сказанное примерами:

1. Пусть 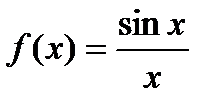. Эта функция не определена в точке 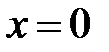, но её предел при 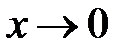существует и равен 1. Поэтому можно

доопределить функцию 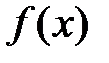, рассмотрев функцию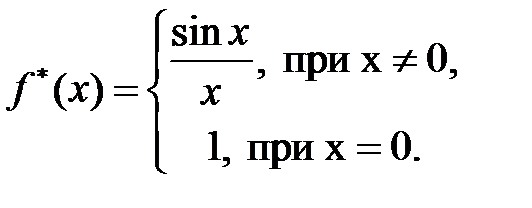

По определению, функция 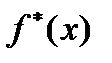– непрерывна в .

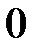1. Пусть

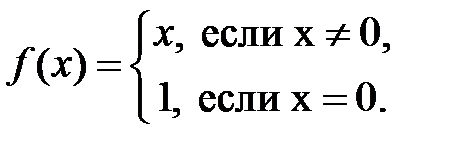
Переопределим функцию в точке 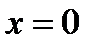, положив .

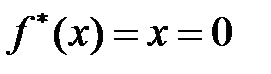Получилась непрерывная функция .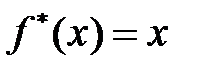

И в том, и в другом примере разрыв удалось устранить.

Определение 13.4.Точкой разрыва первого роданазывается точка ,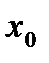

в которой существуют 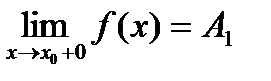и 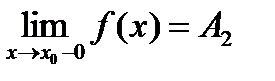, причем 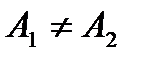и существует значение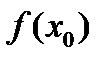

Например, функция 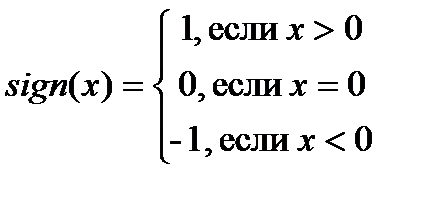обладает разрывом в точке 0 первого рода.

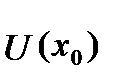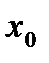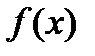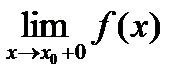Замечание. Монотонная в окрестности точки функция имеет и 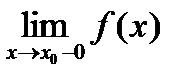. Поэтому она либо непрерывна в точке a, когда оба эти предела равны друг другу, либо имеет в ней разрыв первого рода, когда эти пределы различные.

Определение.Если хотя бы один из пределов 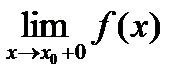, 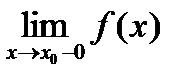не существует, или бесконечен, то говорят, что 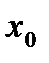– точка разрыва второго рода.