Распределенность терминов в суждениях

Напомню, что термины суждения - это субъект и предикат.

Если в суждении квантор все- то субъект распределен (обозначаем знаком +); если кванторнекоторые - то субъект не распределен (обозначаем знаком -).
Не забывайте, что суждения с квантором этотрассматриваются как общие.

Как правило, в утвердительных суждениях предикат не распределен; в отрицательных – распределен.

Получается так:

A I E O
S + - + -
P - - + +

Правила силлогизма

Правила терминов:

1. Средний термин должен быть распределен хотя бы в одной из посылок.
2. Термин, не распределенный в посылке, не может быть распределен и в заключении.

18.Диаграмма, служащая для мнемонического запоминания логических отношений между видами суждений по объединенной классификации. 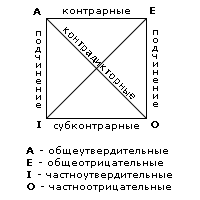Вершины квадрата обозначают вид суждения по объединенной классификации А , Е , 0 , I. Стороны и диагонали символизируют логические отношения между простыми суждениями (кроме эквивалентных). Верхняя сторона есть О отношение А и Е - противоположность (контрарность); нижняя сторона - отношение между I и O - частичная совместимость(субконтрарность);две вертикальные стороны - отношения между Аи I (левая), Е и О (правая) - подчинение; диагонали - отношения между А и О, Е иI- противоречие(контрадикторность).

Отношения противоположности– суждения находящиеся в отношении противоположности не могут быть одновременно истинными, но могут быть одновременно ложными.

Все мужчины галантны. Ни один мужчина не галантен. Если одно из противоположных истинно, то другое ложно, но не наоборот. А истинно, Е ложно. ∀ (x)(S(x) ⊃ P(x)) ⊃ ∀- (x)(S(x) ⊃ P-(x)) Если верно, что все S суть P, то неверно, что ни одно S не суть P.

Отношения противоречия– суждения находящиеся в состоянии противоречия не могут быть одновременно не ложными, не истинными. Если одно из них истинно, то другое непременно ложно, и наоборот. А истинно, O – ложно. ∀ (x)(S(x) ⊃ P(x)) ⊃ ∃- (x)(S(x) ⋀ P-(x)) Если верно, что все S суть P, то неверно, что некоторые S не суть P.

Отношения подчинения – суть отношений подчинения заключается в том, что истинность подчинённых суждений, гарантируется истинностью общих суждений. Ложность подчинённых, обуславливает ложность общих. A истинно, E – ложно. ∀ (x)(S(x) ⊃ P(x)) ⊃ ∃ (x)(S(x) ⋀ P(x)) Если верно, что все S суть P, то верно, что и некоторые S суть P. Отношения подпротивности – суждения находящиеся в отношении подпротивности не могут быть одновременно ложными, но могут быть одновременно истинными. Если одно из суждений ложно, то другое непременно истинно, но не наоборот.

§ 19. Разделительные -- это суждение вида "А есть B или C или D". Например, "Индейцы бывают или хорошие или живые". Суть разделительного силлогизма в том, что мы можем выбрать только одну из альтернатив.

1) S есть или А, или В, или С

2) или А, или В, или С есть Р когда в суждении остается место неопределенности

§ Условно-разделительные суждения -- это суждение вида "А есть B или C или D". Например, "Индейцы бывают или хорошие или живые". Суть разделительного силлогизма в том, что мы можем выбрать только одну из альтернатив.

Если А есть В, то С есть D или Е есть F

если есть А, то есть а, или b, или с Прим: « Если кто желает получить высшее образование, то он должен учиться или в университете, или в институте, или в академии»

Условные -- это силлогизм, одной из посылок которого является условное суждение. Условные силлогизмы делятся на два типа. — суждения, в которых сказуемое ограничивает отношение каким-либо условием (Если А есть В, то С есть D). Пример: «Если дождь пойдет, то почва будет мокрая». Для условных суждений

§ Основание — это (предыдущее) суждение, которое содержит условие.

§ Следствие — это (последующее) суждение, которое содержит следствие.

20.Сложные суждения состоят из ряда простых («Человек не стремится к тому, во что не верит, и любой энтузиазм, не подкрепляясь реальными достижениями, постепенно угасает»), каждое из которых в математической логике обозначается латинскими буквами (A, B, C, D… a, b, c, d…). В зависимости от способа образования различаютконъюнктивные, дизъюнктивные, импликационные, эквивалентные и отрицательные суждения.

Дизъюнктивные суждения образуются с помощью разделительных (дизъюнктивных) логических связок (аналогичных союзу «или»). Подобно простым разделительным суждениям, они бывают:

§ нестрогими (нестрогая дизъюнкция), члены которой допускают совместное сосуществование («то ли…, то ли…»). Записывается как ;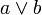

§ строгими (строгая дизъюнкция), члены которой исключают друг друга (либо одно, либо другое). Записывается как .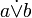

Импликационные суждения образуются с помощью импликации, (эквивалентно союзу «если …, то»). Записывается как 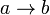или ab. В естественном языке союз «если …, то» иногда является синонимом союза «а» («Погода изменилась и, если вчера было пасмурно, то сегодня не одной тучи») и, в таком случае, означает конъюнкцию.

Конъюнктивные суждения образуются с помощью логических связок сочетания или конъюнкции (эквивалентно запятой или союзам «и», «а», «но», «да», «хотя», «который», «зато» и другим). Записывается как .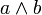

Эквивалентные суждения указывают на тождественность частей суждения друг другу (проводят между ними знак равенства). Помимо определений, поясняющих какой-либо термин, могут быть представлены суждениями, соединенными союзами «если только», «необходимо», «достаточно» (например: «Чтобы число делилось на 3, достаточно, чтобы сумма цифр, его составляющих, делилась на 3»). Записывается как 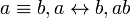(у разных математиков по-разному, хотя математический знак тождества всё-таки ).

Отрицательные суждения строятся с помощью связок отрицания «не». Записываются либо как a ~ b, либо как a b (при внутреннем отрицании типа «машина не роскошь»), а также с помощью черты над всем суждением при внешнем отрицании (опровержении): «не верно, что …» (a b).

21.Модальность - это явно или неявновыраженная в суждении дополнительная информация о логическом или фактическом статусе суждения, о регулятивных, оценочных, временных и других его характеристиках.
Наиболее важными и распространенными выступают такие виды модальности, как алетическая, деонтическая, эпистемическая и аксиологическая.
Алетическая модальность выражает характер связи между мыслимыми предметами, а следовательно, между субъектом и предикатом суждения. Модальными словами в русском языке, в этом случае, являются «возможно», «случайно» и их синонимы.
С точки зрения алетической модальности различают следующие разновидности суждений:
- ассерторические суждения или суждения о реальном факте. Например: «В России действительно осуществляется реформирование Вооруженных Сил». В таких суждениях модальность не выражена, констатируется лишь сам факт чего-либо;
- проблематические суждения или суждения о возможности чего-либо. Например: «В России может быть осуществлено реформирование Вооруженных Сил»;
- аподиктические суждения или суждения о необходимости чего-либо. Например: «В России необходимо осуществить реформирование Вооруженных Сил».
Деонтическая модальность распространяется только на деятельность людей, нравственные и правовые нормы их поведения в обществе. Она выражается с помощью таких слов, как «разрешается», «запрещается», «обязательно» и т. п.
В зависимости от характера норм деонтическая модальность имеет следующие разновидности:
- суждения о наличии (или отсутствии) какого-либо права. Они формируются с помощью слов «разрешено», «запрещено», «вправе» и других. Например: «Каждый имеет право на свободу и личную неприкосновенность» (правопредоставляющая норма) и «Запрещаются любые формы ограничения прав граждан при вступлении в брак и в семейные отношения по признакам социальной, расовой, национальной, языковой или религиозной принадлежности» (правозапрещающая норма);
- суждения о наличии (или отсутствии) какой либо обязанности. Они формулируются посредством слов «обязан», «должен», «необходимо» и др. Например: «Признание, соблюдение и защита прав и свобод человека и гражданина — обязанность государства».
Эпистемическая модальность характеризует степень достоверности знания. Она выражается с помощью слов «доказано», «недоказуемо», «опровергнуто» и им подобных. Выделяют две разновидности эпистемической модальности:
- суждения, основанные на вере. Например: «Верю в наступление лучшей жизни»;
- суждения, основанные на знании. Например: «По показаниям свидетелей Николаев не участвовал в похищении материальных ценностей».
Аксиологическая модальность выражает отношение человека к материальным и духовным ценностям. Она включает такие слова, как «хорошо», «плохо» и т. п. Например: «Безразличное отношение к государственному имуществу приводит к его утрате» или «Хорошо, что я не опоздал на занятия в институт».

Законы логики

§ Закон тождества - любая мысль (любое рассуждение) обязательно должна быть равна (тождественна) самой себе, т. е. она должна быть ясной, точной, простой, определенной. Говоря иначе, этот закон запрещает путать и подменять понятия в рассуждении (т. е. употреблять одно и то же слово в разных значениях или вкладывать одно и то же значение в разные слова), создавать двусмысленность, уклоняться от темы и т п. Например, непонятен смысл фразы: «Из-за рассеянности на турнирах шахматист неоднократно терял очки». Очевидно, что по причине нарушения закона тождества появляются неясные высказывания (суждения). Символическая запись этого закона выглядит так: а →а (читается: «Если а, то а»), где а — это любое понятие, высказывание или целое рассуждение.

§ Закон исключённого третьего - уждения бывают противоположными и противоречащими. Например, суждения: «Сократ высокий», «Сократ низкий», — являются противоположными, а суждения: «Сократ высокий», «Сократ невысокий», — противоречащими. В чем разница между противоположными и противоречащими суждениями? Нетрудно заметить, что противоположные суждения всегда предполагают некий третий, средний, промежуточный вариант. Для суждений: «Сократ высокий», «Сократ низкий», — третьим вариантом будет суждение: «Сократ среднего роста». Противоречащие суждения, в отличие от противоположных, не допускают или автоматически исключают такой промежуточный вариант. Как бы мы ни пытались, мы не сможем найти никакого третьего варианта для суждений: «Сократ высокий», «Сократ невысокий» (ведь и низкий, и среднего роста — это все невысокий).
Именно в силу наличия третьего варианта противоположные суждения могут быть одновременно ложными.

§ Закон противоречия - одно суждение что-то утверждает, а другое то же самое отрицает об одном и том же объекте, в одно и то же время и в одном и том же отношении, то они не могут быть одновременно истинными. Например, два суждения: «Сократ высокий», «Сократ низкий» (одно из них нечто утверждает, а другое то же самое отрицает, ведь высокий — это не низкий, и наоборот), — не могут быть одновременно истинными, если речь идет об одном и том же Сократе, в одно и то же время его жизни и в одном и том же отношении, т. е. если Сократ по росту сравнивается не с разными людьми одновременно, а с одним человеком. Понятно, что когда речь идет о двух разных Сократах или об одном Сократе, но в разное время его жизни, например в 10 лет и в 20 лет, или один и тот же Сократ и в одно и то же время его жизни рассматривается в разных отношениях, например он сравнивается одновременно с высоким Платоном и низким Аристотелем, тогда два противоположных суждения вполне могут быть одновременно истинными, и закон противоречия при этом не нарушается. Символически он выражается следующей тождественно-истинной формулой: (а Λ а), (читается: «Неверно, что а и не а»), где а — это какое-либо высказывание.
Говоря иначе, логический закон противоречия запрещает что-либо утверждать и то же самое отрицать одновременно.

§ Закон достаточного основания - Закон достаточного основания утверждает, что любая мысль (тезис) для того, чтобы иметь силу, обязательно должна быть доказана (обоснована) какими-либо аргументами (основаниями), причем эти аргументы должны быть достаточными для доказательства исходной мысли, т. е. она должна вытекать из них с необходимостью (тезис должен с необходимостью следовать из оснований).
Приведем несколько примеров. В рассуждении: «Это вещество является электропроводным (тезис), потому что оно — металл (основание)», — закон достаточного основания не нарушен, так как в данном случае из основания следует тезис (из того, что вещество металл, вытекает, что оно электропроводно). А в рассуждении: «Сегодня взлетная полоса покрыта льдом (тезис), ведь самолеты сегодня не могут взлететь (основание)», — рассматриваемый закон нарушен, тезис не вытекает из основания (из того, что самолеты не могут взлететь, не вытекает, что взлетная полоса покрыта льдом, ведь самолеты могут не взлететь и по другой причине). Так же нарушается закон достаточного основания в ситуации, когда студент говорит преподавателю на экзамене: «Не ставьте мне двойку, спросите еще (тезис), я же прочитал весь учебник, может быть, и отвечу что-нибудь (основание)». В этом случае тезис не вытекает из основания (студент мог прочитать весь учебник, но из этого не следует, что он сможет что-то ответить, так как он мог забыть все прочитанное или ничего в нем не понять и т. п.).

§ Законы де Моргана

§ Законы дедуктивных умозаключений

§ Закон Клавия

§ Законы деления