Методические указания к выполнению контрольной работы. Основы метрологии и стандартизации

Основы метрологии и стандартизации

Методические указания к контрольным работам

Для студентов заочной формы обучения

Введение
1 Общие методические указания
2 Рабочая программа
3 Методические указания к выполнению контрольной работы
4 Контрольное задание
Рекомендуемая литература
Приложение А
Приложение Б
Приложение В
Приложение Г

Введение

С увеличением объема измерений возрастает роль метрологии – науки об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности. Чем точнее выполнены измерения, тем более точны знания о состоянии объекта и его свойствах, тем меньше экономические потери из-за меньшей вероятности выхода его из строя.

Метрологию органично дополняет стандартизация– деятельность, направленная на достижение оптимальной степени упорядочения в определенной области.

Основные цели метрологии: повышение качества выпускаемой продукции, эффективности управления производством, уровня автоматизации производственных процессов; обеспечение взаимозаменяемости деталей, узлов и агрегатов, создание условий для кооперирования производства и развития специализации производства; повышение эффективности научно-исследовательских, проектно-конструкторских работ, экспериментов и испытаний; обеспечение достоверного учёта и повышение эффективности использования материальных ценностей и энергетических ресурсов; повышение эффективности мероприятий по контролю условий труда, охране окружающей среды, рациональному использованию природных ресурсов.

Основными задачами метрологии являются: разработка общей теории измерений; установление единиц физических величин и их систем; создание методов и средств измерений; установление единиц физических величин и их систем; создание методов и средств измерений, методов определения точности измерений; обеспечение единства измерений и единообразия средств измерений; создание эталонов и образцовых средств измерений; разработка методов передачи размеров единиц от эталонов или образцовых средств измерений рабочим средствам измерений.

Учебным планом запланировано 8 часов лекций, 8 часов практических занятий, выполнение одной контрольной работы и сдача зачета.

Общие методические указания

Необходимо изучить теоретический материал, выполнить одну контрольную работу, выполнить задания на практических занятиях, сдать зачет.

Теоретические вопросы следует изучать, руководствуясь рабочей программой, приведенной в разделе 2 настоящих методических указаний. В конце каждой темы даны вопросы для самопроверки усвоения материала.

При выполнении практических занятий необходимо пользоваться соответствующими методическими указаниями (п. 3).

При сдаче зачета преподавателю должна быть предъявлена контрольная работа, допущенная к собеседованию.

Рабочая программа

Общие вопросы метрологии

2.1.1 Введение. Задачи метрологии. Единицы измерений.Развитие метрологии и стандартизации в Республике Беларусь и за рубежом. Республиканские и международные метрологические организации. Главные функции измерений. Место дисциплины в учебном процессе специальности. Содержание и задачи метрологии. Основные понятия и термины. Основные и производные единицы СИ. Размерность физических величин. Кратные и дольные единицы. Эталоны единиц физических величин ([1], Стр. 5 – 6, 30; [2], Стр.5-10, 30–36; [3], Стр.10; [4], Стр.18 – 22, 112– 122).

2.1.2 Виды и методы измерений.

Прямые, косвенные, совокупные и совместные измерения. Метод непосредственной оценки и метод сравнения (нулевой, дифференциальный, замещения, совпадения). Примеры ([1], Стр.6–8; [2], Стр.17-20; [3], Стр.20–21).

2.1.3 Средства измерений.

Классификация средств измерений: по принципу действия, по способу образования показаний, по способу получения числового значения измеряемой величины, по точности, по условиям применения, по степени защищенности от внешних магнитных и электрических полей, по прочности и устойчивости против механических воздействий и перегрузок, по стабильности, по чувствительности, по пределам и диапазонам измерений. Метрологические и неметролоческие характеристики средств измерений ([2], Стр.20-23; [3], Стр. 23–38).

2.1.4 Измерительная информация и методы ее преобразования.

Основные виды сигналов, используемых в средствах измерений: непрерывные по информативному параметру и времени сигналы; непрерывные по информативному параметру и дискретные по времени сигналы; сигналы, непрерывные по времени и квантованные по информативному параметру; сигналы, дискретные по времени и квантованные по информативному параметру. Модели квазидетерминированных, случайных сигналов и сигналов в виде комбинации случайной и детерминированной составляющих ([4], Стр.59—63).

2.1.5 Обобщенные структурные схемы электроизмерительных приборов.

Аддитивная и мультипликативная составляющие погрешности. Формирование сигнала в средствах измерений прямого и уравновешивающего преобразования (с полной и неполной компенсацией сигнала) ([1], Стр. 24; [3], Стр. 29–30).

2.1.6 Погрешности обработки результатов измерений.

Истинное и действительное значение величины. Виды погрешностей: инструментальная, методическая, абсолютная, относительная, приведенная. Статическая и динамическая погрешности (основная и дополнительная). Погрешность приближения, погрешность от изменения внутренних параметров измерительных устройств, погрешность от действия внутренних дестабилизирующих факторов ([1], Стр.22–29; [2], Стр.31-40; [3], Стр.35–43).

2.1.7 Систематическая погрешность.

Постоянные систематические погрешности. Закономерно изменяющиеся систематические погрешности: прогрессирующие, периодические и изменяющиеся по сложному непериодическому закону. Обнаружение и исключение систематических погрешностей. Устранение постоянных систематических погрешностей (метод замещения, метод противопоставления, метод компенсации погрешности по знаку). Устранение прогрессирующих систематических погрешностей ([1], Стр. 9–21; [3], Стр.67–71).

2.1.8 Случайная погрешность.

Случайная погрешность и законы ее распределения (нормальный, равномерный, трапециевидный, треугольный, в виде d-функции) ([1], Стр. 11–22; [3], Стр. 44–59).

2.1.9 Точечная и интервальная характеристики погрешностей.

Точность и правильность измерений, поправка, математическое ожидание, дисперсия, доверительный интервал, доверительная вероятность ([3], Стр.63–67; [4], Стр.78–84).

2.1.10 Оценка погрешности результатов прямых и косвенных измерений

2.1.10.1. Равноточные результаты наблюдений. Оценка погрешности результатов прямых измерений. Форма записи результатов измерений. Правила округления.

2.1.10.2 Оценка погрешности косвенных измерений при отсутствии и наличии корреляции результатов прямых измерений. Примеры. Суммирование сильно- и слабокоррелированных погрешностей ([3], Стр. 72–84, 85–88).

2.1.11 Классы точности средств измерений.

Класс точности средств измерений. Пределы допускаемых основных абсолютной, приведенной и относительной погрешностей. Пределы допускаемой дополнительной погрешности. Примеры обозначения классов точности средств измерения ([3], Стр.39–43; [4], Стр. 148–153).

2.1.12 Аппроксимация функций распределения случайных погрешностей Аналитический, графический и табличный методы аппроксимации.

2.1.13 Поверка и испытание средств измерения.

2.1.13.1 Виды поверок. Средства измерений, подлежащие поверке. Порядок проведения поверки. Испытания средств измерения.

2.1.13.2 Методы поверки. Выбор образцового средства измерения. Операции, выполняемые при поверке.

2.2 Вопросы для самопроверки

1 Назовите основные отечественные и зарубежные метрологические организации.

2 Назовите главные функции измерений.

3 Назовите задачи метрологии.

4 Какие основные и производные единицы СИ Вы знаете?

5 Как определяют размерность физических величин?

6 Как образуются кратные и дольные единицы?

7 Какие эталоны единиц физических величин Вы знаете?

8 Назовите основные виды и методы измерений.

9 В чем сущность основных методов измерений?

10 Как классифицируют средства измерений?

11 Назовите основные метрологические и неметролоческие характеристики средств измерений.

12 Какие основные виды сигналов используют в средствах измерений?

13 Какие составляющие погрешности называют аддитивными и мультипликативными?

14 Как формируется сигнал в средствах измерений прямого и уравновешивающего преобразования?

15 Что такое истинное и действительное значение величины?

16 Дайте определение инструментальной, методической, абсолютной, относительной, приведенной, статической и динамической погрешности.

17 Что такое погрешность приближения, погрешность от изменения внутренних параметров измерительных устройств, погрешность от действия внутренних дестабилизирующих факторов?

18 Дайте определение систематической погрешности.

19 Какие бывают систематические погрешности?

20 Как устраняют систематические погрешности?

21 Дайте определение случайной погрешности.

22 Какие законы распределения случайной погрешности Вы знаете?

23 Что такое точность и правильность измерений?

24 Что такое поправка?

25 Что такое математическое ожидание?

26 Что такое дисперсия, доверительный интервал, доверительная вероятность?

27 Как оценивают погрешности результатов прямых и косвенных измерений?

28 Как оценивают погрешности результатов косвенных измерений?

29 Как следует записывать результаты измерений?

30 Как округляют результаты измерений?

31 Как следует суммировать сильно- и слабокоррелированные погрешности?

32 Дайте определение классу точности средств измерений.

33 Как определяют пределы допускаемых основных абсолютной, приведенной и относительной погрешностей?

34 Приведите примеры обозначения классов точности.

35 Опишите аналитический, графический и табличный методы аппроксимации функций распределения случайных погрешностей.

36 Какие бывают виды поверок средств измерений?

37 Какие средства измерений подлежат поверке?

38 Какой порядок проведения поверки средств измерения?

39 Как выбирают образцовое средство измерения при поверке?

40 Какие операции выполняют при поверке средств измерений?

41 Опишите подробно каждую операцию, выполняемую при поверке.

2.3 Основы стандартизации (2ч).

Государственная система стандартизации. Цели и задачи стандартизации и государственные стандарты. Разработка стандартов. Стадии разработки стандартов. Качество продукции и стандарты. Система международных стандартов ИСО 9000 ([6], Стр. 1–17).

2.4 Вопросы для самопроверки.

1 Что такое государственная система стандартизации?

2 Каковы цели и задачи стандартизации?

3 Назовите стадии разработки стандартов.

4 Какова цель системы международных стандартов ИСО 9000?

2.5 Национальная система сертификации Республики Беларусь.

Цель создания. Виды деятельности. Основные правила системы. Порядок проведения сертификации. Обязательная и добровольная сертификация. Аккредитация органов по сертификации и испытательных лабораторий [7].

2.6 Вопросы для самопроверки.

1 Что собой представляет система сертификации?

2 Какой порядок проведения сертификации?

3 В чем особенности обязательной и добровольной сертификации?

4 Какой порядок проведения аккредитации органов по сертификации и испытательных лабораторий?

Методические указания к выполнению контрольной работы

После изучения теоретического материала следует приступить к выполнению контрольной работы. Цель –умение применить полученные знания на

практике. Студент должен выполнить тот вариант, задачи, порядковый номер которого совпадает с последней цифрой номера его зачетной книжки. Контрольная работа должна выполняться аккуратно в соответствии с общими требованиями. В конце работы необходимо привести список использованной литературы. При наличии ошибок работа возвращается на доработку. Контрольная работа считается зачтенной только после прохождения студентом собеседования на кафедре, где она рецензировалась. Во время собеседования проверяется самостоятельность выполнения контрольной работы, глубина усвоения теоретического материала.

При статистической обработке группы результатов наблюдений следует выполнить следующие операции [1].

3.1 Исключить известные систематические погрешности из результатов наблюдений.

3.2 Вычислить среднее арифметическое исправленных результатов наблюдений, принимаемое за результат измерения :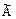

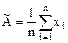. (3.1)

3.3 Вычислить оценку среднего квадратического отклонения (СКО) результата наблюдения

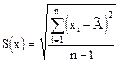, (3.2)

где x_i – i-й результат наблюдения;

n – число результатов наблюдений.

3.4 Среднее квадратическое отклонение 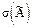результата измерения оценивают по формуле

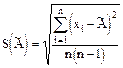. (3.3)

3.5 Проверить гипотезу о том, что результаты наблюдений принадлежат нормальному распределению (приложение А). Проверку этой гипотезы проводить с уровнем значимости q от 10 до 2 %. Конкретные значения уровней значимости должны быть указаны в методике выполнения измерений.

При n>50 для проверки принадлежности результатов наблюдений к нормальному распределению по ГОСТ 11.006–74 предпочтительным является один из критериев: c² Пирсона или w² Мизеса-Смирнова. Если 15<n<50, то предпочтительным является составной критерий (см. приложение А). При 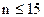принадлежность результатов наблюдений к нормальному распределению не проверяют. При этом нахождение доверительных границ случайной погрешности по методике, предусмотренной ГОСТ 8.207–76, возможно в том случае, если заранее известно, что результаты наблюдения принадлежат нормальному распределению.

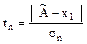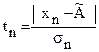3.6 Если результаты наблюдений удовлетворяют нормальному закону распределения, то грубые погрешности исключают в соответствии со стандартом. Так, при известном среднем квадратическом отклонении s_n критерием анормальности служит соотношение между или и значением b, которое для данного n и принятой вероятности (уровня значимости) 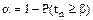берут из таблицы В.1. Если 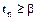, то результат х₁ (или х_n) анормальный. При неизвестном s_n критерием анормальности служит соотношение между 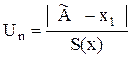или 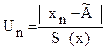и значением b, которое для данного n и принятой вероятности 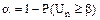берут из таблицы В.2. Если 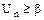, то результат х₁ (или х_n) отбрасывается как анормальный. В этом случае заново вычисляют результат измерения и оценку СКО результата измерения.

3.7 Доверительные границы e (без учета знака) случайной погрешности результата измерения находят по формуле

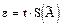, (3.4)

где t – коэффициент Стьюдента, который в зависимости от доверительной вероятности Р_и числа результатов наблюдений n находят по таблице Б.1.

Доверительную вероятность Р принимают равной 0,95, допускается указывать границы для доверительной вероятности Р=0,99. В особых случаях, например при измерениях, результаты которых имеют значение для здоровья людей, допускается вместо Р=0,99 принимать более высокую доверительную вероятность.

3.8 Вычислить границы неисключенной систематической погрешности (неисключенных остатков систематической погрешности) результата измерения (НСП).

Неисключенная систематическая погрешность результата измерения образуется из составляющих, в качестве которых могут быть неисключенные систематические погрешности: метода, средств измерения, вызванные другими источниками. Границами составляющих НСП принимают, например, пределы допускаемых основных и дополнительных погрешностей средств измерений, если случайные составляющие погрешности пренебрежимо малы.

При суммировании составляющих НСП результата измерения НСП средств измерения каждого типа и погрешности поправок рассматривают как случайные величины. Если данные о виде распределения случайных величин отсутствуют, то их распределения принимают за равномерные. При равномерном распределении НСП их границы (без учета знака) вычисляют по формуле

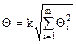, (3.5)

где Qi – граница i-й неисключенной систематической погрешности;

к– коэффициент, определяемый принятой доверительной вероятностью.

Коэффициент k принимают равным 1,1 при доверительной вероятности Р=0,95, а при доверительной вероятности Р=0,99 коэффициент k принимают равным 1,4, если число суммируемых неисключенных систематических погрешностей более четырех (m>4). Если же число суммируемых погрешностей равно четырем или менее четырех, то значение k определяют по графику [5].

Доверительную вероятность для вычисления границ неисключенной систематической погрешности принимают той же, что и при вычислении доверительных границ случайной погрешности результата измерения.

3.9 Вычисление доверительных границ погрешности результата измерения.

Если отношение 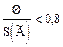, то неисключенными систематическими погрешностями по сравнению со случайными пренебрегают и принимают, что граница погрешности результата D=e. Если 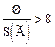, то случайной погрешностью по сравнению с систематическими пренебрегают и принимают, что границы погрешности результата D=Q. Погрешность, возникающая из-за пренебрежения одной из составляющих погрешности результата измерения при выполнении указанных неравенств, не превышает 15 %.

Если представленные выше неравенства не выполняются, то допускается границы погрешности результата измерения D (без учета знака) вычислять по формуле

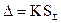, (3.6)

где K – коэффициент, зависящий от соотношения случайной и неисключенной систематической погрешностей;

S_S – оценка суммарного среднего квадратического отклонения результата измерения.

При этом S_S вычисляют по формуле 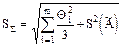, а коэффициент

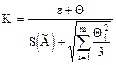. (3.7)

3.10 Форма записи результатов измерений.

Оформление результатов измерений производят по ГОСТ 8.011-72.

3.10.1 При симметричной доверительной погрешности результаты измерений представляют в форме:

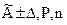, (3.8)

где 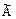– результат измерения.

Числовое значение результата измерения должно оканчиваться цифрой того же разряда, что и погрешности D.

3.10.2 При отсутствии данных о виде функций распределений составляющих погрешности результата и необходимости дальнейшей обработки результатов или анализа погрешностей результаты измерений представляют в форме .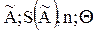

Правила округления

1 Погрешность результата измерения указывается двумя значащими цифрами (все цифры, стоящие справа после нулей), если первая из них равна 1 или 2, и одной, если первая есть 3 и более. Округление производится лишь в окончательном ответе, а все предварительные расчеты выполняются не менее чем с одним-двумя лишними знаками.

Контрольное задание

4.1 Задача контрольной работы

4.1.1 Произвести оценку результата измерения постоянного тока по результатам 17 наблюдений с помощью амперметра, имеющего предел основной приведенной погрешности g. Шкала применяемого прибора равномерная. Нулевая отметка находится на краю шкалы. Конечное значение диапазона измерения C_N . Известные систематические погрешности исключены. Неисключенные систематические погрешности измерительного прибора определяются пределом допускаемой абсолютной погрешности. Задачу решить для заранее выбранного уровня значимости q₁/2=5 %, q₂=5 %. Статистическую обработку результатов наблюдений выполнить для доверительной вероятности Р. Исходные данные приведены в таблице 1.

Таблица 1 – Исходные данные

№ варианта	Результаты наблюдений I	Р	g	xN
	5,4	5,9	5,8	5,9	5,6	5,1	4,8	4,9	5,1	5,3	5,4	5,6	5,0	5,3	5,1	5,6	5,6	0,99	1,5
	5,4	4,8	4,9	3,3	4,8	5,4	4,2	5,2	5,8	4,7	5,4	4,7	4,8	5,2	5,1	4,4	5,2	0,95
	31,5	30,7	29,9	31,8		31,7	30,9	29,5	31,9	30,6	29,5	31,9	30,5	29,6	31,5	30,4	31,3	0,95
	7,9	7,1	7,3	7,5	7,6	7,2	7,4	7,1	6,8	6,9		7,2	7,2	7,1		6,9	7,4	0,99
	32,2	28,5	29,8	31,4	30,9		30,2	32,2	32,3	33,3	30,7	33,2	26,6	29,4	31,2	28,2	32,1	0,95
	5,2	5,7	5,5	5,2	6,7	7,8	7,0	5,6	6,0	5,1	6,7	6,1	6,9	7,3	6,2	7,8	6,2	0,99	1,5
	10,3	7,4	8,4	9,6	9,3	8,5	8,7	9,6	10,3		9,1	11,1		8,1	8,6	7,2	10,2	0,95
	0,63	1,35	0,83	1,8	1,60	1,1	1,79	0,55	0,89	1,59	1,22	1,76	1,69	1,61	1,24	0,75	1,67	0,95	2,5
	7,5	6,4	7,3	7,1	6,8	6,8	7,5	7,5	7,7	7,0	7,8	5,7	6,6	7,2	6,3	7,5	7,2	0,99
	44,3	44,4	44,2	44,1		45,2	44,7	44,9	44,1	44,2	44,4	44,7	45,1	44,9	44,2	44,3	44,6	0,95
	5,11	5,29	4,53	5,3	4,54	4,81	4,31	5,01	5,09	6,03	5,89		4,59	4,63	4,71	4,89	5,95	0,99
	71,4	72,5	73,2	69,3	73,5	74,7		72,4	72,1	70,6	70,5	72,9	70,6	71,4	70,7	72,6	69,4	0,95
		4,9		4,9	4,9			5,1		4,9				4,9	4,9	4,9		0,99
		50,4	50,3	50,2	51,6	50,8	51,4	51,7	59,3	50,6	50,3	50,1	55,7		51,5	51,2	51,1	0,95
	6,78	6,94	7,1	6,17	6,64	6,32	6,97	6,9	6,95	6,41	6,05	7,05	6,85	7,0	6,91	6,25	6,77	0,99	1,5
		7,8	5,8	8,4	7,8	6,5	5,2	8,4	7,2	8,2	6,8	8,5	6,3	6,9	5,9	8,5	7,3	0,95
	31,5	30,7	29,9	31,8		31,7	30,9	29,5	31,9	30,6	29,5	31,9	30,5	29,6	31,5	30,4	31,3	0,95
	50,6	50,7		59,3	51,1	78,3		53,3	54,2	50,3	55,6	56,1		88,3	52,1	51,1	50,2	0,99
	73,62	73,38	74,58	74,33	74,9	73,83	72,7	74,5	73,18	74,63	72,62	72,82	73,76	74,51	73,45	74,23	73,37	0,95
	3,17	3,26	3,33	3,35	3,37	3,30	3,22	3,27	3,21	3,24	3,33	3,37	3,31	3,39	3,38	3,21	3,17	0,95
	5,5	5,8	5,8	5,9	5,6	5,1	4,8	4,9	5,1	5,3	5,4	5,6	5,0	5,3	5,1	5,6	5,6	0,99	1,0
	5,3	4,8	4,9	3,3	4,8	5,4	4,2	5,2	5,8	4,7	5,4	4,7	4,8	5,2	5,1	4,4	5,2	0,95
	31,4	30,7	29,9	31,8		31,7	30,9	29,5	31,9	30,6	29,5	31,9	30,5	29,6	31,5	30,4	31,3	0,95	1,5
	7,8	7,1	7,3	7,5	7,6	7,2	7,4	7,1	6,8	6,9		7,2	7,2	7,1		6,9	7,4	0,99	1,5
	32,1	28,5	29,8	31,4	30,9		30,2	32,2	32,3	33,3	30,7	33,2	26,6	29,4	31,2	28,2	32,1	0,95	1,5
	5,1	5,7	5,5	5,2	6,7	7,8	7,0	5,6	6,0	5,1	6,7	6,1	6,9	7,3	6,2	7,8	6,2	0,99	1,5
	10,2	7,4	8,4	9,6	9,3	8,5	8,7	9,6	10,3		9,1	11,1		8,1	8,6	7,2	10,2	0,95
	0,62	1,35	0,83	1,8	1,60	1,1	1,79	0,55	0,89	1,59	1,22	1,76	1,69	1,61	1,24	0,75	1,67	0,95
	7,4	6,4	7,3	7,1	6,8	6,8	7,5	7,5	7,7	7,0	7,8	5,7	6,6	7,2	6,3	7,5	7,2	0,99
	44,3	44,4	44,2	44,1		45,2	44,7	44,9	44,1	44,2	44,4	44,7	45,1	44,9	44,2	44,3	44,6	0,95
	5,10	5,29	4,53	5,3	4,54	4,81	4,31	5,01	5,09	6,03	5,89		4,59	4,63	4,71	4,89	5,95	0,99	1,5
	71,3	72,5	73,2	69,3	73,5	74,7		72,4	72,1	70,6	70,5	72,9	70,6	71,4	70,7	72,6	69,4	0,95
	4,9	4,9		4,9	4,9			5,1		4,9				4,9	4,9	4,9		0,99
	50,1	50,4	50,3	50,2	51,6	50,8	51,4	51,7	59,3	50,6	50,3	50,1	55,7		51,5	51,2	51,1	0,95
	6,77	6,94	7,1	6,17	6,64	6,32	6,97	6,9	6,95	6,41	6,05	7,05	6,85	7,0	6,91	6,25	6,77	0,99	1,5
	7,9	7,8	5,8	8,4	7,8	6,5	5,2	8,4	7,2	8,2	6,8	8,5	6,3	6,9	5,9	8,5	7,3	0,95
	31,4	30,7	29,9	31,8		31,7	30,9	29,5	31,9	30,6	29,5	31,9	30,5	29,6	31,5	30,4	31,3	0,95
	50,5	50,7		59,3	51,1	78,3		53,3	54,2	50,3	55,6	56,1		88,3	52,1	51,1	50,2	0,99
	73,61	73,38	74,58	74,33	74,9	73,83	72,7	74,5	73,18	74,63	72,62	72,82	73,76	74,51	73,45	74,23	73,37	0,95
	3,15	3,26	3,33	3,35	3,37	3,30	3,22	3,27	3,21	3,24	3,33	3,37	3,31	3,39	3,38	3,21	3,17	0,95
	8,9	7,8	5,8	8,4	7,8	6,5	5,2	8,4	7,2	8,2	6,8	8,5	6,3	6,9	5,9	8,5	7,3	0,95
	31,4	30,7	29,9	31,8		31,7	30,9	29,5	31,9	30,6	29,5	31,9	30,5	29,6	31,5	30,4	31,3	0,95
	50,5	50,7		59,3	51,1	78,3		53,3	54,2	50,3	55,6	56,1		88,3	52,1	51,1	50,2	0,99
	73,61	73,38	74,58	74,33	74,9	73,83	72,7	74,5	73,18	74,63	72,62	72,82	73,76	74,51	73,45	74,23	73,37	0,95
	3,16	3,26	3,33	3,35	3,37	3,30	3,22	3,27	3,21	3,24	3,33	3,37	3,31	3,39	3,38	3,21	3,17	0,95

Рекомендуемая литература

1 Измерение электрических и неэлектрических величин: Учеб. пособие для вузов /Н.Н. Евтихиев, Я.А. Купершмидт, В.Ф. Папуловский, В.Н. Скугоров; Под общ. ред. Н.Н. Евтихиева.– М.: Энергоатомиздат, 1990. – 352с. : ил.

2 Бурдун Г.Д. Основы метрологии: Учеб. пособие для вузов. - 3-е изд. перераб. и доп./ Г.Д. Бурдун, Б.Н.Марков.–М. : Изд-во стандартов, 1985.-256 с. : ил.

3 Атамалян Э. Г. Приборы и методы измерения электрических величин: Учеб. пособие для студ. вузов. - 2-е изд., перераб. и доп. – М. : Высш. шк., 1989. - 384 с. : ил.

4 Шишкин И.Ф. Теоретическая метрология: Учебник для вузов.– М. : Из-во стандартов, 1991. – 492с. : ил.

5 ГОСТ 8.207 - 76. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений. - М. : Изд-во стандартов, 1978. - 12 с. : ил

6 СТБ 1.0-93. Государственная система стандартизации Республики Беларусь. – Мн. : Издание официальное, 1993.-19 с.

7 Гамидуллаев С.Н. Сертификация продукции и услуг: Учеб. пособие /С.Н.Гамидуллаев, И.В.Павлов, А.И.Потапов.–СПб. : РИО СПб филиала РТА. 2001.–168 с. : ил.

Приложение А

(рекомендуемое)

Проверка нормального закона распределения результатов наблюдений

При числе результатов наблюдений n < 50 нормальность их распределения проверяют при помощи составного критерия.

Критерий 1. Вычисляют отношение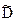

,

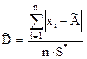где S^* -суммарная оценка среднего квадратического отклонения, вычисляемая по формуле

.

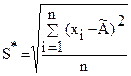Результаты наблюдений можно считать распределенными нормально, если

,

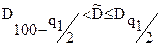где 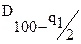и 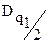- квантили распределения, получаемые из таблицы А.1 по данным n, q₁/2 и 100- q₁/2, причем q₁ - заранее выбранный уровень значимости критерия.

Таблица А.1 - Статистика D

n	q1/2×%	(100 - q1/2)×%
	1 %	5 %	95 %	99 %
	0,9137	0,8884	0,7236	0,6829
	0,9001	0,8768	0,7304	0,6950
	0,8901	0,8686	0,7360	0,7040
	0,8826	0,8625	0,7404	0,7110
	0,8769	0,8578	0,7440	0,7167
	0,8682	0,8508	0,7496	0,7256
	0,8648	0,8481	0,7518	0,7291

Критерий 2. Можно считать, что результаты наблюдений принадлежат нормальному распределению, если не более m разностей 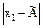превзошли значение

Z_p/2×S.

где S - оценка среднего квадратического отклонения, вычисляемая по формуле

,

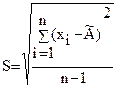где Z_p/2 - верхняя квантиль распределения нормированной функции Лапласа, отвечающая вероятности P/2.

Значения P определяются из таблицы А.2 по выбранному уровню значимости q₂ и числу результатов наблюдений n.

При уровне значимости, отличном от предусмотренных в таблице А.2, значение P находят путем линейной интерполяции.

В случае, если при проверке нормальности распределения результатов наблюдений группы для критерия 1 выбран уровень значимости q₁, а для критерия 2 - q₂, то результирующий уровень значимости составного критерия .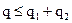

В случае, если хотя бы один из критериев не соблюдается, то считают, что распределение результатов наблюдений группы не соответствует нормальному.

Таблица А.2 - Значение p для вычисления z_p/2

n	m	q2%
		1 %	2 %	5 %
		0,98	0,98	0,96
11-14		0,99	0,98	0,97
15-20		0,99	0,99	0,98
21-22		0,98	0,97	0,96
		0,98	0,98	0,96
24-27		0,98	0,98	0,97
28-32		0,99	0,98	0,97
33-35		0,99	0,98	0,98
36-49		0,99	0,99	0,98

Приложение Б

(справочное)

Исключение грубых погрешностей результатов наблюдений

Таблица Б.1 - Значение коэффициента t для случайной величины Y, имеющей распределение Стьюдента с n-1 степенями свободы

n-1	P=0,95	P=0,99	n-1	P=0,95	P=0,99
	3,182	5,841		2,120	2,921
	2,776	4,604		2,101	2,878
	2,571	4,032		2,086	2,845
	2,447	3,707		2,074	2,819
	2,365	3,499		2,064	2,797
	2,306	3,355		2,056	2,779
	2,262	3,250		2,048	2,763
	2,228	3,169		2,043	2,750
	2,179	3,055	¥	1,960	2,576
	2,145	2,977

Таблица Б.2 - Значение коэффициента b

Объём выборки	Предельное значение b при уровне значимости a = 1-P
	0,01	0,05
	1,15	1,15
	1,42	1,46
	1,60	1,67
	1,73	1,82
	1,83	1,94
	1,91	2,03
	1,98	2,11
	2,03	2,18
	2,13	2,29
	2,21	2,37
	2,28	2,44
	2,34	2,50
	2,38	2,56

Приложение В

(справочное)

Определение аргумента функции Ф(х)

Таблица В.1-Таблица значений функции ×dZ

х	Ф(х)	х	Ф(х)	х	Ф(х)	х	Ф(х)
1,96 1,98 2,00 2,02 2,04 2,06 2,08 2,10 2,12 2,14 2,16 2,18	0,4750 0,4761 0,4772 0,4783 0,4793 0,4803 0,4812 0,4821 0,4830 0,4838 0,4846 0,4854	2,20 2,22 2,24 2,26 2,28 2,30 2,32 2,34 2,36 2,38 2,40 2,42	0,4861 0,4868 0,4875 0,4881 0,4887 0,4893 0,4898 0,4904 0,4909 0,4913 0,4918 0,4922	2,44 2,46 2,48 2,50 2,52 2,54 2,56 2,58 2,60 2,62 2,64 2,66	0,4927 0,4931 0,4934 0,4938 0,4941 0,4945 0,4948 0,4951 0,4953 0,4956 0,4959 0,4961	2,68 2,70 2,72 2,74 2,76 2,78 2,80 2,82 2,84 2,86 2,88 2,90	0,4963 0,4965 0,4967 0,4969 0,4971 0,4973 0,4974 0,4976 0,4977 0,4979 0,4980 0,4981

Приложение Г

(рекомендуемое)

Пример выполнения задания по обработке результатов прямых измерений

Произвести оценку результата измерения напряжения по результатам 25 наблюдений с помощью милливольтметра, имеющего предел основной приведенной погрешности g=1 %. Шкала применяемого прибора равномерная. Нулевая отметка находится на краю шкалы. Конечное значение диапазона измерения C_N=50 мВ. Известные систематические погрешности исключены. Неисключенные систематические погрешности измерительного прибора определяются пределом допускаемой абсолютной погрешности. Задачу решить для заранее выбранного уровня значимости q₁/2=5 %, q₂=5 %. Статистическую обработку результатов наблюдений выполнить для доверительной вероятности Р=0,95.

Таблица Г.1 – Результаты наблюдений

n
А, мВ		20,5	19,5	19,5	20,5	20,5	19,5		20,5	20,5	20,5	20,5	19,5

Продолжение таблицы Г.1

n
А, мВ		19,5	19,5	19,5	20,5			19,5	20,5	19,5	19,5	20,5

Статистическую обработку результатов наблюдений (таблица 1) выполняли по [5] для доверительной вероятности Р=0,95.

Вычисление среднего арифметического исправленных результатов наблюдений, принимаемое за результат измерения :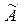

,

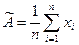где x_i- i-й результат наблюдения.

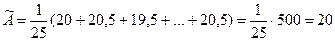
Вычисление оценки среднего квадратического отклонения (СКО) результата наблюдения

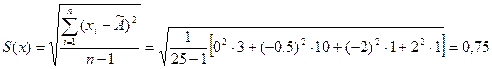
Среднее квадратичное отклонение 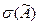результата измерения оцениваем по формуле

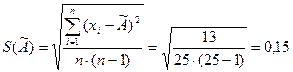
Проверка гипотезы о том, что результаты наблюдений принадлежат нормальному распределению, производим по составному критерию.

Критерий 1.

Вычисляем отношение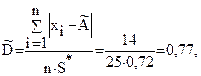

где 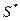- суммарная оценка СКО, вычисляемая по формуле

.

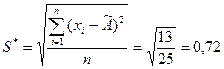Первый критерий удовлетворяется, если

,

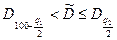где 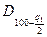и 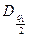- квантили распределения, получаемые из таблицы [5] по данным n, q₁/2 и (100-q₁/2), причем q₁ – заранее выбранный уровень значимости: q₁/2 = 5 %, 100-q₁/2=95 %.

Т.к. 0,7337 < 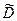=0,77<0,8637, то первый критерий удовлетворяется.

Критерий 2.

Можно считать, что критерий 2 удовлетворятся, если не более m разностей 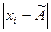превзошли значение 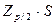. Здесь S – оценка СКО результата наблюдения, 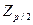- верхняя квантиль распределения нормированной функции Лапласа, отвечающая вероятности Р/2. Значение m выбирают из таблицы в зависимости от числа наблюдений n=25 и принятого уровня значимости q₂=5 %. В данном случае m=2.

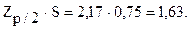
Анализ показывает, что только две разности |18-20| и |22-20|, равные 2, превзошли 1,63.

Итак, оба критерия соблюдаются, и распределение результатов наблюдений соответствует нормальному закону.

Для исключения грубых погрешностей из результатов наблюдений строим возрастающий вариационный ряд чисел:

18£19,5£19,5£19,5£19,5£19,5£19,5£19,5£19,5£19,5£19,5£20£20£20£20,5£20,5£20,5£20,5£20,5£20,5£20,5£20,5£20,5£20,5£22.

Крайние числа проверяем на анормальность. Критерием анормальности служит соотношение между

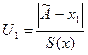и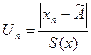

где х₁ и х_n – первый и последний члены ряда, и значением b, которое для данного n и принятой вероятности a=1-Р(u_n³b) берут из таблицы.

Так как 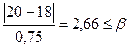и ,

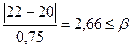то результаты наблюдений 18 и 22 мВ не являются анормальными.

Доверительные границы e (без учета знака) случайной погрешности результата находим по формуле

.

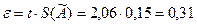Доверительные границы неисключенной систематической погрешности результата измерения принимаем в соответствии с условием задачи:

.

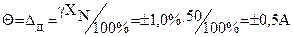Так как отношение 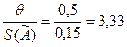, т.е. 0,8<3,33<8, то границу погрешностей результата измерения вычисляем по формуле

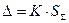, где ,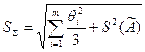

а коэффициент

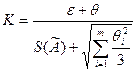, причем .

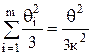Если Р=0,95, то к=1,1.

Тогда абсолютная погрешность результатов измерения

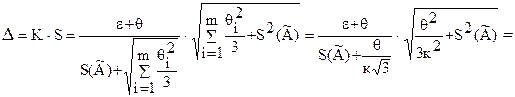
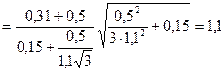(мВ).

Результат измерения: (20,0±1,1) мВ; Р=0,95; n=25.