Обучение нечетких систем на основе нейронных сетей и генетических алгоритмов.

Обучение на основе генетических алгоритмов применимо для нечеткой модели выбора операторов агрегирования информации, то есть когда при оценке поступающей в систему информации возникают ситуации, когда оценка находится “между” соседними значениями 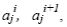, причем пользователь может говорить, что она более близка, например, к 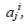, чем к 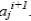. Напомним, что в рамках нечеткого подхода также предполагается, что известны значения на некоторых наборах значений . Эта информация представляется в виде логических высказываний вида “Если 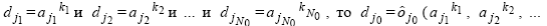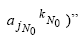для всех известных наборов 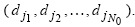. Кроме этого, предполагается, что ОАИ является монотонным, коммутативным и ассоциативным (то есть имеет смысл обобщенных операций “И”, “ИЛИ”). В рамках теории нечетких множеств эти операторы в наиболее общем виде выражаются через t - нормы (“И”) и t - конормы (“ИЛИ”) [5]. Таких t - норм и t - конорм бесконечно много. Какую из них взять в качестве оператора агрегирования, снимающего противоречие в системе?

Предлагается для выбора такого оператора использовать процедуру обучения на основе генетических алгоритмов

Наиболее активно процедуры обучения используются при разработке нечетких контроллеров [5], то есть аппаратно реализованных систем правил нечеткого логического вывода. Обучение производится путем коррекции по определенным правилам функций принадлежности используемых нечетких переменных.

В качестве параметра обучения использовать не функции принадлежности, а параметры t - норм и t - конорм. В качестве средства ее решения было предложено использовать генетические алгоритмы .

Для оценки реализуемости такой процедуры обучения была разработана система, описание которой приводится ниже.

Возьмем в качестве параметрической t-нормы строгую архимедову t-норму:

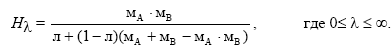
В частных случаях имеем известные в рамках теории нечетких множеств формализации операции пересечения :

Для вычисления выхода системы правил используется строгая архимедова t-конорма:

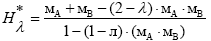
Для дефазификации выхода системы правил возьмем метод нахождения центра тяжести композиции t-нормы и t-конормы, наиболее часто используемый и самый типичный.

Для поиска параметров первоначально был опробован классический генетический алгоритм.

Хромосомы – бинарные строки, представляющие двоичный код вещественных параметров, размерности 32*(R+1) (по числу битов отвечающих за параметр на число правил в системе и один параметр t-конормы). Был реализован одноточечное скрещивание, оставляющее двух потомков, и мутация – бинарный код случайного вещественного числа, лежащего в области определения параметра. Функция пригодности вычислялась как среднеквадратичная ошибка, определяемая расстоянием между выходом контроллера и Y^* - выходом обучающей выборки выходом:

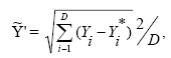
где D - размерность выборки.

При экспериментах с программой возникали ситуации ее непозволительно долгой (до нескольких часов) работы или не достижении требуемой ошибки. Для оптимизации стандартного генетического алгоритма было опробовано усиление мутации (как увеличение ее вероятности, так и разрешение мутации не в одном, а в нескольких генах хромосомы), выживание только одного потомка скрещивания их комбинации. Однако это практически не повлияло на его сходимость.

Было предпринято изменение самого принципа кодирования данных. Использовалось кодирование, отражающее структуру пространства поиска - представление хромосомы, как массива вещественных чисел размерности R+1 (параметры t-нормы каждого правила и параметр t-конормы). Это повлекло за собой необходимость разработать соответствующие операторы рекомбинации.

Мутация была реализована как получение случайного числа принадлежащего области определение параметра λ (от 0 до ∞). Вероятность мутации просчитывалась для каждой хромосомы популяции.

В качестве аналога скрещивания использовался новый оператор - “почкование”, включающий в себя следующие этапы:

1. выбор случайного числа близкого к гену “родительской” хромосомы (около 10% от величины самого числа);

2. повторение первого шага для каждого гена хромосомы.

В качестве оператора отбора использовался простой (не элитный) пропорциональный отбор по функции качества.

Шаг:

1. В новом поколении с вероятностью воспроизведения, рассчитанной оператором отбора, воспроизводятся дубликаты лучших хромосом и генерируются хромосомы, полученные почкованием и мутацией.

2. Проверяется “качественность” - минимальная среднеквадратичная ошибка хромосомы – для каждой хромосомы популяции.

3. Отмирают “неприспособленные” индивидуумы популяции.

4. Если качество лучшей хромосомы популяции удовлетворяет запросам задачи, то лучшая хромосома и является решением задачи - гены ее составляющие являются параметрами искомой t-нормы.

Иначе шаг алгоритма повторяется.