Двоичная система счисления
Цифровые логические устройства
Цель работы:изучение двоичной системы исчисления; знакомство с работой логических устройств: «НЕ», «И-НЕ», триггера и параллельного регистра.
Приборы и принадлежности: лабораторные макеты.
Литература
1. [1], § 3.1.
2. [2], § 155.
Вопросы входного контроля
1. Общий вид записи числа.
2. Способы перевода чисел десятичной системы в двоичную (уметь записать в двоичной системе числа до 20).
3. Как условно изображается инвертор?
4. Пусть на входе инвертора действует высокий уровень сигнала (логическая единица). Какой уровень сигнала на выходе инвертора?
5. Как называется логический элемент, реализующий логическую функцию «И»?
6. Составить таблицу состояний конъюнктора.
7. Как называется логический элемент, реализующий логическую функцию «ИЛИ»?
8. Составить таблицу состояний дизъюнктора.
Введение
Обработка, передача и отображение информации в медицинской аппаратуре часто производится в цифровой форме. Принцип построения и работы устройств, предназначенных для выполнения этих задач, основывается на виде системы счисления – способе записи чисел цифровыми знаками. Известны так называемые позиционные системы счисления, в которых значение каждой входящей в число цифры зависит от ее положения в записи числа. Количество различных цифр, применяемых в позиционной системе, называют основанием системы. Различают следующие системы счисления: десятичная – с основанием 10, двоичная – с основанием 2 и др. Например, любое целое число А может быть представлено в таком виде:
| |||
 | |||
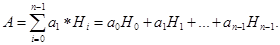Здесь n – число знаков в числе; i – номер разряда;
a1 – цифра в разряде i; Hi – вес разряда.
Совокупность цифр an-1, an-2, …, a1, a0 составляет код числа в заданной системе счисления.
Двоичная система счисления
В цифровой технике наибольшее распространение получила двоичная система счисления, содержащая только цифры 0 и 1, а ее основанием является число 2. В двоичной системе любое число обозначается цифрами 0 и 1, которые располагаются в порядке возрастания разрядов справа налево (как и в десятичной). Каждый вес разряда соответствует основанию системы в степени на единицу меньшей порядка разряда:
Нi = ri, где r-основание СС. Тогда
А =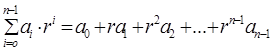 
.
Порядок записи чисел в двоичной системе счисления рассмотрим на конкретном примере. Пусть требуется записать в двоичной системе счисления число А, равное 50. Для этого нужно выполнить следующие действия.
Последовательно делим на основание системы до тех пор, пока не получим 0. Остатки дадут цифры числа:
 |
50 2
 |
50 25 2 
 |
0 24 12 2
|
 |
1 12 6 2
 |  |
0 6 3 2
|
 |
0 2 1 2
 |
 |
1 0 0
|
1
|
Меняем местами разряды (читаем справа налево), получаем:
5010 =1100102
Именно так производится перевод чисел в ПК.
На аппаратном уровне в ИМС шифраторов-дешифраторов используются сплошные логические схемы.
Для примера можно привести схему дешифратора 155ИД1.
Таким образом, число 50 в двоичной системе счисления может быть записано следующим образом:
Hi
 |
50 = 1*25+1*24+0*23+0*22+1*21+0*20 = 110010
Ai
1.2. Логическая функция «И-НЕ»
Логическая функция Y нескольких переменных (X0, X1, …, Xn-1) определяет характер логических операций, в результате которых набору входных переменных х0, х1, …, хn-1 ставится в соответствие переменная Y, т.е.
Y= f(X0, X1, …, Xn-1).
Например, логическая функция «И», как функция логического умножения, выражается зависимостью
Y=X1*X2.
Логическая функция «И-НЕ» является инверсной относительно функции «И» и выражается как
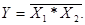
Логические функции наиболее наглядно характеризуются таблицей, в строках которой каждой комбинации входных переменных Х соответствует значение выходной переменной Y:
Таблица 1
| Х1 | Х2 | Y=X1*X2 |  |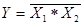
Как видно из табл.1, функция «И-НЕ» принимает значение логического «0» только при равенстве 1 всех переменных.
Тактируемый D-триггер
Условное обозначение тактируемого D-триггера показано на рис.1.
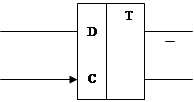
Q
Q
 |
Рис. 1.
Он имеет информационный вход D и вход синхронизации С. Если уровень сигнала на входе С=0, то состояние триггера устойчиво и не зависит от уровня сигнала на информационном входе D (режим хранения информации). При подаче на вход синхронизации С импульса информация на прямом выходе Q будет повторять информацию, подаваемую на вход D (режим записи информации).