Многократные прямые измерения
Общая последовательность обработки результатов измерений в соответствии с ГОСТ 8.207 состоит из следующих этапов.
Этап 1. Вычисление среднего арифметического значения 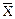 по формуле (3.2).
по формуле (3.2).
Этап 2. Расчет среднего квадратического отклонения s по формуле (3.3).
Этап 3. Проверка наличия грубой погрешности в результатах (см. выше). Если она обнаружена, то этот результат следует отбросить и повторить этапы 1 и 2.
Этап 4. Проверка соответствия результатов измерений закону нормального распределения (см. ниже).
Этап 5. Вычисление среднего квадратического отклонения  среднего арифметического по формуле
среднего арифметического по формуле
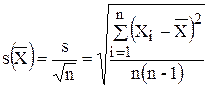 (3.4)
(3.4)
Этап 6. Определение коэффициента Стьюдента tp при заданном значении доверительной вероятности Р и числе результатов измерений n по табл. 1.5.
Этап 7. Определение доверительных границ случайной погрешности e при заданном значении доверительной вероятности Р по формуле
 (3.5)
(3.5)
Этап 8. Определение границ неисключенной систематической погрешности q результата измерения по формуле.
 (3.6)
(3.6)
где m - число составляющих погрешности
Неисключенная систематическая погрешность образуется из составляющих, в качестве которых могут быть неисключенные систематические погрешности метода, средств измерений, субъективные погрешности. Эти составляющие погрешности находят нестатистическими методами.
Этап 9. Вычисление доверительных границ погрешности результата измерений D. Данная операция осуществляется путем суммирования случайной составляющей погрешности e и неисключенной систематической составляющей погрешности q. При этом вычисляют отношение
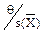 и в зависимости от полученного значения определяют погрешность результата измерения D по правилам, изложенным в табл. 3.2.
и в зависимости от полученного значения определяют погрешность результата измерения D по правилам, изложенным в табл. 3.2.
Таблица 3.2
Определение погрешности результата измерения D
Значение 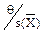 | Погрешность результата измерения D |
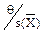 <0,8 <0,8 | D = e |
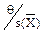 >8 >8 | D = q |
0,8£ 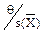 £8 £8 | 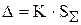 где К – коэффициент, зависящий от соотношения случайной и неисключенной систематической погрешностей, SS - оценка суммарного среднего квадратического отклонения результата измерения К и SS рассчитывают по формулам где К – коэффициент, зависящий от соотношения случайной и неисключенной систематической погрешностей, SS - оценка суммарного среднего квадратического отклонения результата измерения К и SS рассчитывают по формулам 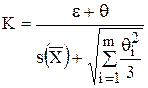 ; ; 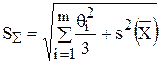 |
Этап 10. Запись результата измерений с учетом правил округления в виде
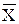 ± D при доверительной вероятности Р и числе измерений n.
± D при доверительной вероятности Р и числе измерений n.
Пример. Необходимо произвести обработку результатов измерений сопротивлений катушки сопротивления при заданной доверительно вероятности Р=0,95. Значения сопротивления Хi (МОм) приведены в табл. 3.3. Погрешность средства измерения равна ±1 МОм.
Таблица 3.3
Результаты измерений и вычислений
| № | Хi | Хi- 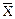 |  |
| -1,7 | 2,89 | ||
| -0,7 | 0,49 | ||
| 3,3 | 10,89 | ||
| 0,3 | 0,09 | ||
| -2,7 | 7,29 | ||
| 6,1 | 37,21 | ||
| -3,7 | 13,69 | ||
| -2,7 | 7,29 | ||
| 1,3 | 1,69 | ||
| 2,3 | 5,29 | ||
 | 391,9 | 86,82 |
Решение. По формулам (3.2) и (3.3) вычислим среднее арифметическое значение и среднее квадратическое отклонение
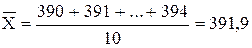 МОм
МОм
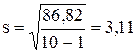 МОм
МОм
Проверим, имеется ли в результатах грубая погрешность (Хсомн=398). По формуле (3.1) вычислим b
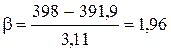
При a=0,05 и n=10 bт=2,414. b<bт, следовательно, грубых погрешностей в результатах нет.
Вычислим 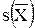 по формуле (3.4).
по формуле (3.4).
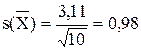 МОм
МОм
Для Р=0,95 и n=10 коэффициент Стьюдента tр = 2,26 (табл. 1.5).
По формуле (3.5) находим доверительную границу случайной погрешности:

Имеется одна составляющая неисключенной погрешности (погрешность средства измерения), т.е. m=1. Следовательно, граница неисключенной систематической погрешности q=1 МОм
Вычислим отношение
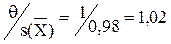
В соответствии с правилами, указанными в табл. 3.2, погрешность результата измерения D составляет
 2,34
2,34
Запишем результат измерений, учитывая рекомендации по округлению: (391,9 ± 2,3) МОм при Р=0,95 и n=10.
