Рассмотрим практическое применение изложенного материала.

Перечень базисов.

1. 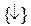- базис Пирса (элемент Вебба);

2. 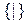- базис Шеффера;

3. - коипликация, эквиваленция;

4. 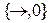- импликативный базис;

5. - импликация, коимпликация;

6. - импликация, сложение по модулю 2;

7. - коимпликативный базис;

8. - импликативный базис;

9. - конъюнктивный базис Буля;

10. - дизъюнктивный базис Буля;

11. - коимпликативный базис (коимпликация, константа 1);

12. - эквиваленция, конъюнкция, константа 0;

13. - эквиваленция, дизъюнкция, константа 0;

14. - сложение по модулю 2, конъюнкция, эквиваленция;

15. - сложение по модулю 2, дизъюнкция, эквиваленция;

16. - базис Жегалкина;

17. - сложение по модулю 2, дизъюнкция, константа 1.

Базис минимальный, если удаление хотя бы одной функции превращает систему ФАЛ в неполную.

Проблема простейшего представления логических функций сводится к выбору не только базиса, но и формы наиболее экономного представления этих функций.

Если сравнить в смысле минимальности различные формы представлений ФАЛ, то станет ясно, что нормальные формы экономичнее совершенных нормальных форм, но с другой стороны, нормальные формы не дают однозначного представления.

Минимальная (тупиковая) форма представления ФАЛ содержит минимальное количество термов и переменных в термах , дальнейшие упрощения минимальной формы не возможны.

Дисциплина «Методы логического проектирования»рассматривает теоретические аспекты минимизации логических функций. Методов минимизации несколько. Перечислим основные: Метод неопределённых коэффициентов для базиса И- ИЛИ - НЕ, метод Квайна, метод минимизирующих карт и т.д. Подробно каждый из методов рассмотрен в пособии А.Я. Савельева «Основы информатики».

Упрощение сложных логических выражений может быть осуществлено по основным законам и аксиомам, изложенным выше.

Пример.

Пусть задана логическая функция с помощью таблицы истинности:F(a,b,c) = A9₁₆.

Представить её в базисе Жегалкина, используя не более 4 - х элементов.

Решение.

A	B	c	F
				*
				*
				*
				*

Построим СДНФ для заданной функции.

Так как задан базис Жегалкина, целесообразно элементарные минтермы соединить операцией сложение по модулю 2.

СДНФ: a b c ⊕ ab c ⊕ a b c ⊕ abc.

Упростим полученную формулу:

a b c ⊕ ab c ⊕ a b c ⊕ abc = a c(b ⊕ b) ⊕ a (b c ⊕ bc) = a c ⊕ a(b~c) = a c ⊕ a(b ⊕ c) = a c ⊕ ab ⊕ a c = c(a⊕ a) ⊕ ab = c ⊕ ab =

c ⊕ ab⊕1.

Рассмотрим практическое применение изложенного материала.

Задача 1. На вопрос, кто из трех студентов изучал логику, был получен следующий ответ: если изучал первый, то изучал и второй, но неверно, что если изучал третий, то изучал логику и второй. Кто из студентов изучал логику?

Решение.

Обозначим через В₁, В₂, В₃ высказывания, состоящие в том, что соответственно первый, второй, третий студенты изучали логику. Из условия задачи следует истинность высказывания:

(В₁ → В₂) & ( )

Так как В₁ → В₂ = ₁ + В₂ и = В₃ & ₂, получаем следующее выражение:

( ₁ & В₂) (В_{3 2}) = _{1 2} В₃ & В_{2 2} В₃ = _{1 2} В₃

Из полученного выражения следует, что логику изучал третий студент.

Задача 2. Алеша, Боря и Гриша нашли в земле сосуд. Рассматривая находку, каждый высказал по два предложения:

Алеша: это сосуд греческий и изготовлен в 5-ом веке.

Боря: это сосуд финикийский и изготовлен в 3-ем веке.

Гриша: это сосуд не греческий и изготовлен в 4-ом веке.

Каждый из них оказался прав только в одном из предположений. Где и в каком веке изготовлен сосуд?

Решение.

Примем следующие обозначения:

G – сосуд греческий;

F – сосуд финикийский;

V₃ – сосуд изготовлен в 3-ем веке;

V₄ – сосуд изготовлен в 4-ом веке;

V₅ – сосуд изготовлен в 5-ом веке;

Формализуем условие задачи, используя приведенные выражения:

Высказывание Алеши G ₅ ˅ V₅ = 1.

Высказывание Бори F ₃˅ V₃ = 1.

Высказывание Гриши ₄ ˅ G V₄ =1 (так как каждый был прав только в одном предположении из двух)

Полученные высказывания логически перемножаем (так как высказывался Алеша, Боря и Гриша), результат должен быть равен 1, т.е.

(G ₅ ˅ V₅) (F ₃ ˅ V₃) ( ₄ ˅ G V₄)

Выполним умножение по действиям:

1) (G ₅ ˅ V₅) (F ₃ ˅ V₃) = G ₅ F ₃ ˅ G ₅ V₃ ˅ V₅ F ₃ ˅ V₅ V₃;

Конъюнкция G ₅ F ₃ = 0, т.к. не могут быть одновременно две страны.

Конъюнкция V₅ V₃ = 0, т.к. не могут быть одновременно 3-й и 5-й века.

В итоге получаем после умножения первых двух скобок: G ₅ V₃ ˅ V₅ F ₃

2) (G ₅ V₃ ˅ V₅ F ₃) ( ₄ + G V₄) = G ₅ V_{3 4} + V₅ F ₃ G V₄ +

+ V₅ F _{3 4} + G ₅ V₃ G V₄ = 1

Конъюнкции: G ₅ V_{3 4}, G ₅ V₃ G V₄, V₅ F ₃ G V₄ равны нулю.

В итоге получаем: V₅ F _{3 4} = F _{3 4} V₅ = 1, т.е. сосуд финикийский, изготовлен в 5-ом веке.

Если обратить внимание на то, что первое и второе высказывание можно записать используя операцию сложение по модулю 2, а третье высказывание – это эквиваленция, мы приходим к более простым формулам и преобразованиям:

(G ⊕ V₅) (F ⊕ V₃) (G ~ V₄) = (G ⊕ V₅) (F ⊕ V₃) ( ⊕ V₄) = 1

Упростим данное выражение:

(G ⊕ V₅) (F ⊕ V₃) = G F ⊕ G V₃ ⊕ F V₅ ⊕ V₅ V₃

Конъюнкции G F и V₅ V₃ равны нулю.

(G V₃ ⊕ F V₅) ( ⊕ V₄) = G V₃ ⊕ G V₃ V₄ ⊕ F V₅ ⊕ F V₅ V₄ = 1

Конъюнкции G V₃ , G V₃ V₄, F V₅ V₄ равны нулю, следовательно остается конъюнкция F V₅ , т.е. сосуд финикийский, 5-й век.