Система стабилизации положения обратного маятника с линеаризацией в нескольких рабочих точках

Цель работы: ознакомиться с особенностями, методикой создания и принципом действия систем нечеткой логики типа Сугено на примере системы стабилизации положения обратного маятника.

Задание

1. Собрать модель обратного маятника. Убедиться в адекватности ее работы.

2. Создать математическое описание данной модели в пространстве состояний и линеаризовать его в трех рабочих точках – 0, 15 и 30º. Для каждого полученного набора матриц состояния синтезировать модальный регулятор.

3. Подключить регулятор, синтезированный для угла 0º, к модели обратного маятника. Пронаблюдать графики переходных процессов при следующих значениях начального угла отклонения: 1, 5, 10, 15, 20, 30º.

4. Создать систему нечеткой логики для плавного переключения между полученными регуляторами. Сравнить качество работы системы для полученных ранее случаев.

Таблица 7.1 – Варианты индивидуального задания

№ вар.
l, м	0.5	0.7	0.9	1.1	1.3	1.5	1.7	1.9	2.1	2.3
m, кг		1,3	1,6	1,9	2,2	2,5	2,8	3,1	3,4	3,7
M, кг		3,5		4,5		5,5		6,5		7,5

№ вар.
l, м	0.5	0.7	0.9	1.1	1.3	1.5	1.7	1.9	2.1	2.3
m, кг	1,2	1,5	1,8	2,1	2,4	2,7		3,3	3,6	3,9
M, кг	3,2	4,2	5,2	6,2	7,2	8,2	9,2	10,2	11,2	12,2

№ вар.
l, м	0.5	0.7	0.9	1.1	1.3	1.5	1.7	1.9	2.1	2.3
m, кг	1,1	1,4	1,7		2,3	2,6	2,9	3,2	3,5	3,8
M, кг	3,7	4,7	5,7	6,7	7,7	8,7	9,7	10,7	11,7	12,7

№ вар.
l, м	0.5	0.7	0.9	1.1	1.3	1.5	1.7	1.9	2.1	2.3
m, кг		4,3	4,6	4,9	5,2	5,5	5,8	6,1	6,4	6,7
M, кг	10,5	11,5	12,5	13,5	14,5	15,5	16,5	17,5	18,5	19,5

№ вар.
l, м	0.5	0.7	0.9	1.1	1.3	1.5	1.7	1.9	2.1	2.3
m, кг	4,15	4,45	4,75	5,05	5,35	5,65	5,95	6,25	6,55	6,85
M, кг

Лабораторная работа №8

Адаптивные системы нечеткой логики

Цель работы: ознакомиться с возможностями реализации адаптивных систем нечеткой логики в программном пакете Matlab.

Задание

1. По вариантам задания из л.р. №11 создать вектора аргумента и значения указанной нелинейной функции в заданном пределе, состоящие из 20 точек.

2. Создать адаптивную систему нечеткой логики, обучить ее на полученные вектора. Четные варианты используют метод кластеризации, а нечетные – разбиение пространства. Проверить точность работы полученной системы при отработке вектора входных значений, содержащего 100 и 500 элементов.

3. Обучить систему на вектор из 100 элементов, сравнить полученные результаты.

№ вар.	Функция	Диапазон для аппроксимации
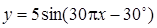		[0…0.1]
		[0…0.65]
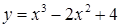		[-2…3]
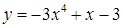		[-1.5…2]
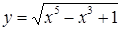		[-1.2…3]
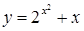		[-1,5…1,5]
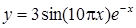		[0…0.3]
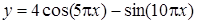		[-0,5…-0,1]
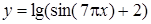		[-0,5…0]
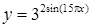		[-0,2…0]
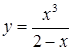		[-2…1,2]
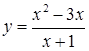		[-0,5…4]
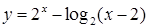		[2,5...7]
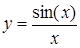		[2…11]
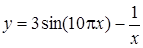		[0,6…0,9]
№ вар.	Функция	Диапазон для обучения
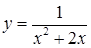		[0,5…2,5]
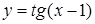		[-0.5…2,5]
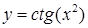		[0.2…1]
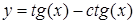		[-1,4…-0,3]
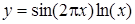		[1…2]
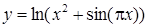		[0,5…2]
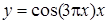		[0…1]
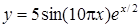		[-0,5…-0,1]
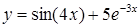		[-0,5…2]
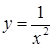		[-1,5…1,5]
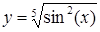		[0…2]
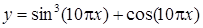		[0…0,2]
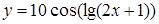		[-0.4…5]
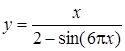		[1…1,5]
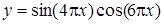		[0,5…1]
		[-1…1]
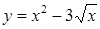		[0,5…2]
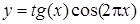		[-1…1]
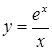		[0,5…2]
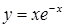		[0,6…1,6]
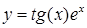		[-1…1]
		[-0,5…0,5]
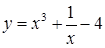		[0,4…1,4]
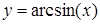		[-1…1]
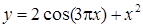		[-1…0]
		[0.1…2]
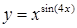		[1…2]
№ вар.	Функция	Диапазон для обучения
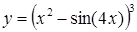		[0…1,5]
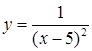		[4…6]
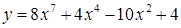		[-3…3]
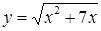		[0…10]
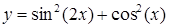		[-4…-1]
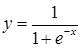		[-3…3]
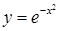		[-1,5…1,5]
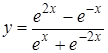		[-3…3]

Указания к выполнению работы

Графики, полученные в п.п. 2 и 3 следует строить следующим образом. В одном графическом окне, в разных системах координат строятся графики непосредственно функций (исходный массив – маркерами) и ошибки аппроксимации (для этого необходимо использовать массив с наибольшим количество элементов, т.е. для пункта 2 – 100 и 500 точек, для п. 3 – 500 точек).

Кроме того для пункта №3 необходимо извлечь данные об аппроксимирующих функциях и наложить их на график исходной функции, построенный в новом графическом окне.

Для п.п. 2 и 3 кроме того необходимо получить графики функций принадлежности входной координаты.