Формулы алгебры высказываний

С помощью логических операций над высказываниями можно строить различные, более сложные высказывания. Определим понятие формулы алгебры высказываний.

Формулой алгебры высказываний (формулой) называется

1) любое высказывание (высказывательное переменное);

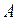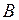2) если и – формулы, то 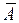, , 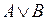, , 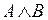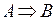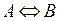– тоже формулы;

3) кроме формул приведенных в п.п 1) и 2) других формул в алгебре высказываний нет.

Если формула 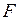образована, например, из формул (переменных) 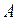, 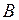и 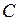, то используем следующую запись: .

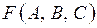Две формулы 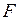и 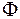, образованные из одних и тех же переменных, называются равносильными, если на одинаковых наборах значений входящих в них переменных они принимают одинаковые логические значения и обозначается .

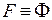Формула называется тавтологией (тождественно истинной), если она принимает только истинное значение на всех наборах значений входящих в неё переменных.

Формула называется противоречием (тождественно ложной), если она принимает только ложное значение на всех наборах значений входящих в неё переменных.

Формула называется выполнимой, если она не является ни тавтологией и ни противоречием.

Для того, чтобы формулы 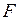и 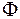, образованные из одних и тех же переменных являлись равносильными, необходимо и достаточно, чтобы формула 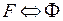являлась тавтологией.

Основные тавтологии

Приведем перечень равносильных формул и названий некоторых из них:

1. 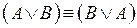– коммутативность дизъюнкции;

2. 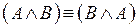– коммутативность конъюнкции;

3. 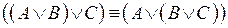– ассоциативность дизъюнкции;

4. 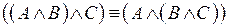– ассоциативность конъюнкции;

5. 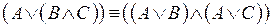– дистрибутивность дизъюнкции относительно конъюнкции;

6. 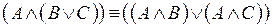– дистрибутивность конъюнкции относительно дизъюнкции;

7. 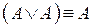– идемпотентность дизъюнкции;

8. 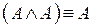– идемпотентность конъюнкции;

9. 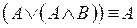– первый закон поглощения;

10. 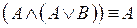– второй закон поглощения;

11. ;

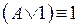12. ;

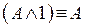13. ;

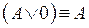14. ;

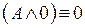15. 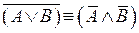– первый закон де Моргана;

16. 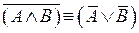– второй закон де Моргана;

17. 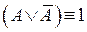– закон исключённого третьего;

18. 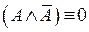– закон противоречия;

19. 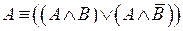– первая формула расщепления;

20. 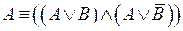– вторая формула расщепления;

21. 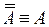– закон снятия дойного отрицания;

22. 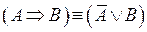– формула, представляющая импликацию через отрицание и дизъюнкцию;

23. 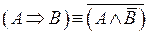– формула, представляющая импликацию через отрицание и конъюнкцию;

24. 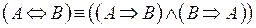– формула, представляющая эквиваленцию через импликацию и конъюнкцию;

25. 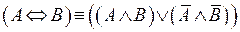– первая формула, представляющая эквиваленцию через отрицание, дизъюнкцию и конъюнкцию;

25. 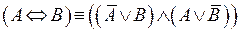– вторая формула, представляющая эквиваленцию через отрицание, дизъюнкцию и конъюнкцию.

Приведем две равносильные формулы, используемые в разделе ДНФ и КНФ:

26. 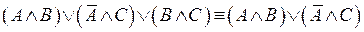– первое правило Блейка;

27. 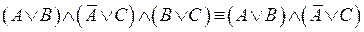– второе правило Блейка.

Справедливость этих равносильных формул можно проверить построив их таблиц истинности.

Если в этих равносильных формулах символ 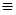заменить символом 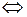, то получаются тавтологии, называемые основными.

Нормальные формы

Пусть

(*)

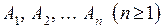– высказывательные переменные.

Элементарной дизъюнкцией (ЭД)называется дизъюнкции любых переменных 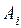из (*) или их отрицания 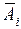. Например, если 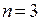и набор (*) имеет вид 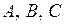, то 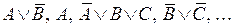– элементарные дизъюнкции. Если в элементарной дизъюнкции участвует все переменные из (*) (либо сама, либо её отрицание), то она называется полной элементарной дизъюнкцией (ПЭД). Например, в случае 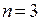, перечислим всех полных элементарных дизъюнкций: , , , , , , , .

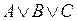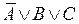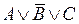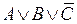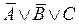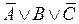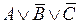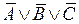Элементарной конъюнкцией (ЭК)называется конъюнкции любых переменных 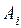из (*) или их отрицания 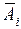. Например, если 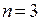и набор (*) имеет вид 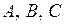, то 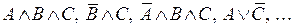– элементарные конъюнкции. Если в элементарной конъюнкции участвует все переменные из (*) (либо сама, либо её отрицание), то она называется полной элементарной конъюнкцией (ПЭК). Например, в случае 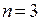, перечислим всех полных элементарных конъюнкций: , , , , , , , .

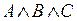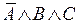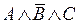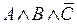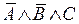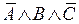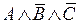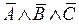Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкции произвольного количества элементарных конъюнкций. Схематично ДНФ имеет вид:

(ЭК)Ú (ЭК)Ú (ЭК)Ú … .

Если все входящие в ДНФ элементарные конъюнкции являются полными, то она называется совершенной дизъюнктивной нормальной формой (СДНФ). Схематично СДНФ имеет вид:

(ПЭК)Ú (ПЭК)Ú (ПЭК)Ú … .

Конъюнктивной нормальной формой (КНФ) называется конъюнкции произвольного количества элементарных дизъюнкций. Схематично КНФ имеет вид:

(ЭД)Ú (ЭД)Ú (ЭД)Ú … .

Если все входящие в КНФ элементарные дизъюнкции являются полными, то она называется совершенной конъюнктивной нормальной формой (СКНФ). Схематично СКНФ имеет вид:

(ПЭД)Ú (ПЭД)Ú (ПЭД)Ú … .

Для каждой формулы, не являющейся тождественно истинной и тождественно ложной, существуют равносильные СДНФ и СКНФ.

Функции алгебры логики

Функцией алгебры логики 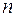переменных (функцией Буляили булевой функцией) называется функция 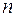переменных

,

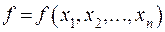где каждая переменная 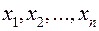принимает два значения 0 и 1: 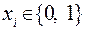, и при этом сама функция 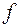может принимать только одно из двух значений 0 и 1: .

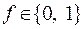Число различных булевых функций 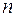переменных равно 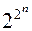. В частности, различных булевых функций одной переменной четыре, а различных булевых функций двух переменных шестнадцать. Перечислим эти функции.

Рассмотрим таблицу истинности всех различных булевых функций одной переменной:

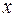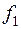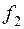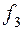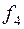Из таблицы следует, что эти функции можно представить как формулы исчисления высказываний:

.

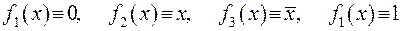Таблица истинности всех различных булевых функций двух переменных имеет вид:

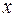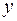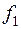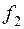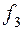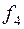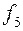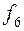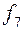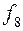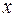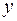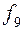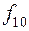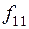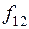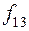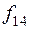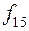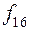Этим функциям соответствуют следующие формулы исчисления высказываний:

,

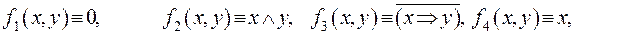
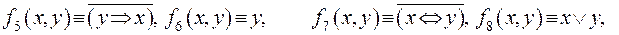
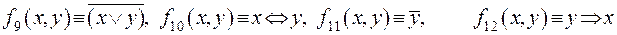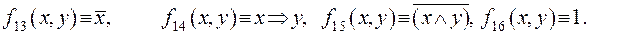
Каждой булевой функции можно сопоставить формулу алгебры высказываний. С этой целью введем обозначение

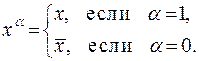
Следующий факт для булевой функции с любым количеством переменных. Приведем его для функции двух переменных.

Произвольная булева функция двух переменных 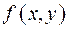представима в виде:

.

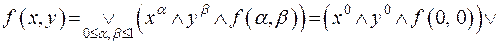
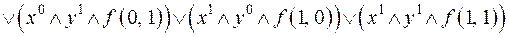Для краткости записи опустим символ конъюнкции: вместо 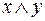будем писать :

.

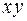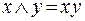Это обозначение совпадает и с содержанием этих операций: значение конъюнкции 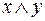, на самом деле, совпадает со значением арифметической операции умножения .

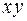Полагая 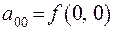, , 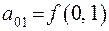, 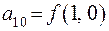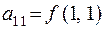функцию 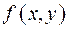можно представить следующим образом:

.

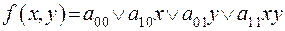Полученное представление справедливо для всех булевых функций с любым количеством переменных.

Многочлен Жегалкина

Операция арифметического умножения нами введена. Введем новую логическую операцию, называемую сложением по модулю 2. Сложение по модулю 2 обозначается 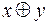. Она определяется как отрицание эквиваленции переменных 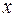и :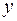

.

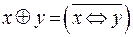Таблица значений сложения по модулю 2 имеет вид

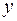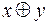Отметим некоторые свойства сложения по модулю 2:

1) ;

2) ;

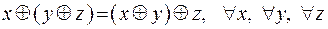3) ;

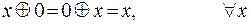4) ;

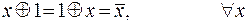5) ;

6) .

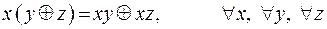Многочленом Жегалкина от 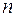переменных 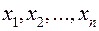называется функция, являющейся суммой произведений всевозможных одночленов, в которых все переменные входят не выше, чем в первой степени:

.

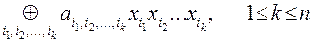Примеры.

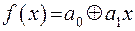– многочлен Жегалкина первой степени;

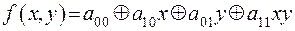– многочлен Жегалкина второй степени;

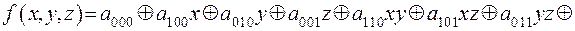
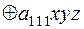– многочлен Жегалкина второй степени.

При построении многочлена Жегалкина полезно использовать следующие преобразования:

.

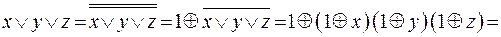
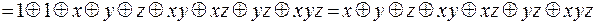Содержание

Правила выполнения и оформления контрольных работ………….
Задания для контрольных работ……………………………………..
	Задание № 1………………………………………………...
	Задание № 2………………………………………………...
	Задание № 3………………………………………………...
	Задание № 4………………………………………………...
	Задание № 5………………………………………………...
	Задание № 6………………………………………………...
	Задание № 7………………………………………………...
	Задание № 8………………………………………………...
Образцы решения и оформления заданий…………………………..
	Задание № 1………………………………………………...
	Задание № 2………………………………………………...
	Задание № 3………………………………………………...
	Задание № 4………………………………………………...
	Задание № 5………………………………………………...
	Задание № 6………………………………………………...
	Задание № 7………………………………………………...
	Задание № 8………………………………………………...
Краткий теоретический материал……….…………………………..
	1. Основные понятия теории множеств…………………..
	2. Операции над множествами……………………………
	3. Бинарное отношение……………………………………
	4. Действия над высказываниями…………………………
	5. Формулы алгебры высказываний………………………
	6. Основные тавтологии…………………………………...
	7. Нормальные формы……………………………………..
	8. Функции алгебры высказываний……………………….
	9. Многочлен Жегалкина…………………………………..