Определение разделительного силлогизма.
Разделительным называется силлогизм, в составе которого есть разделительное (дизъюнктивное) суждение. Разделительное суждение имеет структуру: «А либо В» или p 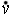 q:
q:
а) если обе посылки и заключение — разделительные суждения, то такое умозаключение называется чисто разделительным силлогизмом. Он имеет следующую структуру:
| А есть В или С |
| С есть Д или Е |
| А есть В или Д или Е |
Например:
| Четырёхугольники есть равносторонние и неравносторонние |
| Равносторонние есть квадраты или ромбы |
| Четырёхугольники есть квадраты или ромбы, или неравносторонние |
Разделительно-категорические выводы и их модусы.
если силлогизм состоит из одного разделительного и одного категорического суждения, то такой силлогизм называется разделительно–категорическим. Разделительное суждение образует бoльшую посылку, а категорическое — меньшую. Разделительно-категорический силлогизм так же, как и условно- категорический, имеет два правильных модуса:
Понендо толленс 1. Модус понендо толленс (лат. ponendo tollens) - утверждающе-отрицающий.
В нём меньшая посылка и заключение находятся в отношении альтернативы. При этом меньшая посылка утверждает одну из альтернатив, а заключение отрицает другую альтернативу. Схематически данное умозаключение выглядит следующим образом:
| S есть А , либо В | и | S есть А, либо В | ||
| S есть А | S есть В | |||
| Следовательно, S не-есть В | Следовательно, S не-есть А |
На языке исчисления предикатов они записываются так:
р 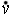 q q | р 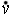 q q | |
| p | q | |
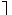 q q | 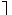 p p |
Например:
| Данное событие является случайным либо закономерным |
| Оно — случайно |
| Значит, оно не закономерно |
| Это зимняя сессия или летняя |
| Данная сессия - летняя |
| Значит, она не является зимней |
Толлендо поненс 2. Модус толлендо поненс (лат. tollendo ponens) отрицающе- утверждающий.
В нём меньшая посылка и заключение также образуют альтернативу, только теперь, наоборот, меньшая посылка отрицает одну из альтернатив, а заключение утверждает другую альтернативу. Отсюда и название – «отрицающе-утверждающий». Схематически данное умозаключение выглядит следующим образом:
| S есть А , либо В | и | S есть А, либо В | ||
| S не-есть А | S не-есть В | |||
| Следовательно, S есть В | Следовательно, S есть А |
В символической логике:
р 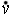 q q | р 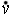 q q | |
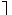 p p | 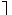 q q | |
| q | p |
Например:
| Телевизоры бывают чёрно-белыми и цветными |
| Этот телевизор не чёрно-белый |
| Значит, он — цветной |
| Данное суждение истинно или ложно |
| Оно не является ложным |
| Значит, оно истинно |
Поскольку в данном случае речь идёт об альтернативных суждениях, важно, чтобы были выявлены всевозможные альтернативы. Например:
| Ветер дует или с Севера, или с Юга, или с Востока |
| Сегодня он дует с Севера |
| Значит, он не является ни южным, ни восточным |
В данном примере проведено несоразмерное деление и выявлены не все альтернативы. Поэтому вывод может оказаться ошибочным.
Упражнения:
1. Определите фигуру, модус и правильность следующих разделительных силлогизмов:
1.1. Суждения бывают либо истинные, либо ложные. Данное суждение - истинно. Значит, оно не является ложным. Утверждающе-отрицательный модус, правильный.
1.2. Это или убийство, или несчастный случай. Это не несчастный случай. Следовательно, это - убийство. Отрицающе-утверждающий, правильный.
1.3. Он учится на дневном или заочном. Но я знаю точно, что не на дневном. Значит, на заочном.Отрицающе-утверждающий, правильный.
1.4. Умозаключение бывает непосредственным или опосредованным. Данное умозаключение - силлогизм, значит, оно не является непосредственным.Утверждающе-отрицательный модус, неправильный.
ТЕМА № 22
"Условно-разделительные силлогизмы".
План:
1.Образование условно-разделительных выводов.
2.Дилемма и её разновидности.
Образование условно-разделительных выводов.
Условно–разделительным называется силлогизм, в составе которого есть условное и разделительное суждение. Если в разделительной посылке анализируются две альтернативы, то такой условно-разделительный силлогизм называется дилеммой (от греч. di(s) — дважды и lemma — предположение). Могут быть также трилеммы, тетралеммы и др. Дилемма относится к числу часто употребляемых условно- разделительных выводов.
Дилемма и её разновидности.
Конструктивная дилемма или позитивная дилемма. Она, в свою очередь, может быть простой или сложной:
а) простая конструктивная дилемма имеет структуру:
| Если А, то С; если В, то С | или: | p → q; r → q | ||
| А или В | р 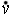 r r | |||
| С | q |
«простой» она считается за счёт условной посылки, в которой из разных оснований вытекает одно следствие;
«конструктивной» она называется, так как её заключение — утвердительное суждение;
«дилеммой» она называется, так как её меньшая посылка содержит две альтернативы. Например:
| Если он придёт в суд, то развод состоится |
| Если он не придёт в суд, то развод всё равно состоится |
| Придёт он в суд или не придёт |
| Развод все равно состоится |
б) сложная конструктивная дилемма имеет структуру:
| Если А, то В; если С, то D | или: | p → q; r → s | ||
| А или C | р 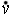 r r | |||
| B или D | q 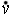 s s |
«сложной» данная дилемма называется, так как в условной посылке из разных оснований вытекают разные следствия;
«конструктивной» - так как заключение силлогизма — утвердительное суждение;
«дилеммой» - так как в меньшей посылке рассматриваются два варианта.
Например:
| Если это правильный вывод, то он даёт истинный результат, |
| а если вывод — неправильный, то результат — ложный. |
| Вывод может быть правильным либо неправильным. |
| Значит, он может быть либо истинным, либо ложным. |
2. Деструктивная дилемма или разрушительная дилемма может быть также простой или сложной:
а) простая деструктивная дилемма имеет структуру:
| Если А, то В; если А, то С | или: | p > q; p > r | ||
| не-В и не-C | 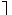 q q 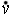 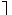 r r | |||
| Следовательно, не-А | 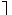 p p |
«простой» она называется, так как разные следствия вытекают из одного основания в большей условной посылке;
«деструктивной» она является, так как заключение данного силлогизма — суждение отрицательное. Оно отрицает основание условной посылки;
«дилеммой» данное умозаключение называется, так как в меньшей посылке отрицаются оба возможных следствия из основания.
Например:
| Если это простое суждение, то его связка или утвердительная, или отрицательная |
| Эта связка не является утвердительной и не является отрицательной |
| Значит, данное суждение не является простым |
б) сложная деструктивная дилемма имеет структуру:
| Если А, то В; если С, то D | или: | p > q; r > s | ||
| не-В и не-D | 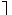 q q 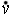 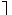 s s | |||
| Следовательно, не-А и не-С | 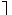 p p 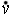 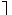 r r |
«сложной» данная дилемма называется потому, что её условная посылка содержит два разных основания и два следствия;
«деструктивной» — так как в заключении отрицаются оба основания условной посылки;
«дилеммой» — так как в меньшей посылке отрицаются оба следствия из основания.
Например:
| Если обобщить понятие, то его объём увеличится, |
| если ограничить, то его объём уменьшится |
| Объём понятия не увеличился и не уменьшился |
| Значит, понятие не обобщалось и не ограничивалось. |
Упражнения:
1. Определите вид и правильность дилеммы в следующих условно-разделительных силлогизмах:
1.1. Если это - острый аппендицит, то нужна немедленная операция. Если же это перитонит, то также нужна немедленная операция. Следовательно, острый ли это аппендицит или перитонит - нужна немедленная операция. Простая конструктивная дилемма. Правильная.
1.2. Если родится мальчик, назовем его Кирилом, а если - девочка, то назовем ее Катей. Поскольку скоро у нас родится мальчик или девочка, то у нас вскоре появится Кирилл или Катя. Сложная конструктивная дилемма. Правильная.
1.3. Если он все-таки решится приехать, то поселится, как всегда, либо в “Планете”, либо в “Юбилейной”. Но ни там, ни там его нет. Значит, передумал и не приехал.Простая деструктивная дилемма. Правильная.
1.4. Если это условный силлогизм, то в нем должна быть условная посылка, а если разделительный, то - разделительная. А поскольку ни условной ни разделительной посылки нет, то данный силлогизм не является ни условным, ни разделительным. Сложная деструктивная дилемма. Неправильная.
ТЕМА № 23
"Индуктивные умозаключения".
План:
1. Понятие недедуктивного вывода.
2. Полная и неполная индукция. Схемы вывода и достоверность обобщения.
3. Основные ошибки индуктивных выводов.
Понятие недедуктивного вывода.
Дедуктивные методы, о которых шла речь в предыдущих главах, формулируются на основе накопленного в прошлом истинного знания. Оно может принимать вид законов, принципов, общих положений. Выступая в качестве посылок правильного дедуктивного умозаключения, истинное знание служит содержательным аргументом при объяснении, обосновании, доказательстве частных случаев и формулировок. В этом смысле дедуктивные рассуждения достоверны и доказательны. Однако людям часто приходится иметь дело с иной мыслительной практикой, когда предметом мысли выступает множество, класс объектов, исследуемых с целью выявления и обобщения их общих признаков. Логической формой обобщения человеческого опыта являются недедуктивные выводы и, прежде всего, индуктивные умозаключения.
Индуктивное умозаключение можно определить в узком и широком смысле:
а) в узком смысле под индуктивным умозаключением понимают логический переход от частных посылок к общему заключению;
б) в широком смысле под индукцией понимают определенный метод научного исследования и теоретического обобщения эмпирического опыта (наблюдений, измерений, экспериментов). В силу незавершенности человеческого опыта и нерегистрируемости класса предметов, выступающих объектом индуктивного анализа, индуктивные выводы относятся к числу правдоподобных или вероятностных умозаключений.
Особенностью индуктивных выводов является то, что они основываются на таких правилах рассуждения, которые не гарантируют получение из истинных посылок всегда истинных заключений. Поэтому они являются лишь правдоподобными и имеют вероятностный характер. Иначе говоря, индукция подчиняется содержательным (в отличие от формально-дедуктивных) правилам вывода. То есть, даже если записать это правило в символическом виде, «формальным» в дедуктивном смысле оно все равно не станет. Одно и то же правило индуктивного обобщения в каждом случае требует семантической интерпретации. Поясним это на примере. Но сначала запишем общую схему индуктивного умозаключения. Каждая посылка умозаключения будет соответствовать отдельному эмпирическому случаю.
| Схема индуктивного вывода: |
| 1-й случай: S1 обладает (или не обладает) свойством Р |
| 2-й случай: S2 обладает (или не обладает) свойством Р |
| 3-й случай: S3 обладает (или не обладает) свойством Р |
| ……………………………………………………………… |
| n-й случай: Sn обладает (или не обладает) свойством Р |
| S1, S2, S3,…, Sn принадлежат классу S. |
| Все S обладают (не обладают) P. |
Теперь вернемся к нашему разговору о неформальном характере этого правила. Если бы вышеприведенная схема была схемой правильного дедуктивного вывода, то при наличии истинных посылок и, следуя этой схеме, мы бы всегда получали истинные заключения. Однако в случае индуктивного умозаключения это невозможно. Беря истинные посылки и следуя данной схеме, мы в одних случаях будем получать истинный результат, а в других – ложный. В этом «соль» индукции. Например, исследуя электропроводимость металлов, физика пришла к заключению:
| Железный стержень (S1) проводит электрический ток (P) |
| Медный стержень (S2) проводит электрический ток (P) |
| Серебряный стержень (S3) проводит электрический ток (P) |
| S1, S2, S3 – принадлежат к классу металлов (S) |
| Все металлы (S) – электропроводны (P) |
Подобным образом полученно огромное множество научных выводов, с которыми наука обращается как с истинными знаниями (закон Ньютона, закон всемирного тяготения и др.). Однако в случаях, когда обобщение делается поспешно или не по существенному признаку, а по случайному, та же схема вывода приводит к ложному заключению. Например, впервые оказавшись в африканской стране и приехав туда в «сезон дождей», можно ошибиться со следующим выводом:
| В первый день (S1) шел сильный ливень (P) | |
| Во второй день (S2) шел сильный ливень (P) | |
| В третий день (S3) шел сильный ливень (P) | |
| …………………………………………………. | |
| В n-й день (Sn) шел сильный ливень (P) | |
| В Африке каждый день идет тропический ливень. |
Полученное заключение противоречит реальному положению дел и означает ложное заключение. На самом деле нашим понятиям «зима» и «лето» соответствуют свойственные экваториальному климату понятия «сухой сезон» и «сезон дождей». Что касается оставшихся «наших» времен года («весна» и «осень»), то Африке они не известны. Там природа «просыпается» каждое утро, а урожай собирают непрерывно.
Полная и неполная индукция. Схемы вывода и достоверность обобщения.
Полная индукция - это такой вид индуктивного умозаключения, в котором вывод о принадлежности отдельного признака всему классу исследуемых предметов делается на основании установленных фактов о принадлежности данного признака каждому элементу данного класса.
| Схема полной индукции |
| 1-й элемент класса S(S1) обладает (не обладает) свойством Р |
| 2-й элемент класса S(S2) обладает (не обладает) свойством Р |
| 3-й элемент класса S(S3) обладает (не обладает) свойством Р |
| …………………………………………………………………… |
| 30-й элемент класса S(S30) обладает (не обладает) свойством Р |
| S1, S2, S3,…,S30 – образуют весь класс S |
| Все S обладают (не обладают) свойством Р |
Например, результаты флюорографического обследования студенческой группы, факультета, жилого дома позволяют в случае добросовестной, т.е. полной индукции сделать заключение: «Никто из группы N… легочной патологии не имеет». Понятно, что рассуждения «по полной» индукции применимы лишь к конечным множествам, поэтому с обобщением такого вида в дальнейшем обращаются как с дедуктивным результатом. Например, теорема о сумме внутренних углов треугольника доказывается по методу полной индукции, путем последовательного рассмотрения трех видов треугольника (остроугольного, прямоугольного и тупоугольного). Аудиторская деятельность, составление свода юридических законов, каталогов моделей машин и др. используют возможность получения истинного заключения по интересующему вопросу при помощи полной индукции. Однако число таких случаев невелико. Чаще человек сталкивается с классом предметов, полный анализ элементов которых невозможен. В таком случае заключение делается по неполной индукции.
Неполная индукция 2. Неполная индукция – это такой вид индуктивного умозаключения, в ходе которого на основании принадлежности признака части элементов класса, делается заключение о принадлежности этого признака всему классу элементов.
| Схема неполной индукции |
| 1-й элемент класса S(S1) обладает (не обладает) свойством Р |
| 2-й элемент класса S(S2) обладает (не обладает) свойством Р |
| 3-й элемент класса S(S3) обладает (не обладает) свойством Р |
| …………………………………………………………………… |
| n-й элемент класса S(Sn) обладает (не обладает) свойством Р |
| S1, S2, S3,…,Sn – принадлежат классу S |
| Все S обладают (не обладают) свойством P |
Хотя неполная индукция дает лишь вероятностное заключение, однако это не снижает ее научно-познавательного значения. Ее выводы основываются на многократно повторяющейся повседневной и научной практике, устанавливающей причинно- следственную взаимосвязь явлений и процессов мира и позволяющей зафиксировать существенные, повторяющиеся свойства предметов. Физические, математические, технические, социальные и др. законы являются обобщением различных научных данных. «Жизненный опыт», выступающий условием простейшей человеческой деятельности, в то же время является итогом обыденных обобщений. Определение времени, необходимого, чтобы доехать до работы, анализ графика движения общественного транспорта, рабочего расписания магазинов, банков, народные приметы и многое другое невозможно без данной формы человеческой мысли.
Итак, истинность индуктивного вывода зависит от полноты и законченности опыта. Однако наряду с количественным параметром, большое значение имеет качественная оценка тех оснований, признаков, по которым отбирается эмпирический материал. Наименее вероятными, а значит наиболее ошибочными являются индукция через простое перечисление и индукция через отбор фактов. Наиболее вероятной формой неполной индукции является научная индукция, которая повышает степень достоверности выводов при помощи различных методов (наиболее разработанными являются пять методов) выявления сходных и различных признаков предметов.
