Линейная структура алгоритмов

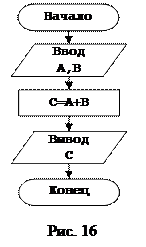Под понятием «действие», можно понимать любую операцию. Если это операция в области математики, то это может быть какая либо формула, если это операция в жизни человека, то это какое либо его действие. Например положить монету в телефон-автомат это действие или вычислит выражение c=a+b это тоже действие. Рассмотрим структуру алгоритма вычисления выражения C=A+B, приведенную на рисунке 16.

За основу берем общую структуру алгоритма, определяемся с исходными данными и результатами работы алгоритма. Для этого выражения исходные данные имеют символическое представление A и В, а результатом его работы будет сумма, имеющая символическое представление C. Следующим этапом необходимо определиться с процессом, который будет описывать алгоритм. В нашем случае, это вычисление суммы. Поставляем в общую структуру алгоритма наши выводы и получаем алгоритм вычисления суммы.

Рассмотренный пример содержит всего одно действие, по этому структура этого алгоритма получилась идентичной общей структуре алгоритмов.

Для более детального понимания шага, классифицируемого как действие, рассмотрим структуру алгоритма, состоящую не из одного, а из двух последовательных действий. Для примера возьмем следующую последовательность вычислений: C=A+B, E=C*D, графическое представление алгоритма которой 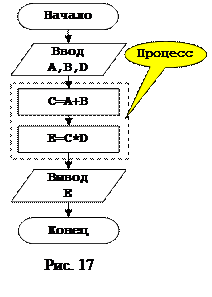представлено на рисунке 17. Проанализируем наши исходные данные. В первом выражении объекты(в данном случае числа) являющиеся исходными данными имеют символическое представление A и B, во втором выражении исходные данные имеют символическое представление C и D, однако объект, имеющий символическое представление C является результатом первого выражения, а соответственно не является исходными данными для алгоритма в целом. Следовательно исходными данными алгоритма в целом являются объекты, имеющие символическое представление A, B и D. Теперь разберемся с результатами работы алгоритма. В первом выражении результатом работы является объект, имеющий символическое представление C, а во втором объект, именуемый как E, однако объект C, является промежуточным результатом работы алгоритма. Отсюда делаем вывод, что результатом работы алгоритма является объект с символическим именем E. И последним этапом, идет анализ шагов, которые необходимо проделать для получения конечного результата. В нашей задачи предусмотрено два математических выражения, это C=A+B и E=C*D. Соответственно у нас должно быть два последовательных шага типа «действие» первый это C=A+B, а второй E=C*D. Обращаемся к общей структуре алгоритма, описывающий любой процесс. В блок «ввод данных» подставляем символические представления объектов, используемых в качестве исходных данных задачи это A, B и D, в качестве «процесса» вводим два последовательных действия это C=A+B и E=C*D. И наконец в блок «результаты» подставляем символическое представление результирующих объектов, в нашем случае это E. На этом процесс построения алгоритма решения задачи можно считать завершенным. Структуры алгоритмов, имеющие только последовательные действия имею общее название - линейные алгоритмы.

Структура развилки

В реальной жизни линейные или по другому безусловные алгоритмы встречаются крайне редко, поэтому в процесс алгоритмизации был введен второй вид шага, это шаг типа развилка. Шаг типа развилка предусматривает возможность внедрение в алгоритмы различные пути решения при различных исходных данных и ситуациях связанных с их обработкой. Другими словами шаг развилка это шаг проверки какого либо условия, если условие выполняется (то есть результат сравнения равен истине), то алгоритм идет по одному пути, если нет, то по другому. Рассмотрим этот вид алгоритмов на простом примере:

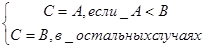
Как и в случае с линейным алгоритмом, сначала определимся с исходными данными. Из математического выражения видно, что исходные данных имеют символическое название A и B, и с результатами вычисления, исходя из того же выражения, это объект с именем C. Как и в предыдущем примере мы имеем два математически выражения, это C=A и C=B, однако исходное выражение содержит условие, то есть, в зависимости от исходных данным, в процессе выполнения алгоритма, должно быть выполнено только одно выражение. Если значение объекта A меньше значения объекта B, то выполнится первое выражение C=A, а если нет, то второе C=B. Получается, что в зависимости от исходных данных, алгоритм должен иметь два пути решения, либо выполняется первое выражение, либо второе.

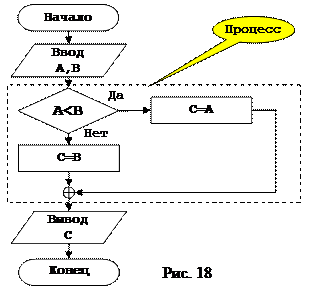Итак начинаем строить алгоритм решения поставленной задачи, рисунок 18. За основу как обычно берем общую структуру алгоритма, в блок «ввод данных» вводим символическое представление объектов, определенных как исходные данные, в нашем случае это A и B. Далее идет блок выполнения алгоритма. Поскольку поставленная задача может иметь два пути решения, вводим в блок процесса структуру развилки, и записываем в нее условие, которое является причиной различных путей решения, в нашем случае это A<B.Теперь у нас получилось два возможных пути решения, в случае выполнения условия, мы можем организовать один вычислительный процесс, а в случае его невыполнения другой, так и поступаем в случае выполнения условия организуем процесс, в котором будет выполняться шаг, выполняющий действие C=A, а в случае его невыполнения шаг на котором выполняется выражение C=B. После выполнения одного из возможных действий мы объединяем пути и организуем вывод результатов, для этого записываем в блок «результат» символическое название объекта, являющегося результирующим, в нашей задаче это объект C. На этом процесс построения алгоритма решения задачи можно считать завершенным.

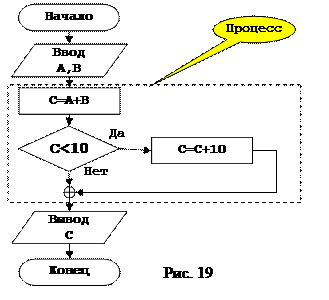Возможны варианты задач, в которых используется структура развилки, не имеющая шагов, в случае невыполнения условий, например: C=A+B, если C<10, то C=C+10, графическое представление алгоритма приведено на рисунке 19. Как и в предыдущих примерах, определяемся с исходными данными, здесь они имеют символические названия A и B, и с результатами работы алгоритма, это объект, имеющий символическое название C. Теперь рассмотрим непосредственно процесс выполнения алгоритма. У нас имеется два выражения, это C=A+B и C=C+10, однако, первое выражение выполняется всегда, а второе, только при определенных исходных данных, в нашем случае условием C<10. Следовательно, нам необходимо внедрить развилку, но с одним условием, что дополнительный шал алгоритма, появляется только при выполнение условия развилки. В случае его невыполнения, дополнительные шаги не предусматриваются. Итак, анализ задачи проведен, теперь обращаемся к общей структуре алгоритма. В блок «ввод данных», как и в предыдущих примерах вносим список символических представлений объектов, являющихся исходными данным, в блок процесса, первым шагом, вычисление выражения C=A+B, далее идет блок развилки C<10, в случае выполнения которого, вводим дополнительный шаг C=C+10, и последним нашим действием, будет запись в блок «результаты» символического представления результатов работы алгоритма, в нашем случае это объект C. Процесс разработки алгоритма завершен.

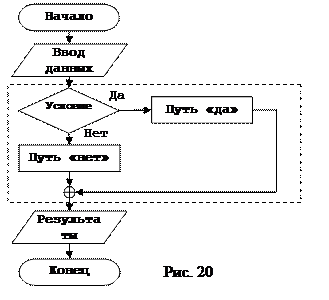
Общая структура алгоритма, использующего условное определение пути решения приведена на рисунке 20.

Структура цикла

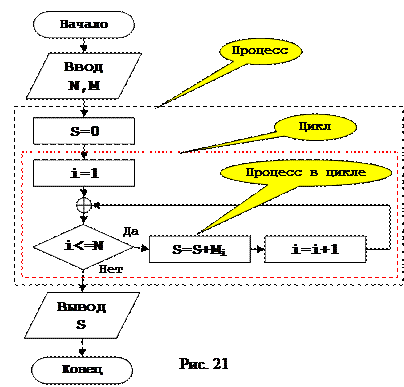
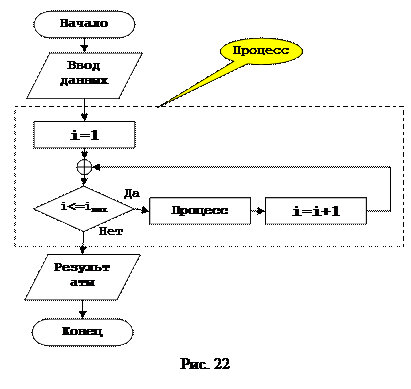
Очень часто в жизни встречаются повторяющиеся процессы, тое есть процессы, состоящие из определенных шагов, повторяющиеся до тех пор, пока не выполнится какое либо условие. Так например, повторять набор номера телефона, до тех пор, пока не будет установлено соединение. Различаются три основных вида циклических процессов. Первое, это циклический процесс со счетчиком.. Этот вид циклического процесса подразумевает повторение одних и тех же операций, определенное число раз. Например, телефонный номер состоит из 10 цифр, то есть для набора телефонного номера, нам необходимо ввести последовательность из 10 цифр. Получается, что для набора номера телефона, мы используем цикл со счетчиком, то есть по очереди набираем цифры с первой по десятую. Рассмотрим простой арифметический пример, вычисление суммы чисел последовательности M размерности N, рисунок 21. Как и в предыдущих примерах сначала определяемся с исходными данными. В данной задаче первым делом определяемся с исходными данными. В данном случае, это размерность N и сама последовательность M. И с результатами работы алгоритма. В данном случае это сумма S. Далее непосредственно с процессом, выполняемым внутри алгоритма. Для определения суммы всех элементов какой либо последовательности нам необходимо их всех сложить. Для складывания всех элементов любой последовательности M необходимо перебрать их всех. Для перебора всех элементов любой последовательности необходимо организовать цикл со счетчиком. Счетчик в данном случае необходим для определения текущего номера элемента, а так же определения конца последовательности, и при каждом повторении цикла прибавлять значение элемента к символическому объекту, определяющему сумму. Кроме того, поскольку мы определяем сумму элементов, необходимо начальное значение символического объекта S приравнять нулю, поскольку при определении суммы цифра «0» не меняет результата. Общая структура цикла со счетчиком приведена на рисунке 22.

Второй вид циклического процесса, это циклический процесс с предусловием. Этот вид циклического процесса применяется в ситуациях, когда процесс, повторяемый в цикле выполняется только в случае выполнения условия, причем перед началом цикла проверяется истинность этого условия. Цикл со счетчиком является частным случаем цикла с предусловием, однако в структуре цикла со счетчиком, за ранее известно сколько раз будет повторен процесс, а в общем случае цикла с предусловием нет. Цикл с предусловием, может не выполнится ни одного раза, если заранее заданы параметры невыполнимого условия, например, если телефон работает, то набирать номер пока не произойдет соединение. В этом примере видно, что для выполнения цикла должны выполниться условия «телефон работает» и «нет соединения», то есть если телефон не работает или соединение уже установлено цикл не выполниться ни одного раза. Рассмотрим алгоритм включающий в себя цикл с предусловием на примере. Найти сумму цифр от A_нач до A_кон с шагом dA, рисунок 23. Исходными данными для построения алгоритма решения задачи являются A_нач, A_кон и dA. Результатом работы алгоритма будет являться сумма, придадим ей символическое название S. Для решения этой задачи нам необходимо сложить все числа, которые входят в промежуток от A_нач до A_кон с шагом dA, то есть на первом шаге мы присвоим символическому объекту значение ноль S=0, на втором шаге мы прибавим к S=A_нач, далее S=S+dA,…, S=S+dA до тех пор, пока A_нач+n*A будет меньше или равно A_кон. Для того, чтобы не повторять одну и туже операцию некоторое количество раз и организуется цикл с предусловием, который будет выполнять этот процесс автоматически.

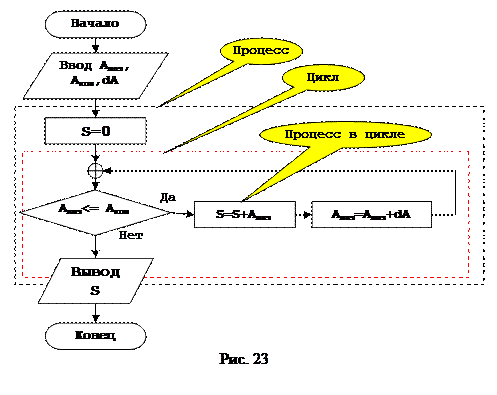
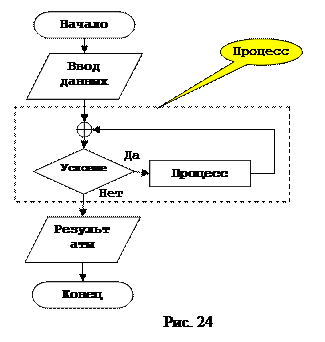
При выполнении циклического процесса, сначала проверяется условие, и если исходные данные заданы таким образом, что A_нач заранее больше A_кон, то при таких исходных данных процесс внутри цикла не выполнится ни разу. Общая структура алгоритма организации цикла с предусловием приведена на рисунке 24.

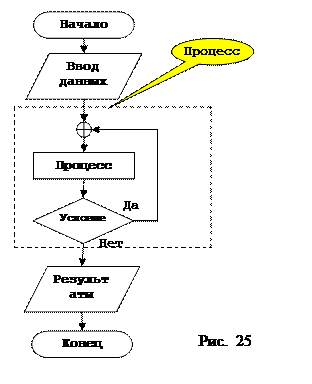
И последним вариантом циклического процесса является цикл с постусловием, единственным отличие данного вида цикла является то, что сначала выполняется какое либо действие, а затем проверяется, требуется повторить или нет. В примере с набором номера телефона, формулировка будет звучать так: набирать номер телефона и если нет соединения, то повторить. Общая структура алгоритма организации цикла с постусловием приведена на рисунке 25.

Приближенные вычисления.

При решении задач вычислительного характера, редко удается получить абсолютно точные результаты. Причинами этого являются участвующие в вычислениях операции деления. Если исходные числа были иррациональными, то точно представить их в виде конечных десятичных дробей невозможно, так как их запись содержит бесконечное число цифр. Поэтому, приходиться вместо исходных иррациональных чисел, оперировать рациональными числами, полученными из данных иррациональных чисел путем записи их в рациональном виде, путем записи их с конечным числом знаков, то есть округлении.

Возникают подобные ситуации, и в случае когда исходные числа были рациональными, а в результате операций над ними получились иррациональные, например при делении единицы на три получим 1/3=0,333…, в результате выполнения операций подобные числа так же округляются до конечного числа знаков.

Кроме того, одним из самых важных источников погрешности, является неточность самих исходных данных. Обычно исходные данные для большинства задач моделирования получают на основе физических экспериментов и опытов. Любой эксперимент связан с измерениями и наблюдениями, которые сами по себе не могут оказаться абсолютно точными в связи с возможностями измерительной аппаратуры. Даже при определении площади комнаты, когда необходимо знать только ее длину и ширину, как бы мы не старались, мы не сможем измерить абсолютно точно, даже сам измерительный прибор, заранее содержит какую то погрешность измерений. И естественно, при решении задач мы идеализируем их исходные данные, то есть вместо реальных задач решаем приближенную к реальности идеальную задачу, даже с измерением площади комнаты, углы не могут быть абсолютно прямыми, то есть комната заранее не является прямоугольником.

Пусть для величины, точное значение которой есть X, мы получили некоторое приближенное значение X^*. Абсолютная величина разности между точным значением X и его приближенное величиной X^*, называется абсолютной погрешностью. Приближенного числа X^*, и обозначается 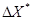, то есть, 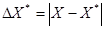. Как правило, точное значение X нам неизвестно, как неизвестна и абсолютная погрешность 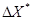. Но зато, можно определить число, которое эта погрешность заведомо не превосходит. Его обычно и принимают за абсолютное значение погрешности искомой величины. Так при взвешивании какого либо предмета на аптекарских весах, мы не можем определить точный вес предмета, однако гарантируем, что погрешность взвешивания не будет превышать 0,01 г. Эту величину и называют абсолютной погрешностью.

Абсолютная погрешность далеко не всегда точно характеризует погрешность вычислений. Так например, пусть погрешность взвешивания предмета равна 100 г, если взвешивался например автомобиль, то эта погрешность очень мала, а если взвешивался например телефон, то эта погрешность очень велика. Поэтому было введено еще одно важное, с точки зрения точности вычислений понятие – это относительная погрешность.

Относительной погрешностью приближенного значения X^* называют отношение абсолютной погрешности 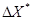к абсолютному значению величины.

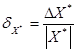
Для примера возьмем измерения длин радиоволн с абсолютной погрешностью равной одному метру. Если после измерений получим, что длина волны равна 1000 метров, то относительная погрешность равна 1/1000=0,001, а если длина волны равна 4 метрам, то относительная погрешность равна 1/4=0,25.

Для удобства анализа относительной погрешности очень часто ее представляют в виде процентов к значению измерений:

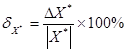
тогда, в результате решения задачи измерения длины волны, в случае если это километровый диапазон, то относительная погрешность составляет всего 0,1%, то есть очень мало, а если метровый, то 25%, то есть очень много.

Как говорилось ранее, очень часто в процессе вычислений приходиться иметь дело с бесконечными дробями. Такие числа приходиться округлять. Обычно округление производят по следующему правилу (иногда бывает необходимость использования и других правил). Пусть какое то число имеет в своей записи более чем k цифровых знаков и мы хотим округлить его, оставив ровно k знаков. Тогда, если (k+1)-я цифра числа меньше чем 5, то все ее цифры, начиная с (k+1)-ой просто отбрасываются, а если (k+1)-я цифра больше чем 5, то все цифры, начиная с (k+1)-ой тоже отбрасываются, при этом k-я цифра увеличивается на единицу. Если (k+1)-я цифра есть 5, а за ней найдется хоть одна отличная от нуля цифра, то поступают, как в случае, если (k+1)-я цифра больше пяти, если за ней нет цифр отличных от нуля, тогда отбрасывают «хвост», начиная с (k+1)-ой цифры, и если k-я цифра четная, то оставляют ее без изменений, если нечетная, увеличивают на единицу. Например, оставив три знака после запятой в числе 5,6785 поучим 5,678, а если оставим три знака после запятой в числе 4,5675, то получим 4,568.

Принято считать, что в приближенном значении величины все цифры верные, если его абсолютная погрешность не превосходит единицы последнего разряда. При выполнении этого условия можно по записи приближенного значения определить его абсолютную погрешность. И наоборот, по абсолютной погрешности числа, можно определить число верных знаков в его записи. Например, если известно, что все цифры записи числа X=15 верны, то его абсолютная погрешность 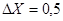, а если известно, что все цифры записи числа X=3,14 верны, то его абсолютная погрешность 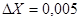. Аналогично наоборот, если задано число X=1,2345 и абсолютная погрешность при этом 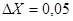, то можно говорить о том, что верны только цифры 1 и 2, то есть можно считать верным только число X=1,2 и в окончательном результате остальные цифры должны отбрасываться.

В процессе алгоритмизации, то есть разработки алгоритмов решения различных задач следует обратить должное внимание на качество вычислительных и измерительных операций и анализу погрешности результатов.