Тестовые примеры построения СФЦ и применения технологии АСМ

Возможно, что следующие примеры могут показаться излишне простыми. Но главная цель их рассмотрения заключается в начальном освоении заинтересованным читателем новых возможностей постановки и решения, на единой теоретической и методической базе ОЛВМ, СФЦ, технологии и ПК АСМ, различных задач моделирования и количественной оценки свойств надежности (безотказности), стойкости, живучести, комплексной устойчивости, эффективности, технического риска и ожидаемого ущерба функционирования систем.

Исходная функциональная схема (блок-схема) работоспособности рассматриваемой двухэлементной дублированной системы приведена на рис.3.

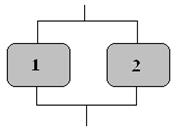
Рис.3. Функциональная схема работоспособности дублированной системы из двух элементов

По каждому из указанных выше свойств устойчивости, эффективности и риска функционирования данной двухэлементной системы, далее приводятся результаты построения СФЦ и автоматизированного моделирования и расчетов показателей, полученные с помощью комплексов АРБИТР [1] и ПК АСМ 2001 [8, 9]. Эти результаты несложно проверить путем ручного аналитического решения соответствующих задач.

Модель надежности (безотказности) системы. Под надежностью(безотказностью ) понимается способность системы сохранять (или не сохранять) работоспособность при случайных реализациях элементарных событий возникновения отказов и восстановлений ее элементов в нормальных (заданных) условиях эксплуатации (определение не противоречит ГОСТ 27.002-89).

На первом этапе технологии АСМ строится СФЦ надежности (безотказности) рассматриваемой двухэлементной системы. Применяя событийно-логический подход к анализу функциональной схемы системы (см. рис.3) и графический аппарат СФЦ (см. рис.1), выделяем два случайных события 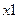, 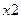безотказной работы (или готовности) элементов. В разрабатываемой СФЦ на рис.6 они представлены двумя функциональными вершинами с номерами 1 и 2 соответственно.

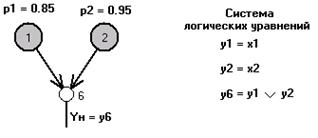
Рис.4. СФЦ надежности системы

Положим, что параметры надежности (безотказности, готовности) элементов составляют 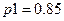и . И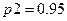сходящие из функциональных вершин дуги 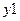, 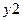представляют на графе СФЦ логические условия реализации каждым элементом своих функций в системе. Заходящие в фиктивную вершину 6 дизъюнктивные дуги 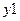, 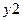(операция "ИЛИ", см. рис.1 и рис.2) представляют условие 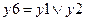, которое является логическим критерием 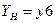надежности (безотказности, готовности) рассматриваемой системы в целом.

На рис.4 справа приведены логические уравнения для выходов всех трех вершин построенной СФЦ, которые всегда могут быть записаны на основе базовых логических соотношений, приведенных на рис.2. Эта система уравнений является точным аналитическим (логическим) аналогом разработанной СФЦ надежности системы. В программных комплексах технологии АСМ системы логических уравнений формируются автоматически (в процессе ввода графа СФЦ) и далее используются для автоматического логического моделирования.

На втором этапе ОЛВМ, на основе разработанной СФЦ и заданного логического критерия, программный комплекс АРБИТР автоматически решает соответствующую систему логических уравнений (см. рис.4) и определяет логическую функцию надежности системы

.

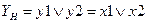Далее, на третьем этапе ОЛВМ, ПК АРБИТР автоматически преобразует полученную логическую функцию в правильный многочлен расчетной вероятностной функции (для гипотезы о независимости событий 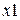и )

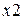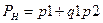, где .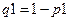

На завершающем четвертом этапе ОЛВМ комплекс АРБИТР выполняет (используя многочлен вероятностной функции) точный расчет искомой вероятностной характеристики надежности системы – вероятности безотказной работы

.

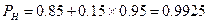Модель стойкости (условной живучести) системы. Под структурной стойкостью (условной живучестью) [7] будем понимается способ­ность системы сохранять (или не сохранять) работоспособность при случайных поражениях (или непоражениях) ее элементов вследствие воздействия достоверно возникающих поражающих факторов определенного вида (ударов, взрывов, пожаров и т.п.). Здесь условность живучести определяется достоверностью возникновения поражающих факторов, а надежность элементов считается абсолютной.

На первом этапе, для построения СФЦ стойкости рассматриваемой системы, вводятся два новых элементарных случайных событи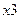й и 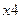независимого поражения элементов 1 и 2 системы достоверным поражающим фактором (см. рис.5).

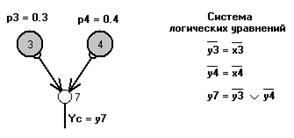
Рис.5. СФЦ стойкости системы

В СФЦ стойкости случайные события поражения элементов 1 и 2 представляются соответствующими функциональными вершинами 3 и 4. Тогда условиями непоражения (стойкости) элементов 1 и 2 (сохранения их работоспособности) становятся инверсные выходные дуги 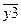, 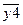из указанных вершин. На выходе фиктивной вершины 7 представлено условие 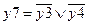, которое является логическим критерием 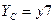стойкости исследуемой системы в целом. Положим, что поражения элементов 1 и 2 воздействием достоверно возникающего поражающего фактора происходят независимо с вероятностями 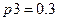, 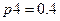соответственно. Надежность элементов исследуемой системы считается абсолютной.

Результаты следующих этапов автоматического построения комплексом АРБИТР логической и вероятностной математических моделей и расчета вероятности непоражения системы достоверно возникающим поражающим фактором (ее стойкости, условной живучести) составляют:

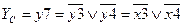- логическая функция стойкости системы;

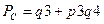- многочлен расчетной вероятностной функции стойкости системы

(здесь 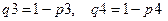- параметры стойкости элементов);

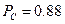- вероятностный показатель стойкости исследуемой системы.

В последние годы все большее внимание начинает уделяться вопросам детерминированного анализа условной живучести (стойкости) сложных систем. Программные средства детерминированного анализа живучести должны точно и однозначно показывать, какие из всего множества функций системы прекратят работать и какие функции сохраняться после достоверного поражения различных заданных групп элементов системы. В настоящее время АРБИТР позволяет решать задачи детерминированного анализа стойкости (условной живучести) систем большой размерности и высокой структурной сложности с корректным учетом неограниченного количества циклических (мостиковых) связей, размноженных вершин и групп несовместных событий.

Модель живучести системы. Под структурной живучестью (полной, безусловной живучестью) [7] будем понимать способ­ность системы сохранять (или не сохранять) работоспособность при случайных поражениях (непоражениях) ее элементов вследствие случайного (недостоверного) возникновения поражающих факторов (ударов, взрывов, пожаров и т.п.). При этом надежность элементов системы считается абсолютной.

Для учета в структурной модели живучести рассматриваемой двухэлементной системы случайности возникновения поражающего фактора, в разрабатываемую СФЦ вводится еще одно новое событие 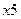- возникновение поражающего фактора. Свершение этого события является обязательным условием последующего воздействия и возможного (случайного) поражения (или непоражения) элементов 1 и/или 2 системы. Если поражающий фактор не возникает, то элементы 1 и 2 непоражаются достоверно.

Путем дополнения ранее разработанной СФЦ стойкости (см. рис. 5) функциональной вершиной 5 (возникновение поражающего фактора) и указанием на графе дугами 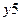условий обеспечения событий 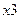, 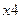(поражения элементов 1 и 2), строится СФЦ полной живучести рассматриваемой системы (см. рис.6).

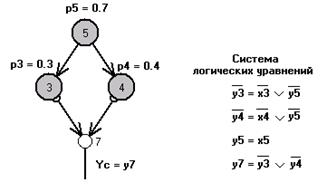
Рис.6. СФЦ живучести системы

Здесь на выходе фиктивной вершины 7 (как и в предыдущем примере) представлено условие 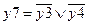сохранения работоспособности хотя бы одним элементом, которое теперь является критерием 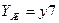живучести системы при случайном возникновении и воздействии поражающего фактора. Положим, что возникновение поражающего фактора происходит с вероятностью 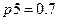. Вероятности 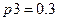, 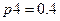являются ранее заданными параметрами нестойкости (поражения) элементов 1 и 2 при возникновении поражающего фактора.

Результаты следующих этапов моделирования и расчета живучести системы, автоматически полученные с помощью ПК АРБИТР, составляют:

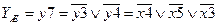- логическая функция стойкости системы;

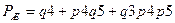- многочлен вероятностной функции живучести

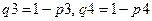( - параметры стойкости элементов);

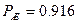- вероятностный показатель живучести исследуемой системы.

Следует отметить, что разработанная СФЦ полной живучести рассматриваемой двухэлементной системы (см. рис.6), является немонотонной по построению. Это означает, в частности, что ни с помощью типовых блок-схем, ни с помощью типовых деревьев отказов аналогичная структурная модель полной живучести не может быть построена. Вместе с тем, полученные логическая и вероятностная функции живучести еще остаются монотонными, в рамках принятых содержательных определений используемых элементарных событий.

Модель устойчивости системы. Под структурной устойчивостью будем понимать комплексную характеристику способ­ности системы сохранять (или не сохранять) работоспособность, определяемую различными совместными комбинациями свойств ее структурной надежности, стойкости и живучести.

Объединяя ранее разработанные СФЦ (см. рис.4, рис.5 и рис. 8), строим структурную модель комплексной устойчивости рассматриваемой двухэлементной системы в целом (см. рис.7).

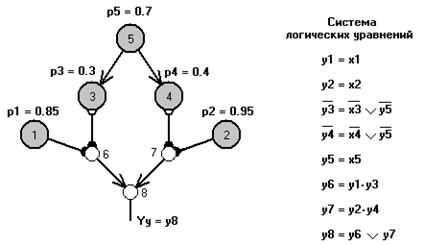
Рис.7. СФЦ устойчивости системы

Здесь на выходе фиктивной вершины 6 представлено условие 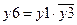сохранения работоспособности (и неотказа, и непоражения) элемента 1. На выходе фиктивной вершины 7 представлено аналогичное условие сохранения работоспособности для элемента 2 исследуемой системы. На выходе фиктивной вершины 8 представлено условие 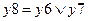сохранения работоспособности хотя бы одним элементом, которое является логическим критерием 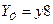комплексной устойчивости рассматриваемой системы в целом. Остальные фрагменты данной СФЦ были рассмотрены в предыдущих примерах. Все заданные вероятностные параметры элементов остались прежними.

Результаты последующих этапов автоматизированного моделирования и расчета устойчивости системы, полученные с помощью ПК АРБИТР, составляют:

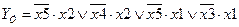- логическая функция устойчивости системы;

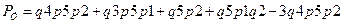- многочлен расчетной вероятностной

функции;

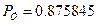- вероятностный показатель устойчивости исследуемой системы.

Следует отметить, что разработанная СФЦ комплексной устойчивости (см. рис.6) рассматриваемой двухэлементной системы (см. рис.3), а также ее логическая и вероятностная функции является немонотонными. Это означает, в частности, что с помощью типовых блок-схем или деревьев отказов аналогичная структурная модель устойчивости не может быть построена. Конъюнкции логической функции уже не представляют ни классические КПУФ ни классические МСО системы, а образуют их немонотонные комбинации. Немонотонность полученного многочлена вероятностной функции проявляется, в частности, в том, что увеличение вероятностей одних элементарных событий (например 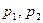) приводит к увеличению значения 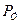, а других событий (например, 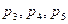) приводит к уменьшению значения этого показателя.

Модель реальной эффективности системы. В ГОСТ 27.003-90 и ГОСТ 27.301 [18] введено понятие "изделие вида II", которое может находиться в некотором числе 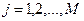частично неработоспособных состояний (состояний частичного отказа и/или поражения) 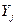. Каждое 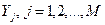характеризуется соответствующим значением 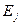условной (идеальной) эффективности функционирования системы в этих состояниях. Будем такие системы называть качественно сложными. Тогда под реальной эффективностью 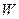качественно сложной системы понимается математическое ожидание значения показателя эффективности ее функционирования при случайном нахождении (по причинам неабсолютной устойчивости) в состояниях 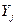полной и частичной работоспособности.

Для ранее рассмотренного примера устойчивости двухэлементной системы (см. рис.7) положим, что общее условие ее работоспособности 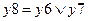характеризуется тремя качественно различными несовместными областями состояний:

1. 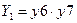состояния полной работоспособности, эффективность системы ;

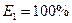2. 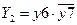состояния частичной работоспособности, эффективность системы ;

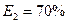3. 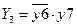состояния частичной работоспособности, эффективность системы .

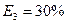Соответствующая данным условиям СФЦ реальной эффективности двухэлементной системы (см. рис.3) приведена на рис.8.

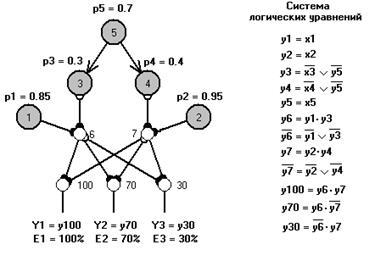
Рис.8. СФЦ реальной эффективности системы

Для удобства представления условий реализации состояний 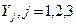разных уровней условной эффективности системы, в разрабатываемую СФЦ реальной эффективности вводятся три фиктивные вершины с номерами 100, 70 и 30 соответственно (см. рис.8).

На выходах фиктивных вершин 100, 70 и 30 представляются условия (критерии) функционирования системы с различными уровнями условной эффективности в 100%, 70% и 30% соответственно. Автоматизированное моделирование и расчет в программных комплексах АСМ реальной эффективности данной системы осуществляются на основе составного критерия

.

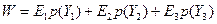Результаты следующих этапов автоматизированного моделирования и расчета реальной эффективности двухэлементной системы (см. рис.3), полученные с помощью ПК АРБИТР, составляют:

;

;

;

;

;

;

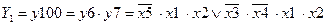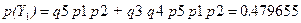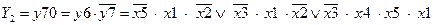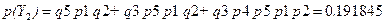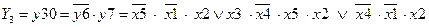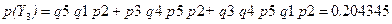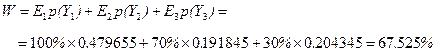
Полученные результаты позволяют дополнительно определить вероятность нахождения системы в состоянии работоспособности (устойчивости)

,

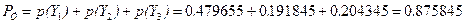которая совпадает с полученной в предыдущем примере оценкой комплексной устойчивости рассматриваемой системы.

Следует отметить, что разработанная СФЦ (см. рис.8), логическая и вероятностные функции реальной эффективности рассматриваемой системы являются немонотонными.

Модель технического риска по надежности. Технический риск, согласно РД-03-418-01, является одним из показателей риска аварии на опасном производственном объекте и оценивается вероятностью отказов технических устройств, приводящих к возникновению аварии с последствиями (ущерб, потери, разрушения и т.п.) определенного уровня (класса) за определенный период времени функционирования системы [19].

Для иллюстрации применения технологии АСМ в расчетах технического риска сначала воспользуемся ранее рассмотренной моделью надежности двухэлементной системы (см. СФЦ на рис.4). Положим, что различные комбинации 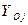отказов элементов приводят к авариям системы с различными уровнями 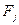последствий, которые оцениваются в условных единицах ущерба (потерь):

- , ;

- , ;

- , .

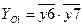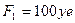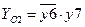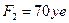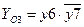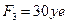Для построения СФЦ технического риска (см. рис.9) ранее рассмотренная СФЦ надежности (см. рис.4) дополняется тремя фиктивными вершинами с номерами 100, 70 и 30 соответственно (см. рис.9).

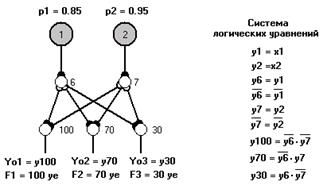
Рис.9. СФЦ технического риска по надежности

С помощью заходящих в вершины 100, 70 и 30 дуг логических связей функционального подчинения, от вершин 6 и 7 представляются логические условия возникновения различных аварий, а на их выходах задаются логические критерии аварии системы с различными уровнями последствий:

- ;

- ;

- .

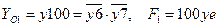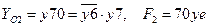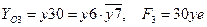Автоматизированное моделирование и расчет, с помощью ПК АРБИТР, технического риска 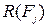по надежности рассматриваемой системы осуществляются отдельно по каждому из указанных критериев:

;

;

.

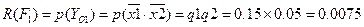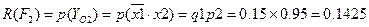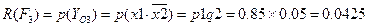Следует отметить, что СФЦ для анализа технического риска по надежности (см. рис.9) в целом, логические и вероятностные модели для аварий с последствиями 70 и 30 уе. являются немонотонными, несмотря на то, что исходная общая модель надежности системы была и остается монотонной по построению.

Модель ожидаемого ущерба по надежности. Ожидаемый ущерб, согласно РД-03-418-01, есть математическое ожидание величины ущерба от возможной аварии за определенное время [19].

Поэтому, для моделирования и расчета ожидаемого ущерба 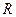по надежности может использоваться та же СФЦ технического риска, изображенная на рис.9. Только теперь для расчета ожидаемого ущерба с помощью ПК АСРБИТР необходимо задать соответствующий составной критерий

.

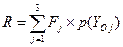На основе этого критерия ПК АСМ автоматически формирует модели и вычисляет значение ожидаемого ущерба по надежности системы

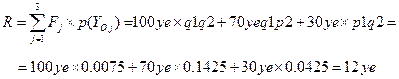
Модель ожидаемого ущерба по устойчивости. ОЛВМ, технология и ПК АСМ позволяют расширить области анализа технического риска и ожидаемого ущерба на стойкость, живучесть и комплексную устойчивость систем исследуемых опасных производственных объектов и процессов. Для этого в рассматриваемом примере достаточно выполнить преобразования постановок задач в рассмотренных ранее моделях (см. рис.5, рис.6 и рис.7) аналогичные тем, которые были сделаны в двух предыдущих примерах.

Для иллюстрации этого выполним с помощью ПК АСМ автоматизированное построение моделей и расчет показателей технического риска и ожидаемого ущерба с учетом комплексной устойчивости рассматриваемой двухэлементной системы. Преобразованная для анализа рисков СФЦ структурной модели устойчивости (см. рис.7) изображена на рис.10.

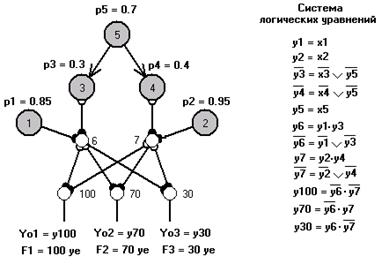
Рис.10. СФЦ риска по устойчивости

Здесь на выходах фиктивных вершин 100, 70 и 30 представлены условия (критерии) аварии системы с различными уровнями последствий в 100уе 70уе и 30уе соответственно (аналогично двум предыдущим примерам). Однако, в СФЦ на рис.10 учтены и надежность, и стойкость элементов к поражающему фактору, и вероятность его возникновения. Это позволяет с помощью ПК АСМ автоматически построить логические и вероятностные модели и рассчитать технический риск каждого вида возможной аварии и общий ожидаемый ущерб, вызванные и отказами элементов и поражающими воздействиями. Результаты моделирования и расчетов показателей технического риска и ожидаемого ущерба системы по устойчивости, полученные с помощью ПК АСМ, следующие.

1. Технические риски по устойчивости:

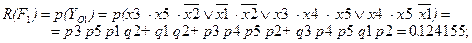
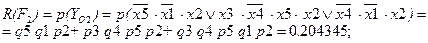
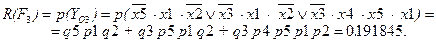
2. Ожидаемый ущерб по устойчивости

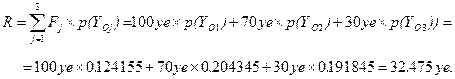
Рассмотренные тестовые примеры иллюстрируют основные положения практического применения общей технологии АСМ и подтверждают принципиальную возможность моделирования и расчета показателей всех наиболее важных отдельных и комплексных свойств устойчивости, эффективности и риска функционирования систем. При этом все основные модели и показатели определены в соответствии с действующими руководящими документами и государственными стандартами в области надежности, безопасности и риска сложных систем ОПО и ОИАЭ [19, 20, 22, 23 и др.].

Правильность решения всех рассмотренных выше тестовых примеров не сложно проверить вручную, что и предлагается сделать заинтересованному читателю. Теперь эту технологию можно применить для постановки и решения более сложных и высокоразмерных задач моделирования и расчета устойчивости, эффективности и риска функционирования реальных системных объектов с помощью ПК АРБИТР.

Список литературы

1. АРБИТР, "Программный комплекс автоматизированного структурно-логического моделирования и расчета надежности и безопасности систем (ПК АСМ СЗМА), базовая версия 1.0". Автор Можаев А.С. Правообладатель ОАО "СПИК СЗМА". // Свидетельство об официальной регистрации № 2003611101. М.: РОСПАТЕНТ РФ, 2003. // Аттестационный паспорт №222 от 21 февраля 2007 г., выдан Советом по аттестации программных средств НТЦ ЯРБ Федеральной службы по экологическому, технологическому и атомному надзору (Ростехнадзор) РФ.

2. Можаев А.С., Киселев А.В., Струков А.В., Скворцов М.С. Отчет о верификации программного средства "Программный комплекс автоматизированного структурно-логического моделирования и расчета надежности и безопасности систем" (АРБИТР, ПК АСМ СЗМА, базовая версия 1.0). Заключительная редакция с приложениями. СПб.: ОАО "СПИК СЗМА", 2007. – 1031 с.

3. Можаев А.С. Общий логико-вероятностный метод анализа на­дежности сложных систем. Уч. пос. Л.: ВМА, 1988. - 68с.

4. Можаев А.С. Общий логико-вероятностный метод автоматизированного структурно-логического моделирования надежности, безопасности и риска сложных систем. Многотомное издание "Безопасность России". Анализ риска и проблем безопасности. В четырех частях. Часть I. Основы анализа и регулирования безопасности. М.: МГФ "Знание", 2006, 640 с. (с. 153-197).

5. Черкесов Г. Н., Можаев А.С. Логико-вероятностные методы рас­чета надежности структурно-сложных систем. // В кн. Надежность и качество изделий. М.: Знание, 1991, с. 34-65.

6. Можаев А.С. Общий логико-вероятностный метод и технология моделирования безопасности сложных систем. Многотомное издание "Безопасность России". Анализ риска и проблем безопасности. В четырех частях. Часть III. Прикладные вопросы анализа рисков критически важных объектов, 2007, 816 с. (с. 243-293).

7. Можаев А.С. Автоматизированное структурно-логическое моделирование систем. Учебник. СПб: ВМА им Кузнецова Н.Г, 2006. - 590 с.

8. Можаев А.С., Гладкова И.А. Программный комплекс автоматизированного структурно-логического моделирования сложных систем 2001 (ПК АСМ 2001). // Свидетельство об официальной регистрации № 2003611099. М.: РОСПАТЕНТ РФ, 2003.

9. Можаев А.С. Программный комплекс автоматизированного структурно-логического моделирования сложных систем (ПК АСМ 2001). // Труды Международной Научной Школы 'Моделирование и анализ безопасности, риска и качества в сложных системах' (МА БРК – 2001). СПб.: Издательство ООО 'НПО 'Омега', 2001, с.56-61.

10. Можаев А.С., Гладкова И.А. Библиотека программных модулей автоматического построения монотонных и немонотонных логических функций работоспособности систем и многочленов вероятностных функций (ЛОГ&ВФ). // Свидетельство об официальной регистрации № 2003611100. М.: РОСПАТЕНТ РФ, 2003.

11. Можаев А.С. Универсальный графоаналитический метод, алгоритм и программный модуль построения монотонных и немонотонных логических функций работоспособности систем. // Труды Международной научной школы: "Моделирование и анализ безопасности, риска в сложных системах" (МА БР – 2003). СПб.: СПбГУАП, 2003, c.101-110.

12. Risk Spectrum PSA Professional 1.20 / Theory Manual. RELCON AB, 1998. - 57p.

13. Викторова В.С., Кунтшер Х., Петрухин Б.П., Степанянц А.С. Relex - программа анализа надежности, безопасности, рисков. // "Надежность" №4(7), 2003, с. 42-64.

14. Бахметьев А.М., Былов И.А., Милакова Ю.В. Отчет о научно-исследовательской работе "Верификация и обоснование программы CRISS 4.0 для моделирования и анализа систем безопасности ядерной установки при выполнении вероятностного анализа безопасности". Часть 1 (Заключительная редакция). Нижний Новгород: ФГУП ОКБМ им. И.И.Африкантова, 2005. - 88 с.

15. Рябинин И.А., Черкесов Г.Н. Логико-вероятностные методы исследования надежности структурно-сложных систем. М.: Радио и связь, 1981.

16. Рябинин И.А. Три кита ВМФ: надежность, живучесть, безопасность. Новочеркасск: ООО НПО "Темп", 2006, - 116 с.

17. Рябинин И.А. Надежность и безопасность структурно-сложных систем. СПб.: Издательство Санкт-Петербургского университета, 2007 г., 278 с.

18. ФГУП СПбАЭП, ОАО "СПИК СЗМА", (Санкт-Петербург), ИПУ РАН им. В.А.Трапезникова (г.Москва). НИР "Сравнительный анализ технологий деревьев отказов и автоматизированного структурно-логического моделирования, используемых для выполнения работ по вероятностному анализу безопасности АЭС и АСУТП на стадии проектирования" (шифр "Технология 2004"), 2005. - 282 с.

19. ГОСТ 27.301-95. Надежность в технике. Расчет надежности. Основные положения. М.: ИПК Издательство стандартов, 1996, 15 с.

20. РД 03-418-01. Методические указания по проведению анализа риска опасных производственных объектов. // Нормативные документы межотраслевого применения по вопросам промышленной безопасности и охраны недр. Серия 3. Выпуск 10. М.: Госгортехнадзор России, НТЦ "Промышленная безопасность", 2001, 60 с.

21. Ш.В.Камынов, М.И.Рылов, А.С.Можаев, А.А.Нозик. Методика применения программного комплекса АСМ СЗМА для расчета показателей безотказности и безаварийности стенда физических измерений. // Журнал "Управление риском", №1. М.: Издательство "АНКИЛ", 2007, с. 63-72.

22. НП-038-02. Общие положения обеспечения безопасности радиационных источников. // Федеральные нормы и правила в области использования атомной энергии. М.: Госатомнадзор России, 2002, - 37 с.

23. НП-024-200. Требования к обоснованию возможности продления назначенного срока эксплуатации объектов использования атомной энергии. // Федеральные нормы и правила в области использования атомной энергии. М.: Госатомнадзор России, 2000, - 15 с.

24. Поленин В.И., Рябинин И.А., Свирин С.К. Гладкова И.А. Применение общего логико-вероятностного метода для анализа технических, военных организационно-функциональных систем и вооруженного противоборства. Монография, под ред. проф. Можаева А.С. – СПб.: НИКА, 2011. – 410 с.