Решения и критерии школьного этапа

Класс Школьный этап всероссийской олимпиады школьников по математике

Решения и критерии школьного этапа

За каждое задание можно получить 7 баллов.

Основные принципы оценивания приведены в таблице.

Баллы	Правильность (ошибочность) решения
	Полное верное решение.
5-6	Решение содержит незначительные ошибки, пробелы в обоснованиях, но в целом верно и может стать полностью правильным после небольших исправлений или дополнений.
	Верно рассмотрен один из двух (более сложный) существенных случаев.
2-3	Доказаны вспомогательные утверждения, помогающие в решении задачи.
	Рассмотрены отдельные важные случаи при отсутствии решения (или при ошибочном решении).
	Решение неверное, продвижения отсутствуют.
	Решение отсутствует.

Помимо этого, в методических рекомендациях по проведению Олимпиады следует проинформировать жюри школьного этапа о том, что:

а) любое правильное решение оценивается в 7 баллов. Недопустимо снятие баллов за то, что решение слишком длинное, или за то, что решение школьника отличается от приведённого в методических разработках или от других решений, известных жюри; при проверке работы важно вникнуть в логику рассуждений участника, оценивается степень её правильности и полноты;

б) олимпиадная работа не является контрольной работой участника, поэтому любые исправления в работе, в том числе зачеркивание ранее написанного текста, не являются основанием для снятия баллов; недопустимо снятие баллов в работе за неаккуратность записи решений при её выполнении;

в) баллы не выставляются «за старание Участника», в том числе за запись в работе большого по объёму текста, но не содержащего продвижений в решении задачи;

г) победителями олимпиады в одной параллели могут стать несколько участников, набравшие наибольшее количество баллов, поэтому не следует в обязательном порядке «разводить по местам» лучших участников олимпиады (это решает районное олимпиадное Жюри, разрабатывающее положение о победителях и призёрах школьного этапа олимпиады).

Ответы к задачам олимпиады:

Задача № 1: Дедка вдвое сильнее Бабки, Бабка втрое сильнее Внучки, Внучка вчетверо сильнее Жучки, Жучка впятеро сильнее Кошки, Кошка вшестеро сильнее Мышки. Дедка, Бабка, Внучка, Жучка и Кошка вместе с Мышкой могут вытащить Репку, а без Мышки – не могут. Сколько надо позвать Мышек, чтобы они смогли сами вытащить Репку?

Решение:

Кошка заменяет 6 Мышек. Жучка заменяет 5х6 Мышек. Внучка заменяет 4х5х6 Мышек. Бабка заменяет 3х4х5х6 Мышек. Дедка заменяет 2х3х4х5х6 Мышек. Итого потребуется:

(2х3х4х5х6) + (3х4х5х6) + (4х5х6) + (5х6) + 6 +1 = 1237 Мышек.

Ответ: 1237 Мышек

Баллы	Правильность (ошибочность) решения
	Полное верное решение.
	Решение содержит незначительные вычислительные ошибки.
	Решение содержит пробелы в обоснованиях.
	Верно подсчитано, сколько Мышек заменяет Дедка.
	Верно подсчитано, сколько Мышек заменяет Бабка.
	Верно подсчитано, сколько Мышек заменяет Жучка и Внучка.
	Верно подсчитано, сколько Мышек заменяет Жучка.
	Решение неверное, продвижения отсутствуют.
	Решение отсутствует.

Задача № 2. У Джузеппе есть лист фанеры, размером 22 х 15. Джузеппе хочет из него вырезать как можно больше прямоугольных заготовок размером 3 х 5. Как это сделать и сколько их получится?

Решение:

Прежде всего заметим, что Джузеппе не сможет получить заготовок больше, чем (22х15):(3х5) = 22 штуки. Теперь приступим к разрезанию.

Разрежем наш лист на три части поперёк (режем сторону длиной 22): 5х15, 5х15 и 12х15. Теперь третий кусок разрежем вдоль стороны длиной 12 на четыре равных куска по 3х15. Всего получится 6 кусков – два по 5х15 и четыре по 3х15. Из первых двух кусков мы получим 10 заготовок по 5х3, а из оставшихся четырёх – 12 заготовок по 3х5. Итого получится 22 куска.

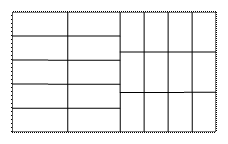
Ответ: 22 куска

Баллы	Правильность (ошибочность) решения
	Полное верное решение, в том числе предъявлена верная картинка.
5-6	Решение содержит незначительные ошибки, пробелы в обоснованиях, но в целом верно и может стать полностью правильным после небольших исправлений или дополнений.
	Правильно сказано, как можно разрезать один из кусков.
2-3	Найдено количество кусков.
	Рассмотрены отдельные важные случаи при отсутствии решения (или при ошибочном решении).
	Решение неверное, продвижения отсутствуют.
	Решение отсутствует.

Задача № 3. Когда Гулливер попал в Лилипутию, он обнаружил, что там все вещи ровно в 12 раз короче, чем на его родине. Сможете ли вы сказать, сколько лилипутских спичечных коробков поместится в спичечный коробок Гулливера?

Решение:

В гулливерском спичечном коробке должно помещаться 12 лилипутских коробков в ширину, 12 – в длину и 12 – в высоту. Всего 12х12х12 = 1728 коробков.

Ответ: 1728 коробков

Баллы	Правильность (ошибочность) решения
	Полное верное решение.
	Решение содержит вычислительные ошибки.
	Решение содержит погрешности в рассуждениях.
2-4	Доказаны вспомогательные утверждения, помогающие в решении задачи. Дана формула объёма коробка.
	Подсчитано количество коробков в одном слое.
	Решение неверное, продвижения отсутствуют.
	Решение отсутствует.

Задача № 4. Начнем считать пальцы на правой руке: первый – мизинец, второй – безымянный, третий – средний, четвёртый – указательный, пятый – большой, шестой – снова указательный, седьмой – снова средний, восьмой – безымянный, девятый – мизинец, десятый – безымянный и т.д. Какой палец будет по счёту 1992-м?

Решение:

Первый палец – мизинец, а затем всё время повторяется группа из восьми пальцев: безымянный, средний, указательный, большой, указательный, средний, безымянный, мизинец. Когда мы станем перечислять пальцы, первым будет мизинец, затем 248 раз повторяется группа из восьми пальцев, а потом – последние семь. Седьмой палец в нашем списке – безымянный.

Ответ: безымянный

Баллы	Правильность (ошибочность) решения
	Полное верное решение.
5-6	Решение содержит незначительные ошибки, пробелы в обоснованиях, но в целом верно и может стать полностью правильным после небольших исправлений или дополнений.
	Указано, что потом – последние семь.
2-3	Указано, что повторяется группа из восьми пальцев.
	Рассмотрены отдельные важные случаи при отсутствии решения (или при ошибочном решении).
	Решение неверное, продвижения отсутствуют.
	Решение отсутствует.

Задача № 5. Дорога от дома до школы занимает у Пети 20 минут. Однажды по дороге в школу он вспомнил, что забыл дома ручку. Если теперь он продолжит свой путь с той же скоростью, то придёт в школу за 3 минуты до звонка, а если вернётся домой за ручкой, то, идя с той же скоростью, опоздает к началу урока на 7 минут. Какую часть пути он прошёл до того, как вспомнил о ручке?

Решение:

Если Петя вернётся домой за ручкой, то на весь путь он потратит на 3 + 7 = 10 минут больше, чем потратил бы, если бы не возвращался. Это значит, что путь от того места, где он вспомнил про ручку, до дома и обратно занимает 10 минут. Следовательно, Петя вспомнил про ручку в 5 минутах ходьбы от дома, т.е. он прошёл ¼ пути.

Ответ: ¼ пути

Баллы	Правильность (ошибочность) решения
	Полное верное решение.
5-6	Решение содержит незначительные ошибки, пробелы в обоснованиях, но в целом верно и может стать полностью правильным после небольших исправлений или дополнений.
	Указано, что Петя вспомнил про ручку в 5 минутах ходьбы от дома.
2-3	Найдено на сколько минут Петя потратит больше из-за возвращения домой.
	Рассмотрены отдельные важные случаи при отсутствии решения (или при ошибочном решении).
	Решение неверное, продвижения отсутствуют.
	Решение отсутствует.

Задача № 6. Четыре одинаковых игральных кубика сложены, как показано на рисунке. Сколько точек на самой нижней грани?Ответ объясните.

Решение:

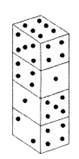
Ответ: Шесть.

Баллы	Правильность (ошибочность) решения
	Полное верное решение.
	Решение неверное, продвижения отсутствуют.
	Решение отсутствует.