Распредеденность терминов в суждениях

В логических операциях с суждениями возникает необходимость установить,

распределены или не распределены его термины — субъект и предикат.

Термин считается распределенным, если он взят в полном объеме. Термин считается

Нераспределенным, если он взят в части объема.

Рассмотрим, как распределены термины в суждениях А, Е, I, О.

Суждение А (Все S суть Р). «Все студенты нашей группы (S) сдали

экзамены (Р)». Субъект распределен, он взят в полном объеме: речь идет обо всех

студентах нашей группы. Предикат этого суждения не распределен, так как в нем

мыслится только часть лиц, сдавших экзамены, совпадающая со студентами нашей

группы.

Таким образом, в общеутвердительных суждениях S распреде­лен, а Р не

распределен. Однако в общеутвердительных суждениях, субъект и предикат

которых имеют одинаковый объем, распределен не только субъект, но и предикат.

К таким суждениям относятся общевыделяющие суждения, а также определения,

подчиняющиеся правилу соразмерности.

Суждение Е (Ни одно S не есть Р). «Ни один студент нашей группы

(S) не является неуспевающим (Р)». И субъект, и предикат взяты в полном объеме.

Объем одного термина полностью исключа­ется из объема другого: ни один студент

нашей группы не входит в число неуспевающих, и ни один неуспевающий не является

студен­том нашей группы. Следовательно, в общеотрицательных суждени­ях и S, и Р

распределены.

Суждение I (Некоторые S суть Р). «Некоторые студенты нашей группы

(S) — отличники (Р)». Субъект этого суждения не распре­делен, так как в нем

мыслится только часть студентов нашей груп­пы, объем субъекта лишь частично

включается в объем предиката. Но и объем предиката лишь частично включается в

объем субъекта: не все, а только некоторые отличники — студенты нашей группы.

Следовательно, в частноутвердительном суждении ни S, ни Р не распределены.

Суждение О (некоторые S не суть Р). «Некоторые студенты

нашей группы (S) — не отличники (Р)». Субъект этого суждения не распределен,

пре­дикат распределен, в нем мыслятся все отличники, ни один из кото­рых не

включается в ту часть студентов нашей группы, которая мыслится в субъекте.

Следовательно, в частноотрицательном сужде­нии S не распределен, а Р

распределен.

В-17

Логические отношения между суждениями

Простые суждения

Несравнимыми среди простых являются суждения, имеющие различные

субъекты или предикаты. Таковы, например, два суждения: «Среди космонавтов есть

летчики»; «Среди космонавтов есть

женщины».

Сравнимьши являются суждения с одинаковыми субъектами и

предикатами и различающиеся связкой или квантором. Обычно их называют

суждениями одинаковой материи. Например: «Все амери­канские индейцы живут в

резервациях»; «Некоторые американские индейцы не живут в резервациях».

Отношения между простыми суждениями обычно рассматрива­ются с помощью

мнемонической схемы, называемой логическим квадратом. Его

вершины символизируют простые катего­рические суждения — А, Е, I, О; стороны и

диагонали — отношения между суждениями.

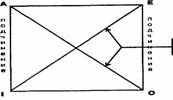Противоположность (контрарность) Частичная совместимость (субконтрарность)

Противоречие (контрадикторность)

Среди сравнимых различают совместимые и несовместимые суждения.

К совместимым относятся суждения, которые одновременно могут быть

истинными. Различают три вида совместимости: 1) эк­вивалентность

(полная совместимость), 2) частичная совмести­мость

(субконтрарность) и 3) подчинение.

1. Эквивалентными являются такие суждения, которые имеют одинаковые

логические характеристики: одинаковые субъ­екты и предикаты, однотипную

— утвердительную или отрицатель­ную — связку, одну и ту же выраженную квантором

количественную характеристику. С помощью логического квадрата отношения между

простыми эквивалентными суждениями не иллюстрируются.

2. Частичная совместимость характерна для суждений I u О, которые могут