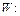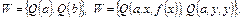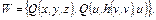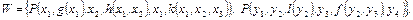Теоретико-модельная семантика логических программ
C.Н. ВАСИЛЬЕВ
ОСНОВАНИЯ ЛОГИЧЕСКОГО
ПРОГРАММИРОВАНИЯ
О Г Л А В Л Е Н И Е
Введение
§ 1. Логические программы
§ 2. Теоретико-модельная семантика логических программ
§ 3. Алгоритм унификации
§ 4. Наименьшая эрбрановская модель
§ 5. Обоснование метода ВЛП-резолюции
§ 6. Независимость правила выбора
§ 7. О процедурах ВЛП-опровержения
Заключение
Использованная литература
Введение
Автоматизация дедуктивных и других логических построений представляет собой одно из наиболее
важных направлений того раздела кибернетики, за которым закрепилось наименование «искусственный интеллект» (ИИ) [1]. Многие другие направления исследований в области ИИ, нацеленные, например, на создание так называемых экспертных систем, «интеллектуальных» баз данных, систем поддержки рассуждений по умолчанию (default reasoning), систем объяснения наблюдений, в том числе в проблематике диагностики и т.д., также стимулировали появление и развитие логического программирования.
Оказалось, что традиционные языки программирования (типа ФОРТРАН, АЛГОЛ, ПЛ-1 и др.) недостаточно эффективны при создании экспериментальных систем ИИ, прежде всего, из-за необходимости исчерпывающего описания на этих языках алгоритма решения всей задачи. Этот недостаток был замечен на фоне результатов по автоматическому доказательству теорем, возбудивших надежду на возможность разработки языков программирования весьма высокого уровня, требующих от пользователя, в основном, описания того, ЧТО нужно сделать (т.е. требующих формулировки задачи: ДАНО …, ТРЕБУЕТСЯ …), а не того, КАК это делается.
В начале 70-х гг. ХХ в. Р. Ковальским и А. Колмерауром была высказана идея, что классическая логика (а именно язык исчисления предикатов) может быть использована как язык программирования. До этого логика использовалась лишь как язык утверждений (спецификаций) либо как дедуктивный аппарат, например, в вопросно-ответных системах. Явное указание возможности процедурной интерпретации языка логики привело к созданию языков программирования типа ПРОЛОГ (PROgramming in LOGic – программирование в логике), и первый PROLOG-интерпретатор бы создан в 1972 г.
ПРОЛОГ нашел ряд приложений в задачах ИИ, послужив в начале 80-х гг. ХХ в. [18] одной из причин сверхоптимистических прогнозов в отношении вычислительных систем 5-го поколения, а сегодня, как это часто бывает, «на волне популярности» его характеристики, в том числе и недостатки (см. Заключение), часто неоправданно распространяют на логический подход (к ИИ) в целом. Не следует путать ПРОЛОГ с вообще логическим программированием, а последнее – с логическим подходом к программированию. ПРОЛОГ основывается на логическом программировании примерно как ЛИСП – на 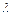 -исчислениях, а логическое программирование – лишь одно направление в том широком фронте исследований, который называется логическим подходом к программированию.
-исчислениях, а логическое программирование – лишь одно направление в том широком фронте исследований, который называется логическим подходом к программированию.
Новое дыхание логическому подходу в целом придаёт разработка исчисления позитивно-образованных формул [19]. Наконец, в качестве настольной рекомендуется книга [22] – прекрасное учебное пособие, прежде всего, тем, кто, уже имея понятие о программировании (самостоятельно либо по школе), намерен стать профессионалом в области информационных технологий. Книга [22] по-настоящему будит мысль читателя.
Применение механизмов дедукции логического программирования разнообразны; например, оно является базой так называемого абдуктивного программирования, ориентированного на автоматическое программирование гипотез [23 – 28].
Указания рекомендуются студентам III – V курсов при изучении спецкурса «Методы искусственного интеллекта и принятия решений». Более подробное изложение ПРОЛОГа см. также в [20, 21].
Логические программы
Определим синтаксис логических программ. Термы и атомы (т.е. атомарные или элементарные формулы) определяются как в языке исчисления предикатов (первого порядка) [2, 3]. Неформально говоря, термы – это переменные, константы и выражения вида 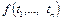 , где каждое
, где каждое 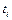 – терм, а
– терм, а 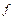 –
–  - арный функциональный символ. Атом – это всякое выражение вида
- арный функциональный символ. Атом – это всякое выражение вида 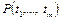 , где
, где 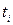 – термы,
– термы, 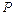 –
– 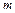 - арный предикатный символ.
- арный предикатный символ.
Дизъюнктомназывается всякое выражение вида 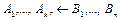 , где
, где 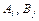 – атомы
– атомы 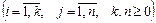 .
.
Декларативная семантика дизъюнктов (т.е. их содержательный, пока непроцедурный, смысл) совпадает с теоретико-модельной семантикой отвечающих им формул логики.
В языке исчисления предикатов дизъюнкту 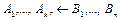 отвечают, например, формулы вида
отвечают, например, формулы вида
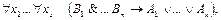 (1)
(1)
или
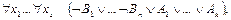 (2)
(2)
или
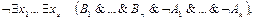 (3)
(3)
где 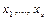 – все переменные рассматриваемого дизъюнкта. Если, в частности,
– все переменные рассматриваемого дизъюнкта. Если, в частности, 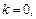 то имеем так называемую цель (целевой дизъюнкт)
то имеем так называемую цель (целевой дизъюнкт) 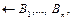 которой отвечают, например, формулы
которой отвечают, например, формулы
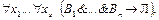
или
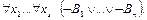
или
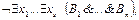
где Л – тождественно ложный предикат.
Если 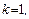 дизъюнкт называется программным(
дизъюнкт называется программным( 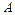 – заголовок,
– заголовок, 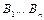 – тело дизъюнкта). Если к тому же
– тело дизъюнкта). Если к тому же 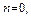 то программный дизъюнкт называется фактом. Если
то программный дизъюнкт называется фактом. Если 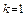 и
и 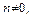 то программный дизъюнкт называется правилом (редуктором).
то программный дизъюнкт называется правилом (редуктором).
Хорновские дизъюнкты – это дизъюнкты, у которых 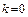 или
или 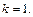 При
При 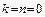 имеем пустой дизъюнкт, обозначаемый □ (в логике ему отвечает предикат Л).
имеем пустой дизъюнкт, обозначаемый □ (в логике ему отвечает предикат Л).
Справедливы включения понятий, представленные на рис. 1.
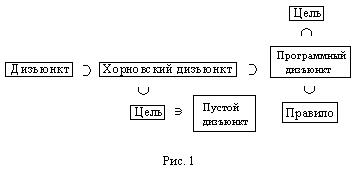
Логической программой  (или просто программой, поскольку программы в другом смысле рассматриваться не будут) называется всякое конечное (непустое) множество программных дизъюнктов.
(или просто программой, поскольку программы в другом смысле рассматриваться не будут) называется всякое конечное (непустое) множество программных дизъюнктов.
Программа  может мыслиться как набор нелогических (собственных) аксиом теории первого порядка, а цель – как отрицание формулы
может мыслиться как набор нелогических (собственных) аксиом теории первого порядка, а цель – как отрицание формулы
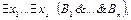 (4)
(4)
логическая выводимость которой из аксиом программы нас интересует. Эта выводимость, очевидно, будет иметь место тогда и только тогда, когда из аксиом программы  и формулы цели, т.е.
и формулы цели, т.е. 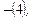 выводимо противоречие Л. Именно на опровержение (на доказательство «от противного») и ориентировано большинство известных систем автоматического доказательства теорем.
выводимо противоречие Л. Именно на опровержение (на доказательство «от противного») и ориентировано большинство известных систем автоматического доказательства теорем.
При решении задач нас может интересовать не просто то, что формула (4) является теоремой теории, отвечающей рассматриваемой программе, а чаще всего то, при каких именно значениях переменных 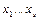 справедливо
справедливо 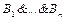 (назначением баз данных обычно является выдача даже всех таких наборов значений
(назначением баз данных обычно является выдача даже всех таких наборов значений 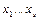 ).
).
Пример 1. Пусть дана программа 
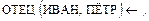 (5)
(5)
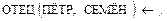 (6)
(6)
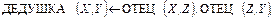 (7)
(7)
где ОТЕЦ, ДЕДУШКА – два предикатных символа, ИВАН, ПЕТР – константы, 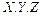 – переменные. Задание программе цели
– переменные. Задание программе цели
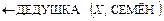 (8)
(8)
означает желание получить ответ на вопрос «Кто является дедушкой Семёна?» на основе описания предметной области (отец отца всякого человека является дедушкой этого человека) и реального состояния объектов, функций и отношений, входящих в эту область ,отцом Петра является Иван, а отцом Семёна – Пётр).
Программе  из примера 1 отвечает теория первого порядка с тремя собственными аксиомами (5), (6) и
из примера 1 отвечает теория первого порядка с тремя собственными аксиомами (5), (6) и
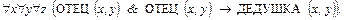 (9)
(9)
Мы можем установить выводимость в этой теории формулы 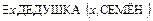 путем вывода противоречия в теории, которая отличается от упомянутой лишь дополнительно введённой аксиомой
путем вывода противоречия в теории, которая отличается от упомянутой лишь дополнительно введённой аксиомой
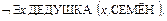 (10)
(10)
отвечающей цели (8).
Упражнения:
1. Какой частный вид примут формулы (1 – 3) для фактов?
2. Постройте в теории первого порядка [2, 3] с собственными аксиомами (5), (6), (9) вывод формулы 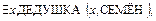 а в теории с собственными аксиомами (5), (6), (9), (10) – вывод противоречия.
а в теории с собственными аксиомами (5), (6), (9), (10) – вывод противоречия.
Теоретико-модельная семантика логических программ
Пусть пока  – произвольная формула исчисления предикатов
– произвольная формула исчисления предикатов  не обязательно «дизъюнктивная формула, т.е. не обязательно отвечает дизъюнкту [2, 3].
не обязательно «дизъюнктивная формула, т.е. не обязательно отвечает дизъюнкту [2, 3].
Для  понятия интерпретации, истинностной оценки, выполнимости, общезначимости, невыполнимости (противоречивости) модели понимаются как обычно [2, 3].
понятия интерпретации, истинностной оценки, выполнимости, общезначимости, невыполнимости (противоречивости) модели понимаются как обычно [2, 3].
В этих терминах, задавая цель 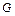 программе
программе  , мы тем самым просим показать, что множество хорновских дизъюнктов
, мы тем самым просим показать, что множество хорновских дизъюнктов 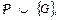 понимаемое как конъюнкция отвечающих этим дизъюнктам «хорновских» формул, невыполнимо, т.е. любая интерпретация множества
понимаемое как конъюнкция отвечающих этим дизъюнктам «хорновских» формул, невыполнимо, т.е. любая интерпретация множества 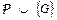 не является для него моделью.
не является для него моделью.
Оказывается, существует подкласс интерпретаций (так называемые эрбрановские интерпретации), которыми можно ограничиться при выяснении вопроса о невыполнимости формул  .
.
Введем некоторые определения.
Литерой называется атом или отрицание атома.
Выражением (в строгом смысле слова) называется терм, литера или дизъюнкт. Выражение, не содержащее переменных, называется основным выражением. Подвыражением выражения 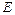 называется всякое выражение, встречающееся в
называется всякое выражение, встречающееся в 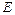 (может быть, просто совпадающее с
(может быть, просто совпадающее с 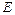 ).
).
Пусть  – формула. Эрбрановский универсум (э-универсум)
– формула. Эрбрановский универсум (э-универсум) 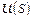 для
для  – это множество всех основных термов, которые можно построить из констант и функциональных символов, входящих в
– это множество всех основных термов, которые можно построить из констант и функциональных символов, входящих в  (если
(если  не содержит констант, то для образования термов э-универсума вводим вспомогательную константу, например, а).
не содержит констант, то для образования термов э-универсума вводим вспомогательную константу, например, а).
Пример 2. Для программы  (5) – (7) (т.е. конъюнкции формул (5), (6), (9))
(5) – (7) (т.е. конъюнкции формул (5), (6), (9)) 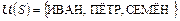 .
.
Пример 3. Для программы  вида
вида
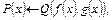
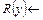
э-универсум 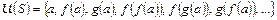 – бесконечное множество.
– бесконечное множество.
Эрбрановским базисом 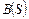 для формулы
для формулы  называется множество всех основных атомов, которые можно образовать с помощью предикатных символов из
называется множество всех основных атомов, которые можно образовать с помощью предикатных символов из  и термов из
и термов из 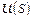 .
.
Пример 4. Для программы  из примера 3
из примера 3 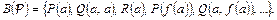 В примере 2
В примере 2 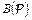 конечно.
конечно.
Интерпретация 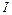 для формулы
для формулы  [2, 3] называется эрбрановской интерпретацией (э-интерпре-тацией), если:
[2, 3] называется эрбрановской интерпретацией (э-интерпре-тацией), если:
а) областью интерпретации 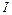 является
является 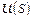 ;
;
б) константам из  в силу
в силу 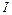 отвечают «они сами»;
отвечают «они сами»;
в) каждому  -арному функциональному символу
-арному функциональному символу 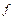 из
из  в силу
в силу 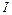 отвечает операция, которая кортежам термов
отвечает операция, которая кортежам термов 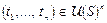 ставит в соответствие термы
ставит в соответствие термы 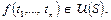
Для полного задания э-интерпретации достаточно указать подмножество из 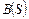 , которое состоит из всех основных атомов, объявляемых истинными в этой интерпретации. Поэтому э-интерпретации иногда отождествляются с подмножествами из
, которое состоит из всех основных атомов, объявляемых истинными в этой интерпретации. Поэтому э-интерпретации иногда отождествляются с подмножествами из 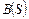 .
.
Э-интерпретация, в которой истинна (выполнима) формула  , называется эрбановской моделью для
, называется эрбановской моделью для  (э-моделью).
(э-моделью).
Теоретико-модельная (она же декларативная) семантика логических программ совпадает с теоретико-модельной семантикой соответствующих формул логики.
Пусть  – конечное множество дизъюнктов (конъюнкция дизъюнктивных формул).
– конечное множество дизъюнктов (конъюнкция дизъюнктивных формул).
Предложение 1.Если  выполнимо, то
выполнимо, то  имеет э-модель.
имеет э-модель.
Следствие 1.  невыполнимо тогда и только тогда, когда
невыполнимо тогда и только тогда, когда  не имеет э-модели.
не имеет э-модели.
Упражнения:
3. Докажите, что любая логическая программа непротиворечива (имеет модель).
4. Для формулы вида
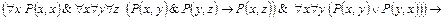
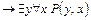
а) покажите, что любая интерпретация с конечной областью является моделью;
б) укажите интерпретацию, не являющуюся моделью.
5. Проверьте, что основной дизъюнкт  истинен в э-интерпретации I тогда и только тогда, когда хотя бы при одном
истинен в э-интерпретации I тогда и только тогда, когда хотя бы при одном 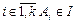 , или хотя при одном
, или хотя при одном 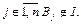
6.На примере формулы  вида
вида 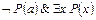 убедитесь, что для произвольных формул
убедитесь, что для произвольных формул  предложение 1 и следствие 1 несправедливы.
предложение 1 и следствие 1 несправедливы.
Алгоритм унификации
Для преобразования одних выражений в другие (как правило, более частные в содержательном смысле) служат подстановки.
Подстановка– это любое конечное множество 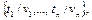 где
где 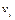 – попарно различные переменные,
– попарно различные переменные, 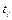 – термы и при каждом
– термы и при каждом 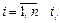 отлично от
отлично от 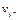 Если все
Если все 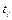 – основные термы, то подстановка называется основной. Чистая подстановка – это подстановка, в которой все
– основные термы, то подстановка называется основной. Чистая подстановка – это подстановка, в которой все 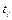 суть переменные.
суть переменные.
Пусть 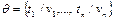 – подстановка,
– подстановка, 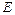 – выражение (или множество выражений). Через
– выражение (или множество выражений). Через 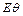 обозначается результат одновременной замены в
обозначается результат одновременной замены в 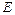 всех вхождений
всех вхождений 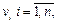 на
на 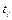 .
. 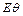 называется примером выражения
называется примером выражения 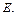
Если все переменные из 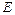 встречаются в множестве
встречаются в множестве 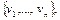 то
то 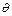 называется подстановкой для всех переменных выражения
называется подстановкой для всех переменных выражения 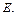 При этом если
При этом если 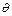 – основная подстановка, то
– основная подстановка, то 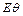 называется основным примеромвыражения
называется основным примеромвыражения 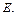
Если 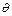 – чистая подстановка для всех переменных, выражения
– чистая подстановка для всех переменных, выражения 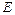 и
и 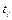 попарно различны, то
попарно различны, то 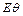 называется вариантом выражения
называется вариантом выражения 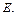
Пусть 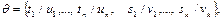
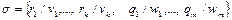 – подстановки, где
– подстановки, где 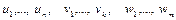 попарно различны. Тогда композицией
попарно различны. Тогда композицией 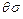 этих подстановок называется подстановка, получающаяся из множества
этих подстановок называется подстановка, получающаяся из множества
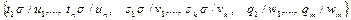
Вычеркиванием элементов 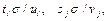 у которых
у которых 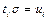 или
или 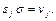
Пример 5. Пусть 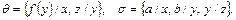 Тогда
Тогда 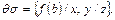
Подстановка 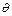 называется унификатором множества выражений
называется унификатором множества выражений 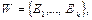 если
если 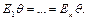 При этом
При этом 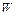 называется унифицируемым.
называется унифицируемым.
Пример 6. Множество 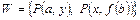 унифицируемо, так как подстановка
унифицируемо, так как подстановка 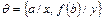 является его унификатором:
является его унификатором: 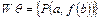 (одноэлементное множество.
(одноэлементное множество.
Унификатор 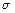 называется наиболее общим унификатором (ноунификатором) для
называется наиболее общим унификатором (ноунификатором) для 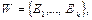 если для любого унификатора
если для любого унификатора 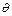 множества
множества 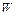 существует подстановка
существует подстановка 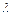 такая, что
такая, что 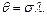
Для непустого множества выражений 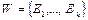 определим множество рассогласований
определим множество рассогласований 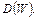 Оно получается выявлением первой (слева) позиции, на которой не для всех выражений из
Оно получается выявлением первой (слева) позиции, на которой не для всех выражений из 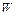 стоит один и тот же символ, и затем выписыванием из каждого выражения
стоит один и тот же символ, и затем выписыванием из каждого выражения 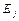 того подвыражения, которое начинается с символа, занимающего эту позицию. Множество выписанных выражений и есть
того подвыражения, которое начинается с символа, занимающего эту позицию. Множество выписанных выражений и есть 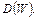
Пример 7. В множестве 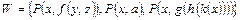 рассогласование начинается с 5-й позиции и
рассогласование начинается с 5-й позиции и 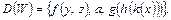
Алгоритм унификации множества выражений 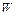 :
:
1. Полагаем 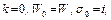 где
где 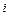 – пустая подстановка.
– пустая подстановка.
2. Если 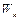 – одноэлементное множество, то останавливаемся, и подстановка
– одноэлементное множество, то останавливаемся, и подстановка 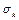 есть искомый но-унификатор для
есть искомый но-унификатор для 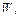 иначе строим
иначе строим 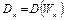
3. Если в 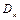 содержатся элементы
содержатся элементы 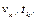 такие что
такие что 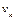 – переменная,
– переменная, 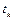 – терм и
– терм и 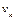 не встречается в
не встречается в 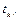 то переходим на шаг 4. В противном случае останавливаемся, заключая, что
то переходим на шаг 4. В противном случае останавливаемся, заключая, что 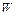 не унифицируемо.
не унифицируемо.
4. Полагаем, что 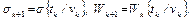
5. Полагаем 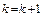 и переходим на шаг 2.
и переходим на шаг 2.
Пример 8. Если 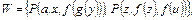 то по алгоритму получается но-унификатор
то по алгоритму получается но-унификатор
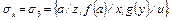
Пример 9. Если 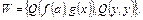 то получается, что
то получается, что 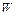 не унифицируемо.
не унифицируемо.
Теорема 1 [4]. Для любого конечного (непустого) множества 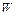 алгоритм унификации всегда заканчивает работу, причем если
алгоритм унификации всегда заканчивает работу, причем если 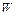 не унифицируемо, то – на шаге 3, если же
не унифицируемо, то – на шаге 3, если же 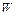 унифицируемо, то – на шаге 2, и последнее
унифицируемо, то – на шаге 2, и последнее 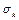 есть но-унификатор для
есть но-унификатор для 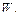
Доказательство теоремы 1 можно найти в монографии [5].
Упражнения:
7. Постройте композицию подстановок
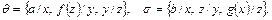
8. Пусть 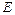 – произвольное выражение,
– произвольное выражение, 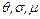 – любые подстановки. Докажите свойства подстановок:
– любые подстановки. Докажите свойства подстановок:
а) 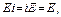
б) 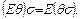
в) 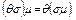
9. Пусть 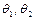 – подстановки и существуют подстановки
– подстановки и существуют подстановки 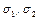 такие, что
такие, что 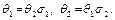 Показать, что существует чистая подстановка
Показать, что существует чистая подстановка 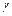 такая, что
такая, что 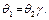
10. Доказать, что множество 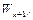 которое строится по алгоритму унификации, совпадает с множеством
которое строится по алгоритму унификации, совпадает с множеством 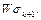
11. Выяснить унифицируемость, а в случае унифицируемости найти но-унификатор множества