Теорема (вторая e-теорема)

а) Если y – формула языка L, то вывод 墢 y существует тогда и только тогда в L¢¢, когда существует вывод å y в L

б) Теория å непротиворечива, если и только если непротиворечива теория 墢.

Метод резолюций Робинсона

В предыдущем разделе мы научились приводить формулы к виду, пригодному для применения метода автоматического доказательства теорем, предложенного в 1965 году Робинсоном.

Задача ставится так: заданы язык первого порядка L и конечное множество аксиом å. Требуется найти вывод å q для произвольной формулы q.

Она решается методом резолюций. Идею этого метода продемонстрируем сначала для случая, когда L – исчисление высказываний с множеством пропозициональных символов Р.

Алфавит исчисления состоит из элементов множества P и символов констант 0 (ложь) и 1 (истина), а также логических символов (, ), &, Ú, Ø.

Формулы определяются по индукции

1. Каждый символ из P – формула.

2. Константы 0 и 1 – формулы.

3. Если A и B – формулы, то (A&B), (AÚB), (ØA) – формулы.

Аксиомы.

(R1) Ø0 = 1,

(R2) A & B = B & A, A Ú B = BÚA,

(R3) A &1 = A, A Ú 1 = 1, A & 0 = 0, A Ú 0 = A,

(R4) Ø(A & B) = ØA Ú ØB, Ø(A Ú B) = ØA & ØB,

(R5) A & (B Ú C) = (A & B) Ú (A & C), A Ú (B & C) = (A Ú B) & (A Ú C),

(R6) ØØA = A,

Правила вывода.Напомним, что для каждого символа А Î Р символы А и ØА называются литералами. Клоусом, или дизъюнктом называется дизъюнкция литералов .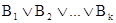

Если D₁ и D₂ – дизъюнкты, для которых существуют такие дизъюнкты 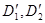и литерал В, что 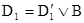и 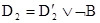, то формула:

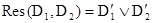
называется резольвентой D₁ и D₂. Таким образом, имеем

правило конъюнкции 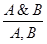(Con) и правило резолюции 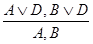(Res)

Предположим, что требуется доказать вывод q₁, q₂, …, q_n q. Сведём задачу к доказательству противоречивости формулы q₁ & q₂ & …& q_n & Øq. Приведём последнюю к конъюнктивной нормальной форме. Получим конъюнкцию некоторых дизъюнктов, составляющих список:

D₁, D₂, …, D_k.

Далее в цикле перебираем пары дизъюнктов из этого списка, находим резольвенты 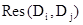и добавляем эти резольвенты, которые, очевидно, будут дизъюнктами, в конец списка. Если в списке появится 0, то вывод доказан. Если новые дизъюнкты не могут быть построены, то вывода нет.

Пример 1

Пусть требуется установить выводимость a ® b a Ú c ® b Ú c. Преобразуем в формулу высказываний, заменяя импликацию по формуле A®Bº ØAÚB. Получим формулу: Øa Ú b Ø(a Ú c) Ú b Ú c, которую надо доказать. Будем доказывать противоречивость конъюнкции дизъюнктов:

Øa Ú b, a Ú c, Øb, Øc.

Так как 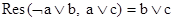, то к списку добавляется дизъюнкт b Ú c. Затем добавим 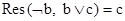. Получим список:

Øa Ú b, a Ú c, Øb, Øc, b Ú c, с.

Теперь Res (Øc, с) = 0 даёт противоречие. Значит, выводимость имеет место.

Рассмотрим теперь метод резолюций для нахождения вывода в исчислении предикатов. Мы видели, что можно предполагать формулы q и аксиомы из å, не имеющими кванторов. Для любых двух атомных формул Р(s₁, …, s_m) и Q(t₁, …, t_n) их наибольший общий унификатор h определён, если и только если P = Q, m = n, и система уравнений s₁ = t₁, s₂ = t₂, …, s_n = t_n унифицируема. Литералами в исчислении предикатов называются атомные формулы и их отрицания. Дизъюнкт определяется как дизъюнкция литералов. Два дизъюнкта D₁ и D₂ называются резольвируемыми, если существуют литералы B₁ и B₂, которые имеют наибольший общий унификатор и 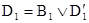, 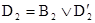для некоторых дизъюнктов 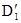и 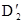. В этом случае резольвента определяется как

.

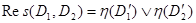Здесь h(D) – результат подстановки h в дизъюнкт D, определённый как h(R(t₁, …, t_n)) =
= R(ht₁, …, ht_n) для атомных формул, h(ØR) = Øh(R) для литералов, и h(B₁ Ú … Ú B_n)=
=h(B₁) Ú … Ú h(B_n) для дизъюнктов.

Алгоритм доказательства выводимости q₁, q₂, …, q_m q, в предположении, что q и q_i, 1 £ i £ m, не имеют кванторов, будет следующим:

1) формулу q₁ & …& q_m & Øq переводим в конъюнкцию дизъюнктов D₁&D₂&…&D_n, и переменные переименовываются таким образом, что D_i и D_j не содержат одинаковых переменных при i ¹ j;

2) устанавливаем множество дизъюнктов: F = {D₁, D₂, …, D_n}.

3) если среди элементов из F нет резольвируемых, то выводимость не имеет места, заканчиваем работу;

4) если 0 Î F, то F противоречиво, а выводимость имеет место, заканчиваем работу;

5) берём резольвируемые дизъюнкты D_i и D_j из F, устанавливаем:

F = F È {Res (D_i, D_j)}

(этот шаг включает унификацию некоторых литералов), переходим к шагу 3.

Следующий пример принадлежит Робинсону.

Пример 2

Докажем выводимость P(a, b), Q(z) P(xy) & Q(y). После переноса правой части в левую часть получаем множество дизъюнктов:

F = {P(ab), Q(z), ØP(xy) Ú ØQ(y)}.

Наибольший общий унификатор для P(ab) и P(xy) равен: {a = x, b = y}.

Добавим к F резольвенту:

Res (P(ab), ØP(xy) Ú ØQ(y)) = ØQ(y).

Имеем: F = {P(ab), Q(z), ØP(xy) Ú ØQ(y), ØQ(y)}. Резольвента Res (Q(z), ØQ(y)) = 0 приводит к противоречивости F. Стало быть, выводимость имеет место. Легко видеть, что для данного примера существуют другие пути применения метода резолюций.

Существуют различные модификации метода резолюций.

В методе резолюций участвует также правило склейки, оно позволяет из дизъюнкта R(s₁, …, s_n) Ú R(t₁, …, t_n) Ú B₁ Ú … Ú B_m получить h(R(s₁, …, s_n) Ú B₁ Ú … Ú B_m), (а из дизъюнкта ØR(s₁, …, s_n) Ú ØR(t₁, …, t_n) Ú B₁ Ú … Ú B_m – дизъюнкт
h(ØR(s₁,…, s_n)Ú Ú B₁ Ú … Ú B_m)) , где h – наибольший общий унификатор системы уравнений s₁ = t₁, …, s_n = t_n.

Нечеткая логика

Многие понятия, определяемые с помощью человеческого языка, являются расплывчатыми. Например, попытка дать определение кучи камней приводит к следующей антиномии: «Один или два камня – не куча; с другой стороны, если из кучи удалить камень, то куча останется».

Л. Заде предложил приписывать объектам степень выполнения определяемого свойства, принимающую значения в единичном интервале [0, 1]. Эта идея была положена в основу теории нечетких множеств. Она позволила моделировать человеческие рассуждения и операции над нечеткими свойствами объектов.

Нечеткие множества

Пусть U – произвольное множество. Будем рассматривать его подмножества и U будем называть универсумом. Каждое подмножество описывается с помощью свойств его элементов. Например, в универсуме натуральных чисел w подмножество
{0, 1, 2, 3, 4, 5} задаётся как

A = {n Î w: n £ 5}.

Его можно определить с помощью характеристической функции 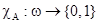, принимающей значения:

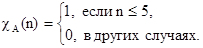
Проблема возникает при попытке определения подмножества чисел, указывающих значение возраста, при которых человек считается старым.

Пусть [0, 1] = {r Î R : 0 £ r £ 1} – единичный отрезок действительных чисел.

Определение. Нечетким множеством m на универсуме U называется произвольная функция m : U ® [0, 1]. Множество всех нечетких множеств на U обозначается через F(U).

Заметим, что часто понятия нечёткого множества и определяющей его функции различают. В этом случае, говоря о нечётком множестве A, имеют в виду функцию 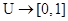. Обозначают эту функцию через 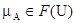и называют её функцией принадлежности.

Значение m(x) называется степенью принадлежности x нечеткому множеству m. Например, нечеткое множество «старый» определяется как функция 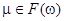, для которой m(70) = 1, а m(0) = 0, ибо ясно, что человек семидесяти лет является старым, а не достигнувший одного года младенец – нет. Можно считать, что m(20) = 0. Возрасту 45 лет можно приписать значение m(45) = 0.5, и далее продолжить функцию m линейно на интервале [20, 70].