Основные теоретические положения
Обработка входной информации Х в выходную Y в любых схемах ЭВМ обеспечивается преобразователями или цифровыми автоматами двух видов: комбинационными схемами и схемам с памятью.
Комбинационные схемы (КС) — это схемы, у которых выходные сигналы
Y = (у1, у2,..., уm) в любой момент дискретного времени однозначно определяются совокупностью входных сигналов Х = (х1, х2..., хп), поступающих в тот же момент времени t. Реализуемый в КС способ обработки информации называется комбинационным потому, что результат обработки зависит только от комбинации входных сигналов и формируется сразу же при поступлении входных сигналов. Поэтому одним из достоинств комбинационных схем является их высокое быстродействие. Преобразование информации однозначно описывается логическими функциями вида Y = f(X). Значение функции различно для разных комбинаций входных переменных и может быть задано с помощью специальной таблицы - Таблицы истинности. В левой части этой таблицы перечислены всевозможные комбинации входных переменных (наборы значений), а в правой - возможные реакции выходных сигналов. По данной таблице нетрудно составить аналитическое выражение (зависимость) для функции. Для этого наборы переменных, на которых функция принимает значение единицы, записываются как конъюнкции (логическое умножение) и связываются знаками логического сложения. Такие формы функций получили название дизъюнктивных нормальных форм (ДНФ). Если в этих функциях конъюнкции содержат все без исключения переменные в прямом или инверсном значении, то такая форма функций называется совершенной.
Алгебра логики устанавливает правила формирования логически полного базиса простейших функций, из которых могут строиться любые более сложные. Наиболее привычным базисом является набор трех функций {инверсия - [ , дизъюнкция - v, конъюнкция - л или &}. Работа с функциями, представленными в этом базисе, очень похожа на использование операций обычной алгебры.
Алгебра логики устанавливает, что существуют и другие комбинации простейших логических функций, обладающих свойством логической полноты. Например, наборы логических функций {инверсия, дизъюнкция} и {инверсия, конъюнкция} также являются логически полными. Наиболее интересны минимальные базисы, включающие по одной операции {«отрицание дизъюнкции» - Стрелка Пирса} и {«отрицание конъюнкции» - штрих Шеффера}.
Логическое выражение функции, получаемое на основе Таблицы истинности в виде совершенной дизьюнктивной формы, может быть упрощено путем его минимизации.
По упрощенным выражениям можно построить техническое устройство, имеющее минимальные аппаратные затраты.
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 57 |
| КР 15.02.07 09 00 00 ПЗ |
Рассмотрим последовательность действий минимизации логических функций на примере.
Найти минимальную дизъюнктивную форму функции Y=f(x1, x2, x3), заданной таблицей истинности
Таблица истинности функции Y=f(x1, x2, x3)
| x1 | x2 | x3 | Y | ||||||||
|
| |||||||||||
По данным таблицы запишем аналитическое выражение:
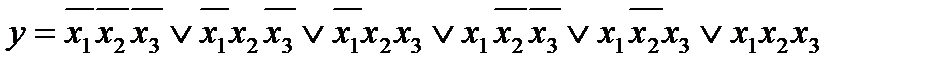
Пунктирными линиями в этом выражении отмечены пары конъюнкций, к которым можно применить операцию склеивания типа xvFx-F . Особенно хорошо это видно при использовании диаграммы Вейча, в которой «склеиваемые» конъюнкции находятся по соседству друг с другом. Диаграмма Вейча просто по-другому интерпретирует таблицу истинности (табл. 2.7).
Диаграмма Вейча функцииу
После выделения конъюнкций (они отмечены звездочкой), видно, какие конъюнкции могут образовывать пары для склеивания.
У данной функции существует пять безызбыточных дизъюнктивных форм, из которых только две являются минимальными. Одну из них можно получить, если взять пары для склеивания как указано на диаграмме Вейча. В результате получается минимизированное логическое выражение:
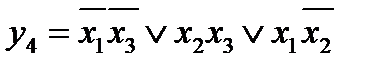
В соответствии с полученным минимизированным логическим выражением строится функциональная электрическая схема.
Признаком комбинационной схемы является отсутствие цепей обратной связи. Примерами комбинационных схем являются: сумматоры, схемы сравнения и преобразования кодов, шифраторы, дешифраторы, мультиплексоры, демультиплексоры и большинство арифметических устройств.
Комбинационная схема строится на основе логических элементов, реализующих функции алгебры логики. Число входов таких элементов соответствует числу аргументов воспроизводимой булевой функции. Логические элементы различаются между собой видом реализуемой функции, количеством входов и выходов, технологией изготовления (электрическими параметрами).
Современные технологии позволяют изготавливать микросхемы, содержащие десятки тысяч логических элементов.
Группа интегральных микросхем (ИМС), выполненных по одинаковой или близкой технологии, имеющих сходные технические характеристики и предназначенных для совместной работы в составе средств вычислительной техники, называется серией ИМС.
Основу каждой серии ИМС составляют логические элементы (ЛЭ).
| Изм. |
| Лист |
| № докум. |
| Подпись |
| Дата |
| Лист |
| 59 |
| КР 15.02.07 09 00 00 ПЗ |
