Тема 4. Общая характеристика суждения

1. Что такое суждение?

2. Какова структура суждения?

3. Каковы виды простых суждений?

4. Что такое распределенность терминов в простых суждениях?

5. Каковы виды сложных суждений? Как устанавливать истинность сложных суждений?

1. Что такое суждение?

Суждение – это вторая после понятия форма мышления. Суждением называется форма мышления, в которой что-либо утверждается или отрицается. Примеры суждений: Все сосны являются деревьями; Некоторые люди – это спортсмены; Ни один кит – не рыба; Некоторые животные не являются хищниками и т.п. Суждение также называется высказыванием.

Рассмотрим несколько важных свойств суждения, которые также являются его отличиями от понятия.

1. Любое суждение состоит из понятий, связанных между собой. Например, если связать между собой понятия карась и рыба, то может получиться суждение: Все караси являются рыбами или Некоторые рыбы являются карасями.

2. Любое суждение выражается в форме предложения (вспомним, понятие выражается в слове или словосочетании). Однако не всякое предложение может выражать суждение. Как известно, предложения бывают повествовательными, вопросительными и восклицательными. Суждение – это форма мышления, в которой что-либо утверждается или отрицается. В вопросительных и восклицательных предложениях ничего не утверждается и не отрицается, поэтому они не могут выражать собой суждение. Повествовательное предложение, наоборот, всегда представляет какое-то утверждение или отрицание, в силу чего суждение выражается в форме повествовательного предложения.

3. Любое суждение является истинным или ложным. Если суждение соответствует действительности или реальности, оно истинное, а если не соответствует, – ложное. Например, суждение: Все розы – это цветы является истинным, а суждение: Все мухи – это птицы – ложным. Надо отметить, что понятия, в отличие от суждений, не могут быть истинными или ложными. Невозможно, например, утверждать, что понятие школа – истинное, а понятие институт – ложное, понятие звезда – истинное, а понятие планета – ложное и т.п. Но разве понятия Змей Горыныч или Кащей Бессмертный, или вечный двигатель не ложные? Нет, не ложные, эти понятия являются нулевыми, но не истинными и не ложными. Поскольку любое суждение принимает одно из двух значений – истины или лжи, – то аристотелевская формальная логика также часто называется двузначной логикой.

4. Суждения бывают простыми и сложными. Сложные суждения состоят из простых, соединенных каким-либо союзом. О простых и сложных суждениях речь пойдет далее.

2. Какова структура суждения?

Суждение – это более сложная форма мышления по сравнению с понятием. Неудивительно поэтому, что суждение имеет определенную структуру, в которой можно выделить четыре части.

1. Субъект (обычно обозначается латинской буквой S) – это то, о чем идет речь в суждении. Например, в суждении: Все учебники являются книгами речь идет об учебниках, поэтому субъектом данного суждения выступает понятие учебники.

2. Предикат (обычно обозначается латинской буквой Р) – это то, что говорится о субъекте. Например, в том же суждении: Все учебники являются книгами о субъекте (т.е. об учебниках) говорится, что они – книги, поэтому предикатом данного суждения выступает понятие книги.

3. Связка – это то, что соединяет субъект и предикат. В роли связки могут быть слова есть, является, это и т.п.

4. Квантор – это указатель на объем субъекта. В роли квантора могут быть слова все, некоторые, ни один и т.п.

Рассмотрим суждение: Некоторые люди являются спортсменами. В нем субъектом выступает понятие люди, предикатом – понятие спортсмены, роль связки играет слово являются, а слово некоторые представляет собой квантор. Если даже в каком-то суждении (выраженном в форме предложения) отсутствует связка или квантор, то они все равно подразумеваются.

Между субъектом и предикатом суждения могут быть следующие отношения.

1. Равнозначность.В суждении: Все квадраты – это равносторонние прямоугольники субъект (квадраты) и предикат (равносторонние прямоугольники) находятся в отношении равнозначности.

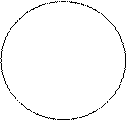
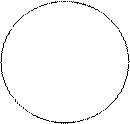2. Пересечение. В суждении: Некоторые писатели – это американцы субъект (писатели) и предикат (американцы) находятся в отношении пересечения.

S P

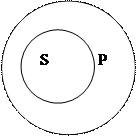
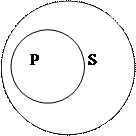
3. Подчинение.В суждении: Все тигры – это хищники субъект (тигры) и предикат (хищники) находятся в отношении подчинения, потому что представляют собой видовое и родовое понятия. Также в суждении: Некоторые хищники являются тиграми субъект (хищники) и предикат (тигры) находятся в отношении подчинения, будучи родовым и видовым понятиями.

4. Несовместимость. В суждении: Все планеты не являются звездами субъект (планеты) и предикат (звезды) находятся в отношении несовместимости.

Чтобы установить, в каком отношении находятся субъект и предикат того или иного суждения, надо сначала установить какое понятие данного суждения является субъектом, а какое – предикатом, после чего определить вид отношения между ними. Например, надо определить отношение между субъектом и предикатом в суждении: Некоторые военнослужащие являются россиянами. Сначала находим субъект суждения, – это понятие военнослужащие; затем устанавливаем его предикат, – это понятие россияне. Понятия военнослужащие и россияне находятся в отношении пересечения (военнослужащий может быть россиянином и может им не быть, и россиянин может как быть, так и не быть военнослужащим), следовательно в указанном суждении субъект и предикат пересекаются.

3. Каковы виды простых суждений?

Если в состав суждения входит один субъект и один предикат, то такое суждение является простым. Простые суждения по объему субъекта и качеству связки делятся на 4 вида. Объем субъекта может быть общим (все) и частным (некоторые), а связка может быть утвердительной (есть, или является) и отрицательной (не есть, или не является). Как видим, на основе объема субъекта и качества связки можно выделить только четыре комбинации, которыми исчерпываются все виды простых суждений (все – есть, некоторые – есть, все – не есть, некоторые – не есть). Каждый из этих видов имеет свое название и условное обозначение.

1. Общеутвердительные суждения.Как явствует из названия, это суждения с общим объемом субъекта и утвердительной связкой: Все S есть Р, например: Все школьники являются учащимися. Эти суждения обозначаются в логике латинской буквой А.

2. Частноутвердительные суждения. Название данного вида свидетельствует о том, что он представляет собой суждения с частным объемом субъекта и утвердительной связкой: Некоторые S есть Р, например: Некоторые животные являются хищниками. Эти суждения обозначаются латинской буквой I.

3. Общеотрицательные суждения – это суждения с общим объемом субъекта и отрицательной связкой: Все S не есть Р (или Ни одно S не есть Р), например: Все планеты не являются звездами (или Ни одна планета не является звездой). Такие суждения обозначаются латинской буквой Е.

4. Частноотрицательные суждения – это суждения с частным объемом субъекта и отрицательной связкой: Некоторые S не есть Р, например: Некоторые грибы не являются съедобными. Эти суждения обозначаются латинской буквой О.

4. Что такое распределенность терминов в простых суждениях?

Основные структурные элементы простого суждения – субъект и предикат – называются терминами суждения. В любом суждении каждый термин является распределеннымили нераспределенным.

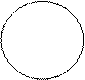
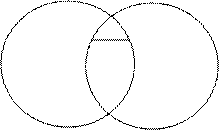
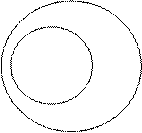
Термин считается распределенным (т.е. развернутым, исчерпанным, взятым в полном объеме), если в суждении речь идет обо всех объектах, входящих в объем этого термина, и обозначается знаком «+», а на круговых схемах Эйлера изображается полным кругом (т.е. кругом, который не содержит в себе другого круга и не пересекается с другим кругом):

+

Термин считается нераспределенным (т.е. неразвернутым, неисчерпанным, взятым не в полном объеме), если в суждении речь идет не обо всех объектах, входящих в объем этого термина, и обозначается знаком «-», а на круговых схемах Эйлера изображается неполным кругом (т.е. кругом, который содержит в себе другой круг или пересекается с другим кругом):

- - -

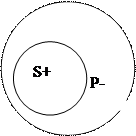
Например, в суждении: Все акулы (S) являются хищниками (Р) речь идет обо всех акулах, значит субъект этого суждения распределен. Однако, в данном суждении речь идет не обо всех хищниках, а только о части хищников (именно – о тех, которые являются акулами), следовательно, предикат указанного суждения нераспределен. Изобразив отношения между субъектом и предикатом (которые находятся в отношении подчинения) рассмотренного суждения круговыми схемами Эйлера, увидим, что распределенному термину (субъекту акулы) соответствует полный круг, а нераспределенному (предикату хищники) – неполный (попадающий в него круг субъекта как бы вырезает из него какую-то часть):

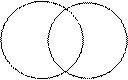
Наиболее простой способ установления распределенности терминов в простых суждениях предполагает использование круговых схем Эйлера. Достаточно уметь определять вид отношений между субъектом и предикатом в предложенном суждении и изображать их круговыми схемами. Далее еще проще – полный круг, как уже говорилось, соответствует распределенному термину, а неполный – нераспределенному. Например, требуется установить распределенность терминов в суждении: Некоторые русские писатели – это всемирно известные люди. Сначала найдем в этом суждении субъект и предикат: русские писатели – субъект, всемирно известные люди – предикат. Теперь установим, в каком они отношении. Русский писатель может как быть, так и не быть всемирно известным человеком, и всемирно известный человек может как быть, так и не быть русским писателем, следовательно субъект и предикат указанного суждения находятся в отношении пересечения. Изобразим это отношение на схеме, заштриховав ту часть, о которой идет речь в суждении:

S P

Как видим, и субъект и предикат изображаются неполными кругами (у каждого из них как бы отрезана какая-то часть), следовательно оба термина предложенного суждения нераспределены (S–, P–).

5. Каковы виды сложных суждений? Как устанавливать истинность сложных суждений?

Сложным называется суждение, в составе которого можно выделить хотя бы одно простое суждение. В зависимости от союза, с помощью которого простые суждения входят в состав сложного, выделяется, как правило, шесть видов сложных суждений.

Конъюнктивное суждениеили конъюнкция – это сложное суждение с соединительным союзом «и», который обозначается в логике условным знаком /\. С помощью этого знака конъюнктивное суждение, состоящее из двух простых суждений, можно представить в виде формулы а /\ в (читается «а и в»), где а и в – это два каких-либо простых суждения. Например, сложное суждение: Сверкнула молния, и загремел гром является конъюнктивным или конъюнкцией (соединением) двух простых суждений: 1. Сверкнула молния., 2. Загремел гром. Конъюнкция может состоять не только из двух, но и из большего количества простых суждений. Например: Сверкнула молния, и загремел гром, и пошел дождь (а /\ в /\ с).

Дизъюнктивное суждение или дизъюнкция – это сложное суждение с разделительным союзом «или». Этот союз может использоваться как в нестрогом (неисключающем) значении, так и в строгом (исключающем). Неудивительно поэтому, что дизъюнктивные суждения делятся на два вида.

Нестрогая дизъюнкция – это сложное суждение с разделительным союзом «или» в его неисключающем (нестрогом) значении, который обозначается условным знаком V. С помощью этого знака нестрогое дизъюнктивное суждение, состоящее из двух простых суждений можно представить в виде формулы а V в (читается «а или в»), где а и в – это два каких-либо простых суждения. Например, сложное суждение: Он изучает английский, или он изучает немецкий является нестрогим дизъюнктивным или нестрогой дизъюнкцией (разделением) двух простых суждений: 1. Он изучает английский., 2. Он изучает немецкий. Как видим, эти суждения друг друга не исключают, ведь возможно изучать и английский, и немецкий одновременно, в силу чего данная дизъюнкция является нестрогой.

Строгая дизъюнкция– это сложное суждение с разделительным союзом «или» в его исключающем (строгом) значении, который обозначается условным знаком V. С помощью этого знака строгое дизъюнктивное суждение, состоящее из двух простых суждений, можно представить в виде формулы а V в (читается «или а, или в»), где а и в – это два каких-либо простых суждения. Например, сложное суждение: Он учится в 9 классе, или он учится в 11 классе является строгим дизъюнктивным или строгой дизъюнкцией (разделением) двух простых суждений: 1. Он учится в 9 классе., 2. Он учится в 11 классе. Обратим внимание на то, что эти суждения друг друга исключают, ведь невозможно одновременно учиться и в 9 и в 11 классе (если он учится в 9 классе, то обязательно не учится в 11 классе и наоборот), в силу чего данная дизъюнкция является строгой. Как нестрогая, так и строгая дизъюнкция могут состоять не только из двух, но из большего числа простых суждений. Например: Он изучает английский или он изучает немецкий, или он изучает французский (а V в V с) или Он учится в 9 классе или он учится в 10 классе, или он учится в 11 классе (а V в V с).

Импликативное суждение или импликация – это сложное суждение с условным союзом «если... то», который обозначается условным знаком ®. С помощью этого знака импликативное суждение, состоящее из двух простых суждений, можно представить в виде формулы а ® в (читается «если а, то в»), где а и в – это два каких-либо простых суждения. Например, сложное суждение: Если вещество является металлом, то оно электропроводно представляет собой импликативное суждение или импликацию (причинно-следственную связь) двух простых суждений: 1. Вещество является металлом., 2. Вещество электропроводно. Как видим, в данном случае эти два суждения связаны таким образом, что из первого вытекает второе (если вещество – металл, то оно обязательно электропроводно), однако из второго не вытекает первое (если вещество электропроводно, то это вовсе не означает, что оно является металлом). Первая часть импликации называется основанием, а вторая – следствием.

Эквивалентное суждение или эквиваленция – это сложное суждение с союзом «если ... то» не в его условном значении (как в случае с импликацией), а в тождественном (эквивалентом). В данном случае этот союз обозначается условным знаком «, с помощью которого эквивалентное суждение, состоящее из двух простых суждений, можно представить в виде формулы а « в(читается «если а, то в, и если в, то а»), где а и в – это два каких-либо простых суждения. Например, сложное суждение: Если число является четным, то оно делится без остатка на 2 представляет собой эквивалентное суждение или эквиваленцию (равенство, тождество) двух простых суждений: 1. Число является четным., 2. Число делится без остатка на 2. Нетрудно заметить, что в данном случае два суждения связаны так, что из первого вытекает второе, а из второго – первое: если число четное, то оно обязательно делится без остатка на 2, а если число делится без остатка на 2, то оно обязательно четное. Понятно, что в эквиваленции, в отличие от импликации, не может быть ни основания, ни следствия, т.к. две ее части являются равнозначными суждениями.

Отрицательное суждение или отрицание – это сложное суждение с союзом «неверно, что...», который обозначается условным знаком . С помощью этого знака отрицательное суждение можно представить в виде формулы а (читается «неверно, что а»), где а – это какое-либо простое суждение. Вспомните, давая определение сложному суждению, мы говорили, что оно состоит из простых суждений, связанных каким-либо союзом, или, другими словами, сложным является суждение, в котором возможно выделить хотя бы одно самостоятельное простое суждение. В случае с отрицанием мы имеем как раз такую ситуацию, когда сложное суждение состоит не из двух или нескольких простых суждений (как в случае с конъюнкцией, дизъюнкцией, импликацией и эквиваленцией), а включает в свой состав одно самостоятельное простое суждение (а). Пример отрицательного суждения: Неверно, что все мухи являются птицами.

Союзов в естественном языке много, но все они по смыслу сводятся к рассмотренным шести видам, и любое сложное суждение относится к одному из них. Например, сложное суждение: Уж полночь близится, а Германа все нет является конъюнкцией, потому что в нем союз «а» употребляется в роли соединительного союза «и». Сложное суждение, в котором вообще нет союза: Посеешь ветер, пожнешь бурю является импликацией, т.к. два простых суждения в нем связаны по смыслу условным союзом «если…то».

Любое сложное суждение является истинным или ложным в зависимости от истинности или ложности входящих в него простых суждений. Ниже приведена таблица истинности всех видов сложных суждений в зависимости от всех возможных наборов истинностных значений двух входящих в них простых суждений (таких наборов всего четыре: 1. оба простых суждения истинные; 2. первое суждение истинное, а второе ложное; 3. первое суждение ложное, а второе истинное; 4. оба суждения ложные).

а	в	а /\в	а V в	а V в	а ® в	а « в	а
И	И	И	И	Л	И	И	Л
И	Л	Л	И	И	Л	Л
Л	И	Л	И	И	И	Л	И
Л	Л	Л	Л	Л	И	И

Как видим, конъюнкция (а /\в) истинна только тогда, когда истинны оба простых суждения, входящих в нее. Надо отметить, что конъюнкция, состоящая не из двух, а из большего количества простых суждений, также истинна только в том случае, когда истинны все входящие в нее суждения. Во всех остальных случаях она является ложной. Нестрогая дизъюнкция (аVв), наоборот, истинна во всех случаях за исключением того, когда оба входящих в нее простых суждения ложны. Нестрогая дизъюнкция, состоящая не из двух, а из большего количества простых суждений, также ложна только тогда, когда ложны все входящие в нее простые суждения. Строгая дизъюнкция (аVв) истинна только тогда, когда одно входящее в нее простое суждение истинно, а другое ложно. Строгая дизъюнкция, состоящая не из двух, а из большего количества простых суждений, истинна только в том случае, если истинно только одно из входящих в нее простых суждений, а все остальные ложны. Импликация (а ® в) ложна только в одном случае, когда ее основание является истинным, а следствие ложным. Во всех остальных случаях она истинна. Эквиваленция (а « в) истинна тогда, когда два составляющих ее простых суждения истинны или же, когда они оба являются ложными. Если одна часть эквиваленции истинна, а другая ложна, то эквиваленция ложна. Проще всего определяется истинность отрицания: когда утверждение (а) истинно, его отрицание (Øа) ложно; когда утверждение (а) ложно, его отрицание ( а) истинно.

Резюме: Суждение, или высказывание – это форма мышления, состоящая из понятий, в которой что-либо утверждается или отрицается. В любом суждении можно выделить субъект, предикат, связку и квантор. Сужения с одним субъектом и предикатом называются простыми; по объему субъекта и качеству связки они делятся на четыре вида: общеутвердительные, частноутвердительные, общеотрицательные, частноотрицательные. Субъект и предикат простого суждения могут быть распределенными или нераспределенными. Сложные суждения состоят из простых суждений, соединенных какими-либо союзами, в зависимости от которых выделяется шесть видов сложных суждений: конъюнкция, дизъюнкция строгая и нестрогая, импликация, эквиваленция, отрицание. Истинность сложных суждений зависит от истинности входящих в них простых суждений и вида логической связи между ними.

Вопросы для самопроверки

1. Что такое суждение? Чем оно отличается от понятия? Приведите, самостоятельно подобрав, пять примеров суждений.

2. Почему понятия не могут быть истинными или ложными, в отличие от суждений? Что такое двузначная логика? Какова структура суждения? Придумайте пять суждений и укажите в каждом из них субъект, предикат, связку и квантор. В каких отношениях могут быть субъект и предикат суждения? Приведите по три примера для каждого случая отношений между субъектом и предикатом: равнозначности, пересечения, подчинения, несовместимости.

3. Какие суждения называются в логике простыми? На каком основании подразделяются на виды простые суждения? Почему они делятся именно на 4 вида? Охарактеризуйте все виды простых суждений: название, структура, условное обозначение, пример.

4. Что такое термины суждения? В каком случае термин суждения считается распределенным, а в каком – нераспределенным? Как с помощью круговых схем Эйлера возможно установить распределенность терминов в простом суждении?

5. Что такое сложное суждение? На каком основании выделяются виды сложных суждений? Охарактеризуйте все виды сложных суждений: название, союз, условное обозначение, формула, пример. Чем отличается нестрогая дизъюнкция от строгой? Как отличить импликацию от эквиваленции? Каким образом возможно определить вид сложного суждения, если в нем вместо союзов «и», «или», «если… то» употребляются какие-либо другие союзы? Приведите по три примера для каждого вида сложных суждений, не используя при этом союзов «и», «или», «если…то».

6. От чего зависит истинность сложных суждений? Какие значения истинности принимают конъюнкция, нестрогая и строгая дизъюнкция, импликация, эквиваленция и отрицание в зависимости от всех наборов истинностных значений входящих в них простых суждений?

Литература

1. Гетманова А. Д. Учебник по логике. – М.: Че Ро, 2000.

2. Гусев Д. А. Логика. Учебное пособие для вузов. – М.: ЮНИТИ-ДАНА, 2004.

3. Гусев Д. А. Конспект лекций с задачами. Учебное пособие для вузов. –М.: Айрис Пресс, 2005.

4. Гусев Д. А. Логика. Учебное пособие. – М.: МПСИ, 2005.

5. Гусев Д. А. Тестовые задания и занимательные задачи по логике. – М.: МПСИ, 2003.

6. Ивин А.А. Логика. Учебное пособие. – М.: Знание, 1998.

7. Ивин А.А. Практическая логика. Задачи и упражнения. – М.: Просвещение, 1996.

8. Ивин А.А. Строгий мир логики. – М., 1988.

9. Краткий словарь по логике. – М., 1991.

10. Свинцов В. И. Логика. Элементарный курс для гуманитарных специальностей. – М., 1998.