Две формы относительного показателя динамики

ОПД =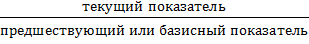

ОПД = 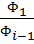ОПД =

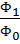
	янв	фер	март	апр	май
А
ОПД(пер)	120%	125%	133%	110%
ОПД(пост)		120%	150%	200%	220%
		220%

Произведение всех относительных показателей динамики равно

ОПД (пер) У₀ У₁ У₂ У₃ …. У_n

ОПД =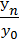

Относительный показатель планового задания

ОППЗ =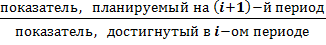

Относительный показатель реализации плана

ОПРП =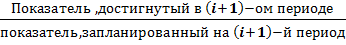

ОПРП =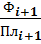

Относительный показатель структуры

ОПС = 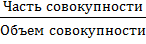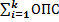*100%

Относительный показатель координации

ОПК =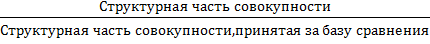

Относительный показатель интенсивности

ОПИ =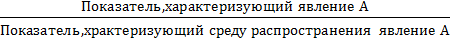

Относительный показатель уровня экономического развития

ОПУЭР = /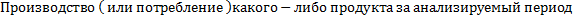

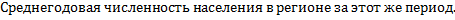
Относительный показатель сравнения

ОПС _равн.=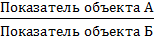

Тема 5: Статистические показатели в форме средних величин

5.1 Степенные средние

Показатель в форме средней величины:

· Представляет собой универсальную обобщающую характеристику статистической совокупности

· Отражает типичный уровень изучаемого признака

· Является центром распределения

· Используется в анализе структуры, вариации, взаимосвязи, динамики

Для неоднородной совокупности общая средняя заменяется или дополняется средними групповыми.

Важнейшее свойство – средняя отражает то общее, что присуще всем единицам исследуемой совокупности.

Отклонение значений признака, отдельных единиц совокупности обусловлены различными факторами.

Если совокупность неоднородна, то метод «среднем» используется в сочетании с методом «группировок».

Определяющее свойство средней величины

f (x₁ , x₂ , … , x_n) = f ( , , … , )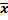

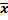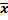X₁ – значения усредняемого признака

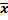– Средняя величина

Виды (формы) средних величин:

· Средняя арифметическая

· Средняя гармоническая

· Средняя геометрическая

· Средняя квадратическая

· Средняя кубическая и степенные средние более высоких порядков

Средняя степенная

=

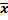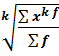
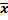– средняя

f- вес варианта признака

x – вариант осредненного признака

Использование весов при расчете средних показателей

· Невзвешенные (простые) средние

Данные не сгруппированы, т.е. представлены в виде индивидуальных значений признака.

· Взвешенные средние

Данные сгруппированы, т.е. представлены в виде дискретного или интервального ряда распределения.

· Средняя арифметическая

- невзвешенная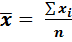

Где:

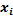–значение признака i-й единицы совокупности

n – объем совокупности

-взвешенная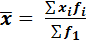

Где:

x_i –i-йвариант признака

f_i– вес i-го варианта признака

Шаги при решении задач:

1. Переход от интервального к дискретному ряду распределения, то есть замена интервала его серединой.

2. Середина интервала = верхняя граница + нижняя граница интервала делят пополам.

3. Величина открытого интервала условно приравнивается к величине середины интервала.

Свойства средней арифметической

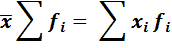
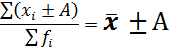
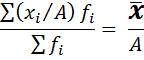
Средняя гармоническая

- невзвешенная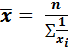

- взвешенная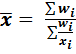

Где: 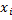- i-й вариант осредняемого признака ;

n – объем совокупности

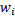– вес i-го варианта

Используется, когда известен числитель, но не известен знаменатель исходного соотношения средней.

Структурные средние

· К структурным средним относятся две основные характеристики вариационного ряда распределения – мода и медиана.

· Мода (М₀) – вариант изучаемого признака, имеющий наибольшую частоту.

· Медиана (М_е) - вариант изучаемого признака, находящийся в середине ранжированного (упорядоченного) ряда всех его значений.

· Основное свойство медианы:

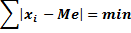
Определение моды по дискретному ряду распределения

Модальным вариантом или модой будет являться вариант, которому соответствует максимальная частота.

Определение медианы по дискретному ряду распределения

Медианным вариантом или медианой будет являться вариант, накопленная частота которого первой превышает половину сумм всех частот.

N_me =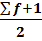

Определение моды по интервальному ряду распределения

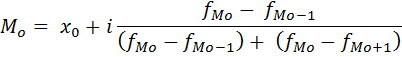
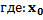–нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту);

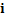− величина интервала;

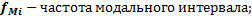
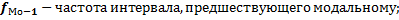
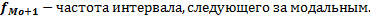
Определение медианы по интервальному ряду распределения

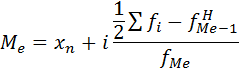
Где: x_o – нижняя граница медианного интервала ( медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот);

i – величина интервала;

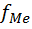– частота медианного интервала;

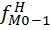– накопленная частота интервала, предшествующего медианному.

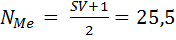
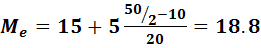(пример по таблице на лекции)

Средняя, мода и медиана в оценке асимметрии распределения

Симметричное распределение

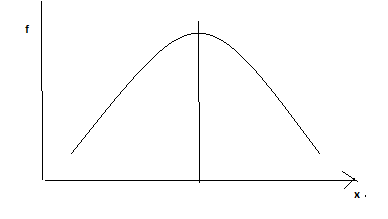
Мода, медиана и другие характеристики рядов расределения

Децили, Перцентили, x max, x min

Определение квартилей по интервальному ряду распределения

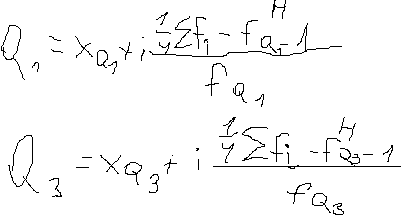
Где 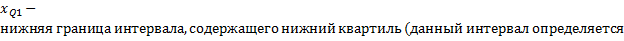по накопленной частоте, первой превышающей 25% от общей суммы частот;

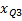- нижняя граница интервала, содержащего верхний квартиль (данный интервал определяется по накопленной частоте, первой превышающей 75% от общей суммы частот);

i – величина интервала;

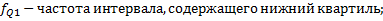
- То же для верхнего квартиля;

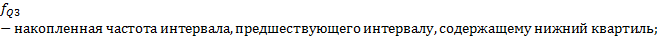
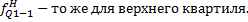
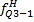
Определение децилей по интервальному ряду распределения

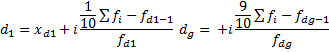
Тема 6: Анализ вариации

6.1 Основные показатели вариации

Показатели вариации позволяют оценить:

Ø Колеблемость, разброс значений признака у – единиц стат. Совокупности;

Ø Устойчивость развития изучаемых процессов во времени;

Ø Взаимосвязи между изучаемыми признаками

Ø Различного рода риски