Распределенность терминов в простых суждениях.

Один из аспектов уточнения смысла высказываний связан с установлением распределенности, либо нераспределенности его терминов (S, P).
Термин считается распределенным, если он взят или исключен в полном объеме.
Термин, взятый или исключенный частично, считается нераспределенным.
В логике принято изображать распределенность терминов при помощи таблицы и графически.

Таблица распределенности терминов:

Виды суждений Термины S P A + - E + + I - - O - +

Символ «+» обозначает распределенность термина, а символ «-» - нераспределенность.

На основании таблицы можно сформулировать ряд правил:

1. Субъект распределен в общих суждениях (А, Е) и не распределен в частных (I, O).
2. Предикат распределен в отрицательных суждениях (Е, О) и не распределен в утвердительных (A, I).
3. В частноутвердительных суждениях (I) термины, как правило, не распределены.

Для того чтобы вопрос о распределенности терминов не вызывал затруднений, нужно установить вид отношения между понятиями, выражающими субъект и предикат суждения. Это лучше сделать при помощи круговых схем:
1. Суждение А.

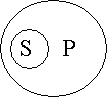Субъект S суждения А распределен, т.к. понятие S полностью подчинено по содержанию и включено по объему в понятие Р. Например: «Все треугольники – геометрические фигуры». Но не наоборот, поэтому предикат суждения А – нераспределен.

2. Суждение Е

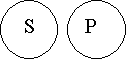Субъект S и предикат Р суждения Е – распределены, т.к. в их содержании отсутствуют какие-либо общие признаки (они несравнимы), а объемы полностью исключают друг друга. Например: «Ни на одной из акций на предъявителя не указано имя ее владельца».

3. Суждение I

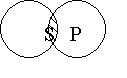Субъект S и предикат Р суждения I – не распределены, т.к. в их содержании имеется лишь часть общих признаков, а значит их объемы лишь пересекаются. Например: «Некоторые фрески хорошо сохранились».

4. Суждение О.

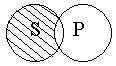Субъект S суждения О – не распределен, т.к. значительная часть его содержания отличается от содержания понятия Р, который является распределенным. Например: «Некоторые науки не являются гуманитарными».

Правила распределенности терминов позволяют судить о соотношении терминов суждения, даже не зная их содержания.

Упражнения:

1. Пользуясь логическим квадратом, установите логическое значение:
1.1. А,I,0, если Е- истинно. Е = истинно; А = ложно; О = ложно; I = ложно;
1.2. А,Е,I, если O - истинно. О = истинно; А = ложно; I = истинно; Е = ложно;
1.3. А,Е,О, если I - ложно. I = ложно; О = истинно; А = ложно; Е = истинно;

2. Определите распределенность терминов в следующих суждениях:
2.1. Некоторые выпускники вузов работают в банках. I → I
2.2. Ни один вид спорта не является легким. E → E
2.3. Все химические элементы обладают атомным весом. A → I
2.4. Некоторые постройки не являются современными. I → I
2.5. Всякий человек в душе - ребенок. A → I
2.6. Все диалоги Платона - плод философских размышлений. A → I
2.7. Некоторые автомобили являются дизельными. I → I

ТЕМА №12

"Сложные суждения".

План:

1. Образование сложных суждении.

2. Установление логического значения сложных суждений при помощи таблиц истинности.