Выводы логики высказываний.

Условно-категорические умозаключения. Это двухпосылочное умозаключение. Одна посылка является условным суждением, а вторая посылка и заключение, могут быть либо антецедентом, либо консеквентом первой посылки, либо их отрицанием.

К правильным условно-категорическим умозаключениям относятся умозаключения, имеющую следующую логическую форму:

А→ В, А

^{________________}

В

Данный способ умозаключение получил название modus ponens («утверждающий метод рассуждения»). В утверждающем способе умозаключения устанавливается отношение логического следования между посылками ( условным суждением А→ В, его антецедентом А) и заключением (консеквентом В).

Другим правильным типом условно-категорических умозаключений относятся умозаключения, имеющую следующую логическую форму:

А→ В, − В

^{___________________}

− А

Данный способ условно-категорических умозаключений называется modus tollens («отрицающий способ рассуждения»). В умозаключении данной структуры осуществляется переход от условного суждения А→ В и отрицания его консеквента − В к отрицанию антецедента − А.

Необходимо обратить внимание, что не являются правильными следующие способы условно-категорических рассуждений:

А→ В, В А→ В, − А

^{__________________} ; ^{_________________};

А − В

Разделительно-категорические умозаключения. Это двухпосылочное умозаключение. Одна из посылок - разделительное суждение ( строгая или нестрогая дизъюнкция), а другая и заключение являются одним из членов или отрицание какого-то из членов этого суждения. Основными правильными формами разделительно-категорических умозаключений являются :

А V В, − А А V В, − В

^{__________________} ; ^{____________________}
В А

Эти схемы рассуждений получили название modus tollendo ponens

( «отрицающе-утверждающий способ рассуждения»).

К неправильным относятся следующие схемы разделительно-категорических умозаключений:

А V В, А А V В, В

^{__________________} ; ^{____________________}
− В − А

Но если нестрогую дизъюнкцию заменить строгой дизъюнкцией, то схема умозаключений преобразуется в правильную форму :

А Ỳ В, А А Ỳ В,

^{__________________} ; ^{_________________} .
− В − А

При этом способе умозаключения осуществляется переход от утверждения одного из членов строгой дизъюнктивной посылки к отрицанию другого

её члена. Умозаключения, построенные по этой схеме, называются modus ponendo tollens (« утверждающе-отрицающий способ рассуждения»).

Условно-разделительные умозаключения. Эти умозаключения содержат в качестве посылок несколько условных суждений и одно разделительное суждение. Такие умозаключения называются дилеммами ( ди дважды…+ др.-гр. λήμμα предположение).

Дилеммы делятся на простые, сложные, конструктивные и деструктивные.

Схемы правильных дилемм:

А→ B, C→B, А V C

^{_____________________________ ___} простая конструктивная дилемма;

B

А→ B, C → D, А V C

^{_______________________________ __} сложная конструктивная дилемма;

B V D

A→ B, A → C, −B V −C

^{___________________________________ __} простая деструктивная дилемма;

− A

A → B, C→ D, −B V −D

^{__________________________________ __} сложная деструктивная дилемма.

−A V −C

1.4.3. Простой категорический силлогизм:

1.4.3.1. Состав простого категорического силлогизма.
1.4.3.2. Фигуры и модусы силлогизма.

1.4.3.3. Общие правила силлогизма и специальные правила фигур.

Теорию логических умозаключений из категорических суждений называют силлогистикой. Правильные силлогистические умозаключения при истинности посылок гарантируют истинность заключения.Простой категорический силлогизм–это двухпосылочное дедуктивное умозаключение, в котором из двух категорических суждений выводится третье категорическое суждение.Первые два суждения называются посылками, а третье – заключением.
Категорическое суждение включает два понятия, которые называются терминами:субъект- термин, предикат- термин.В простом категорическом силлогизме должно быть три и только три термина. Каждый термин силлогизма должен быть представлен два и только два раза. Термин, входящий в обе посылки, называется средним термином (terminus medius). Средний термин устанавливает связь между остальными двумя терминами, называемыми крайними терминами. Крайний термин, выступающий в заключении субъектом, называется меньшим термином ((terminus minor). Крайний термин, являющийся предикатом заключения, − большим термином (terminus major).

Термины силлогизма принято обозначать латинскими буквами: М – средний термин, S – меньший термин, Р – больший термин. Посылка, включающая наряду со средним термином меньший термин, называется меньшей посылкой. Соответственно, посылка, включающая наряду со средним термином больший термин, большей посылкой.

Пример категорического силлогизма:

Совершивший преступление(M), должен быть подвергнут наказанию(P)

Обвиняемый (S) – совершил преступление (M)

Обвиняемый(S) должен быть подвергнут наказанию (P)

Фигуры силлогизма. Так как правильность силлогизма зависит исключительно от его формы, чрезвычайно важно выявить эти формы правильных силлогизмов.

Силлогизмы отличаются друг от друга расположением среднего термина в структуре посылок. Эти разновидности силлогизма называются фигурами. Имеется четыре фигуры силлогизма.

В первой фигуре средний термин выступает в качестве субъекта в большей посылке и предиката в меньшей (Рис. 1.).

Во второй фигуре средний термин выступает в качестве предиката в обеих посылках (Рис. 2.).

В третьей фигуре средний термин выступает в качестве субъекта в обеих посылках (Рис.3.).

В четвертой фигуре средний термин является предикатом в большей и субъектом в меньшей посылках (Рис.4.).

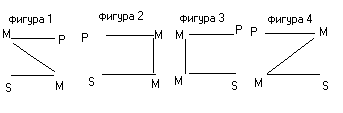
Рис.1. Рис.2. Рис.3. Рис.4.

Модусы силлогизма. Модусы – это разновидности силлогизма внутри каждой фигуры, указывающие возможные сочетания видов категорических суждений в посылках и заключении. Всего модусов 256. Так как видов категорических суждений по объединенной классификации 4, то можно посчитать, что в каждой фигуре 64 модуса (возможные сочетания видов суждений, образующих посылки и заключение силлогизма), а по четырем фигурам силлогизма – 256. Однако не все модусы являются правильными, то есть заключение с логической необходимостью следует из посылок. Правильных модусов – 24 ( по 6 модусов в каждой фигуре). Среди них выделяют 19 сильных модусов и 5 – слабых. Каждому правильному модусу еще в средневековье было присвоено имя.

Фигура 1 Фигура 2 Фигура 3 Фигура 4

Barbara, Baroko Bokardo Camenos

Celarent, Cesare Disamis Dimaris

Darii, Camestres Datisi Camenes

Ferio Festino Ferison Fresison

Barbari Camestrop Darapti Bramantip

Celaront Cesaro Felapton Fesapo

.

Последовательность гласных букв слева направо этих названий указывают вид суждений соответственно большей, меньшей посылок и заключения. Отсюда мы получим следующие сочетания видов суждений по модусам:

Фигура 1 Фигура 2 Фигура 3 Фигура 4

aaa aoo oao aeo

eae eae iai iai

aii aee aii aee

eio eio eio eio

aai aeo aai aai

eao eao eao eao

Следовательно, Barbara, модус фигуры 1, в котором обе посылки и заключение общеутвердительные суждения (этот вид суждений, как мы отмечали, обозначается латинской буквой А) имеет следующую структуру: ааа; Celarent – еае (большая посылка общеотрицательное суждение, меньшая посылка – общеутвердительное, заключение также общеотрицательное суждение)..

Общие правила и специальные правила фигур категорического силлогизма. Определены правила построения правильных категорических силлогизмов. Выполнение каждого правила является необходимым, а всех вместе достаточным основанием правильности модуса. Силлогизм правильный, если все правила, предъявляемые к нему, соблюдены, если не выполнено хотя бы одно из правил, силлогизм – неправильный.

Имеется пять правил силлогизма, которые, в свою очередь, делятся на правила терминов и правила посылок.

Правила терминов:

(1) Средний термин должен быть распределен по крайней в одной из

посылок;

(2) Если термин нераспределен в посылке, то он не должен быть

распределен в заключении;

Правила посылок:

(3) По крайней мере одна из посылок должна быть утвердительной ( из двух

отрицательных посылок нельзя сделать заключения);

(4) Из двух утвердительных посылок нельзя сделать отрицательного

заключения;

(5) Если одна из посылок отрицательное суждение, то заключение должно

быть отрицательным;

Наряду с основными правилами есть два производных:

(6) Из двух частных посылок нельзя сделать заключения ( по крайней мере

одна из посылок должна быть общим суждением);

(7) Если одна из посылок частное суждение, то и заключение должно быть

частным.

Специальные правила фигур:

Фигура 1: 1)большая посылка должна быть общим суждением;

2) меньшая посылка – утвердительной.

Фигура 2: 1) большая посылка должна общим суждением;

2) одна из посылок – отрицательным суждением.

Фигура 3: 1) меньшая посылка должна быть утвердительной;

2) одна из посылок – общим суждением;

3) заключение – всегда частное суждение.

Фигура 4 имеет искусственный характер. В истории предпринимались попытки сформулировать общие правила для нее, но они не принесли желаемых результатов. У четвертой фигуры нет общих регламентирующих специальных правил. Правильность умозаключений четвертой фигуры устанавливается по общим правилам силлогизма и правильным модусам четвертой фигуры.