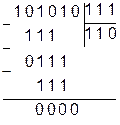Тема 1.3 Системы счисления

Система счисления (СС) – система приемов и правил, которые позволяют устанавливать взаимно однозначное соответствие между любым числом и его представлением в виде совокупности конечного числа символов.

В зависимости от способа изображения чисел с помощью цифр системы счисления делятся на позиционные и непозиционные.

В непозиционных системах любое число определяется как некоторая функция от численных значений совокупности цифр, которые представляют это число. Цифры в непозиционных системах исчисления отвечают некоторым фиксированным числам. Пример непозиционной системы – римская система исчисления.

В электронных цифровых устройствах применяются позиционные системы счисления. Позиционной системой счисления называется потому, что значение каждой входящей в число цифры зависит от ее положения в записи числа.

Любая позиционная СС с основанием q может быть представлена в виде полинома:

A_(q) = r_nqⁿ + r_n–1q^n–1 + r_n–2q^n–2 + … + r₁q¹ + r₀q⁰ + r_–1q^–1 + …,

где A – число в позиционной СС с основанием q; r_i – коэффициент; n – степень и индекс.

Позиционные СС бывают различными в зависимости от основания:

1) Десятичная с основанием 10

[0 1 2 3 4 5 6 7 8 9]

236₁₀ = 2∙10² + 3∙10¹ + 6∙10⁰

2) Восьмеричные с основанием 8

[0 1 2 3 4 5 6 7]

236₈ = 2∙8² + 3∙8¹ + 6∙8⁰ = 158₁₀

3) Шестнадцатеричная с основанием 16

[0 1 2 3 4 5 6 7 8 9 A B C D E F]

2АF₁₆ = 2∙16² + A∙16¹ + F∙16⁰ = 2∙16² + 10∙16¹ + 15∙16⁰ = 687₁₀

4) Двоичная с основанием 2

[0 1]

1011₂ = 1∙2³ +0∙2² + 1∙2¹ + 1∙2⁰ = 11₁₀

Таблица 1.3.1 – Методы перевода целых и дробных чисел в десятичную СС

Тип преобразования	Целые числа	Дробные числа
Повторное умножение промежуточного результата на q и сложение со значением разряда данного числа. Первый промежуточный результат есть старший разряд	Повторное деление промежуточного результата на q и сложение с разрядом данного числа. Первый промежуточный результат есть последний разряд, разделенный на q
Двоичное в десятичное	1∙2 + 1 = 3 3∙2 + 0 = 6 6∙2 + 1 = 13 13∙2 + 1 = 27 27∙2 + 0 = 54 54∙2 + 0 = 108   11011002 = 10810	1:2 = 0,5 (0,5 + 1):2 = 0,75 (0,75 + 0):2 = 0,375 (0,375 + 1):2 = 0,6875 (0,6875 + 0):2 = 0,34375 (0,34375 + 1):2 = 0,67187 (0,67187 + 0):2 = 0,33593   0,01010112 = 0,33593 ≈ 0,33610
Десятичное в восьмеричное	1∙8 + 5 = 13 13∙8 + 4 = 108   1548 = 10810	5:8 = 0,625 (0,625 + 0):8 = 0,078125 (0,078125 + 6):8 = 0,75976 (0,75976 + 5):8 = 0,71997 (0,71997 + 2):8 = 0,33999   0,256058 = 0,33999 ≈ 0,34010
Десятичное в шестнадцатеричное	6∙16 + 12 = 108   6С16 = 10810	A:16 = 0,625 (0,625 + 0):16 = 0,039062 (0,039062 + 6):16 = 0,75976 (0,75976 + 7):16 = 0,71997 (0,71997 + 5):16 = 0,33999   0,570A16 = 0,33999 ≈ 0,34010

Таблица 1.3.2 – Методы перевода целых и дробных чисел из десятичной СС

Тип преобразования	Целые числа	Дробные числа
Деление данного десятичного числа на q. Остатки дают превращенное число, которое читается в обратном направлении	Повторное умножение данного десятичного числа на q. Разряд перед запятой дает разряд превращенного числа. При дальнейшем умножении используется лишь дробная часть промежуточного результата
Десятичное в двоичное	108:2 = 54 остаток 0 54:2 = 27 остаток 0 27:2 = 13 остаток 1 13:2 = 6 остаток 1 6:2 = 3 остаток 0 3:2 = 1 остаток 1 1:2 = 0 остаток 1   10810 = 11011002	0,34∙2 = 0,68 переносится 0 0,68∙2 = 1,36 переносится 1 0,36∙2 = 0,72 переносится 0 0,72∙2 = 1,44 переносится 1 0,44∙2 = 0,88 переносится 0 0,88∙2 = 1,76 переносится 1 0,76∙2 = 1,52 переносится 1   Прерывание 0,3410 = 0,01010112
Десятичное в восьмеричное	108:8 = 13 остаток 4 13:8 = 1 остаток 5 1:8 = 0 остаток 1   10810 = 1548	0,34∙8 = 2,72 переносится 2 0,72∙8 = 5,76 переносится 5 0,76∙8 = 6,08 переносится 6 0,08∙8 = 0,64 переносится 0 0,64∙8 = 5,12 переносится 5   Прерывание 0,3410 = 0,256058
Десятичное в шестнадцатеричное	108:16 = 6 остаток 12 6:16 = 0 остаток 6   10810 = 6С16	0,34∙16 = 5,44 переносится 5 0,44∙16 = 7,04 переносится 7 0,04∙16 = 0,64 переносится 0 0,64∙16 = 10,24 переносится 10   Прерывание 0,3410 = 0,570A8

Для перевода чисел из одной СС в другую удобно использовать промежуточное преобразование числа в двоичную СС.

Таблица 1.3.3 – Методы перевода целых чисел из одной СС в другую СС

Десятичное число	Двоичное число	Восьмеричное число	Десятичное число	Двоичное число	Шестнадцатеричное число
					A
					B
					C
					D
					E
					F

Перевод [восьмеричное число] ↔ [двоичное число]
24518 = 010.100.101.001 = 101001010012
Восьмеричные цифры
Двоичные триады
1010011110102 = 101.001.111.010 = 51728
Двоичные триады
Восьмеричные цифры

Перевод [шестнадцатеричное число] ↔ [двоичное число]
4C716 = 0100.1100.0111 = 100110001112
Шестнадцатеричные цифры		С
Двоичные тетрады
1010001111102 = 1010.0011.1110 = A3E16
Двоичные тетрады
Шестнадцатеричные цифры	A		E

Перевод [восьмеричное число] → [двоичное число] → [шестнадцатеричное число]
24518 = 010.100.101.001 = 101001010012
Восьмеричные цифры
Двоичные триады
101001010012 = 0101.0010.1001 = 52916
Двоичные тетрады
Шестнадцатеричные цифры
24518 = 010.100.101.001 = 101001010012 = 0101.0010.1001 = 52916
Перевод [шестнадцатеричное число] → [двоичное число] → [восьмеричное число]
4C716 = 0100.1100.0111 = 100110001112
Шестнадцатеричные цифры		С
Двоичные тетрады
100110001112 = 010.011.000.111 = 23078
Двоичные триады
Восьмеричные цифры
4C716 = 0100.1100.0111 = 100110001112 = 010.011.000.111 = 23078

Двоичная арифметика

Арифметические действия над двоичными числами выполняются следующим образом:

Сложение	Вычитание	Умножение
0 + 0 = 0	0 – 0 = 0	0∙0 = 0
0 + 1 = 1	1 – 0 = 1	0∙1 = 0
1 + 0 = 1	1 – 1 = 0	1∙0 = 0
1 + 1 = 10	10 – 1 = 1	1∙1 = 1

Сложение двух многоразрядных двоичных чисел проводится поразрядно с учетом единиц переполнения от предшествующих разрядов:

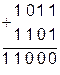
Вычитание многоразрядных двоичных чисел, аналогично сложению, начинается из младших разрядов. Если занять единицу в старшем разряде, образуются две единицы в младшем разряде:

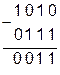
Умножение представляет собой многоразовое сложение промежуточных сумм и сдвиги:

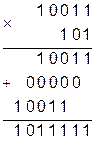
Процесс деления состоит из операций вычитания, которые повторяются: