Лабораторная работа №3. Организация вычислительного эксперимента и оценка его результатов средствами программного средства ARENA

Откройте модель, разработанную в лабораторной работе №2 (рис.2.2).

Организация вычислительного эксперимента включает:

• выбор способов (методов) учета случайности внутри системы и для вероятностных входных данных;

• определение длительности переходного процесса моделирования;

• определение длительности одного прогона;

• определение количества прогонов (реализаций) модели;

• выбор способа сбора данных для каждого прогона;

• выбор методов оценки точности выходных данных с построением доверительных интервалов;

• описание условий эксперимента и возможных сценариев.

Выбор способов (методов) учета случайности внутри системы и для вероятностных входных данных

При выполнении лабораторной работы №2 все параметры, касающиеся случайных величин, были определены. Проверьте их по рис.2.3.

Определение длительности переходного процесса моделирования

Используя пункт меню Run/Setup, установите неопределенную длительность реализации.

Пусть, например, нас, прежде всего, интересует время, которое тратится на ожидание герметизации. Постройте график с параметрами, показанными на рис.3.1.

Рис. 3.1. Время в очереди Sealer Process.Queue

Запустите модель и проследите, когда среднее время ожидания герметизации начнет колебаться около установившегося значения (рис.3.2).

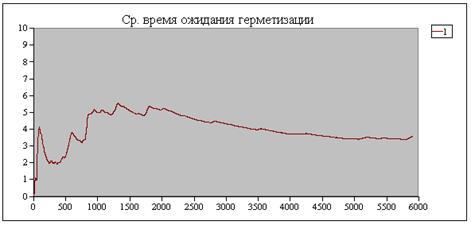
Рис. 3.2. Определение длительности переходного процесса моделирования

Из рис.3.2 видно, что длительности переходного процесса составляет примерно 4000 мин (рис.3.3).

Определение длительности одного прогона

Используя пункт меню Run/Setup, задайте длительность, как показано на рис.3.3.

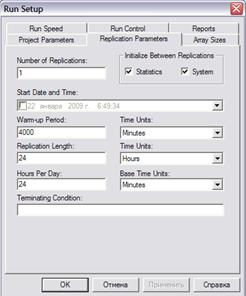
Рис. 3.3. Задание длительности реализации

Определение количества прогонов (реализаций) модели

Для обеспечения требуемой точности результатов количество реализаций модели определяется из выражения:

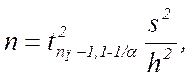
где t – статистика Стьюдента, определяемая таблично;

n_П – число предварительных прогонов модели (30 …40);

a - уровень значимости;

s - выборочное стандартное отклонение для предварительного набора повторений;

h – требуемая полуширина доверительного интервала оцениваемого параметра.

Используя пункт меню Run/Setup, задайте число предварительных прогонов модели равное 30 и включите режим без анимации (Run/Run Control/Butch Run).

По окончании имитации посмотрите отчет (рис.3.4).

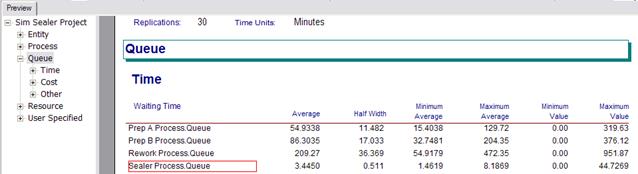
Рис. 3.4. Временные характеристики очереди

Для уровня значимости 5% (a=0,05) t=1,96.

Из рис.48 h=0,511 (пусть она останется требуемой), s»22.

Подставив эти данные в выражение для расчета n, получим требуемое число реализаций »7047.