Статистические велечины. основные понятия математической статистики

ВВЕДЕНИЕ

Общая теория измерений — это формально-логические основания измерения как процесса познания.

В данных методических указаниях приводятся сведения по организации и порядку проведения работ по математическим методам обработки результатов измерений, математическим моделям измеряемых величин, погрешностям измерений и способами их выявлений.

СТАТИСТИЧЕСКИЕ ВЕЛЕЧИНЫ. ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

Теория случайных погрешностей использует математический аппарат теории вероятностей и математической статистики и основывается на рассмотрении появления случайных погрешностей при многократно повторяемых наблюдениях как случайных событий. Теория вероятностей есть математическая наука, изучающая закономерности в случайных явлениях.

Под случайным явлением понимают такое явление, которое при многократном повторении одного и того же опыта протекает каждый раз иначе. Примером может служить стрельба из орудия, установленного под заданным углом к горизонту. Фактическая траектория полета каждого отдельного снаряда отличается от теоретической из-за влияния многих факторов: ошибки в изготовлении снаряда, разной массы заряда, изменения метеорологических условий на трассе во время полета снаряда и т.д.

Событием называют все то, о чем в результате опыта можно сказать «произошло», «не произошло» или «появилось», «не появилось». Например, отказ прибора является событием. Событие называется достоверным, если оно обязательно происходит в результате опыта, т.е. не может не произойти; событие называется невозможным, если оно не может произойти в результате данного опыта. Событие, которое может произойти или не произойти в результате опыта, называется случайным.

Вероятность события - это численная мера степени объективной возможности этого события.. Практический смысл этого понятия заключается в том, что на основании опыта считают более вероятными те события, которые происходят чаще; менее вероятными - те события, которые происходят реже; маловероятными - те, которые почти никогда не происходят. Следовательно, понятие вероятности события связано с понятием частоты события.

Под частотой события понимается отношение числа опытов, в которых данное событие произошло, к числу всех произведенных опытов. Частота достоверного события всегда равна единице, а частота невозможного события всегда равна нулю. Частота случайного события представляет собой правильную дробь, но может быть также равна нулю или единице. Если событие ни разу не произошло в опытах, его частота равна нулю.

Случайной величиной называют такую величину, которая принимает в результате опыта одно из множества возможных значений, причем заранее неизвестно, какое именно. Например, число приборов, отказывающих в течение данного интервала времени при эксплуатации, является случайной величиной. Возможными значениям этой случайной величины являются целые числа 0, 1, 2, ..., п.

Случайные величины бывают двух типов - прерывные (дискретные) и непрерывные.

Прерывные (дискретные) случайные величины - это случайные величины, возможные значения которых распределены дискретно по числовой оси.

Непрерывные случайные величины - это случайные величины,
возможные значения которых распределены непрерывно по числовой оси или некоторой ее части. Например, частота появления события N при п опытах
вляется прерывной случайной величиной, а время безотказной работы прибора - непрерывной случайной величиной.

Имеется прерывная случайная величина X. Через х_и х₂, ..., х_п обозначим возможные значения этой случайной величины, а через P_i, Р₂, …, Р_n - вероятности событий, заключающихся в том, что величина X принимает значения x_i, х_г, ..., х_п соответственно. Причем случайная величина X в каждом опыте может принять только одно из возможных значений х, т. е. в каждом опыте реализуется одно из следующих событий: X = x_i, X = х₂, ..., X = х_п.

Если события образуют полную группу несовместных событий, то сумма их вероятностей равна единице.

Лабораторная работа №1

Определение величины технологического допуска статистическим
методом

Цель работы

По результатам измерения партии одинаковых деталей рассчитать технологический допуск на заданный номинальный размер и назначить стандартное поле допуска. Построить гистограмму фактического распределения размеров по размерным группам.

Теоретические предпосылки

В теории ошибок принято точность измерений (точность прибора) характеризовать с помощью среднего квадратического отклонения σ случайных ошибок измерений. Для оценки σ используют «исправленное» среднее квадратическое отклонение s. Поскольку обычно результаты измерений взаимно независимы, имеют одно и то же математическое ожидание (истинное значение измеряемой величины) и одинаковую дисперсию (в случае равноточных измерений)

Основными характеристиками рассеяния случайных ошибок являются среднее арифметическое значение действительных размеров М и среднеквадратичное отклонение σ , которые находят по формулам:

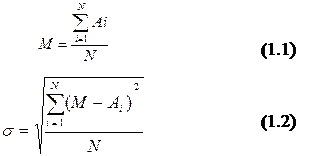где А_i- действительные размеры, полученные в результате намерений;

N- количество деталей (объем выборки).

Для наглядного графического представления о рассеянии размеров строят гистограмму распределения деталей по размерным группам. С этой целью весь диапазон размеров данной выборки от минимального A_min до максимального A_max разбивают на К групп.

Размеры, входящие в одну группу, могут отличаться друг от друга на величину, не превышающую значения :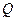

Технологический расчетный допуск ТR находят по формуле:

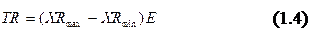где XR_max, XR_min- соответственно максимальный и минимальный расчетные размеры, учитывающие только случайные ошибки и определяемые из выражений:

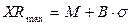, (1.5)

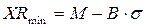(1.6)

Значения коэффициента Bприведены для соответствующих объемов выборки в вариантах задач. Они гарантирует, что 99,73% деталей генеральной совокупности будут иметь размеры в пределах назначенного допуска. Коэффициент Е в формуле (1.4) дает поправку на систематические погрешности. Для налаженных технологических процессов он составляет 1,05-1,2.

При назначении стандартных предельных отклонений отверстий следует отыскать в ГОСТ 25347-82 для данного номинального размера нижнее отклонение, наиболее близкое к XR_min, и верхнее отклонение, наиболее близкое к (ХR_min + ТR). Для размеров валов наоборот: верхнее отклонение должно соответствовать XR_max, а нижнее - (XR_max-ТR). Этот прием обоснован тем, что при настройке станка центр группирования размеров M несколько сдвигается в минус для отверстий и в плюс для валов, что уменьшает риск появления неисправимого брака и позволяет увеличить время работы инструмента до следующей перенастройки или заточки.