Практика 2.2. О необходимости уточнения понятия алгоритма. Машина Тьюринга

Вопросы и задания для подготовки к занятию:

1. Любые ли задачи имеют решение (можно указать алгоритм решения)? Приведите по 3 примера задач (из истории развития математики), которые имеют решение (алгоритм известен) и не имеют решения (алгоритм решения не был найден).

2. Для задач, которые имеют решение, укажите «начальные данные» и искомый результат.

3. Что такое алгоритмический процесс?

4. В связи с чем возникла необходимость уточнения понятия алгоритма?

5. С именами каких математиков (не менее 6 человек) связано уточнение понятие алгоритма (указать полные имена и фамилии, годы жизни, страну)? [1, с.317]

Вопросы для обсуждения:

1. Определение машины Тьюринга.

Во-первых, посмотрите видеоурок [2], выпишите главные моменты (можно сделать скриншоты экрана), во-вторых, изучите материал по учебнику [1, с. 317-319].

a) Какова природа машины Тьюринга? Что она из себя представляет?

b) Кем, когда в связи с чем было сформулировано понятие «машина Тьюринга»?

c) Основные элементы машины Тьюринга и их характеристика: лента и её алфавит символов (внешний), устройство управления и алфавит движений, считывающая головка и её алфавит внутренних состояний. Как изображается каждый из элементов машины Тьюринга?

d) Каким образом устроена программа (функциональная схема), определяющая работу машины? Какие существуют способы записи программы?

e) Как работает машина Тьюринга?

f) Что называют словом в машине Тьюринга?

g) Что такое конфигурация машины и какая конфигурация называется заключительной?

h) Что означает «слово А перерабатывается машиной в слово В»?

2. Применение машины Тьюринга к словам[1, с. 320-322],[3].

Проиллюстрируйтё все введенные понятия на примерах. Нужно научиться воспроизводить ход рассуждений самостоятельно.

Литература:

1. Игошин В.И. Математическая логика и теория алгоритмов. Москва, Академия, 2008. – 448 с.

2. Машины Тьюринга. Урок 1. Turing Machines. Lesson 1 https://www.youtube.com/watch?v=8jAu5Ts0oFg

3. Машины Тьюринга. Урок 2. Turing Machines. Lesson 2 https://www.youtube.com/watch?v=OPr_Ks4lvy0

ПРИЛОЖЕНИЕ

«Парадоксы, обнаруженные в основаниях математики в начале XX века, вызвали к жизни различные концепции и течения, призванные эти парадоксы устранить»

Парадоксы (логики и теории множеств) — (греч. 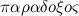— неожиданный) — формально-логические противоречия, которые возникают в содержательной множеств теории и формальной логике при сохранении логической правильности рассуждения. Парадоксы возникают тогда, когда два взаимоисключающих (противоречащих) суждения оказываются в равной мере доказуемыми. Парадоксы могут появиться как в пределах научной теории, так и в обычных рассуждениях (например, приводимая Расселом перифраза его парадокса о множестве всех нормальных множеств: «Деревенский парикмахер бреет всех тех и только тех жителей своей деревни, которые не бреются сами. Должен ли он брить самого себя?»). Поскольку формально-логическое противоречие разрушает рассуждение как средство обнаружения и доказательства истины (в теории, в которой появляется парадокс, доказуемо любое, как истинное, так и ложное, предложение), возникает задача выявления источников подобных противоречий и нахождения способов их устранения. Проблема философского осмысления конкретных решений парадоксов — одна из важных методологических проблем формальной логики и логических оснований математики.

Парадокс Берри

Внешне простой парадокс был указан в самом начале нашего века Д. Берри, занимавшем должность библиотекаря Оксфордского университета. Позже он был опубликован Бертраном Расселом.

В русской интерпретации он звучит так:
Множество натуральных чисел бесконечно. Множество же тех имен этих чисел, которые имеются в русском языке и содержат меньше, чем, допустим, сто слов, является конечным.
Это означает, что существуют такие натуральные числа, для которых в русском языке нет имен менее чем из ста слов. Среди этих чисел есть, очевидно, наименьшее число. Его нельзя назвать посредством русского выражения, содержащего менее ста слов. Но выражение «наименьшее натуральное число, для которого не существует в русском языке его сложное имя, слагающееся из менее чем ста слов» является как раз именем этого числа. Это имя сформулировано в русском языке и содержит только девятнадцать слов. Очевидный парадокс: названным оказалось то число, для которого нет имени.

Парадокс Маннури (О мэре)

Похожим на парадокс «О парикмахере» является парадокс "О мэре" голландского математика Геррита Маннури (1867-1956).

В этом парадоксе речь идет о стране, состоящей из отдельных областей. Каждая из которых имеет мэра, который, однако, не обязательно должен жить в той же области, которой он управляет. На основании этой оговорки всех мэров можно разделить на две категории. К одной из них относятся те мэры, которые живут в той же области, которой они управляют, — их мы назовем «хорошими»; к другой относятся все те, которые не живут в той области, которой они управляют, — этих мы назовем «плохими». Известно также, что президент страны выделил для плохих мэров отдельную область и издал приказ, обязывающий всех плохих мэров переселиться именно в эту новую область.

Кроме того в приказе было сказано, что в новой области никто кроме плохих мэров проживать не может. Очевидно, новая область должна была иметь и своего мэра.
В связи с этим спрашивается: каким будет этот мэр — хорошим или плохим? Если он хороший, то он должен жить в той области, которой он управляет, но там он жить не может, так как эта область создана только для плохих мэров, а он, по предположению, хороший. Если же он плохой, то с одной стороны из определения понятия «плохой» следует, что он не должен жить в той области, которой он управляет, а с другой стороны он должен жить именно в этой области, так как она специально создана для плохих мэров. Таким образом, возникает та же самая неразрешимая ситуация: мэр особой области не может быть ни хорошим, ни плохим; и не может жить ни в самой этой области, ни вне ее.

В чем же дело? Причина парадокса в том, что иерархические уровни опять оказались спутанными. В данном случае все жители рассматриваемого государства распадаются на три категории: обыкновенные граждане, мэры обычных областей, и мэр той особой области, в которой живут все плохие мэры. Мэр особой области существенно отличается от остальных мэров: обычные мэры управляют гражданами, а мэр особой области управляет мэрами — это новый, более высокий иерархический уровень. Свойства «быть плохим мэром» и «быть хорошим мэром» пригодны только для характеристики обычных мэров, а мэр особой области относится к другой категории, — его характеризуют другие свойства, и поэтому бессмысленно спрашивать, хороший он, или плохой.

Выявленное противоречие как раз и показывает, что он не может быть ни тем, ни другим. Принципиальное различие в свойствах элементов различных иерархических уровней на практике обычно сразу же бросается в глаза. Например, все яблоки, лежащие на столе, могут быть желтыми — это их общее свойство. Но множество этих яблок желтым быть не может, так как множество яблок — это абстрактный, идеальный предмет, относящийся к совершенно другому иерархическому уровню. Элементы определенного иерархического уровня либо обладают некоторым, естественным для них свойством, либо нет. Ничего другого быть не может. Третьего не дано.

Поэтому, когда обнаруживается элемент, который не может обладать; этим свойством и в то же время не может не обладать им, а третьего не дано, то это противоречие кажется неразрешимым. Но это только кажущееся противоречие. Третье все же дано! Рассматриваемый элемент на самом деле относится к другой категории и обладает другими свойствами. Свойства элементов различных иерархических уровней совершенно различны— они не сводимы друг к другу. Свойства элементов более высокого уровня нельзя определить, нельзя объяснить, нельзя свести к свойствам элементов какого-либо другого уровня.

Таким образом, можно сказать, что рассмотренные парадоксы возникают вследствие игнорирования иерархических различий. Следует заметить, что в каждом из рассмотренных парадоксов имеется неосознанное и к тому же неправомерное предположение. Именно оно и приводит к противоречию. Поэтому парадокс на самом деле следует рассматривать как доказательство ошибочности принятого предположения. Здесь, по существу, имеет место доказательство "от противного". В основном все эти парадоксы семантический характер. Язык играет существенную роль. Возникновение странных петель и обнаружение иерархических различий так или иначе всегда связано с языком. Но кроме естественного языка, используемого при речевом общении, существуют и другие языки: язык изобразительного искусства и язык музыки. В этих языках тоже есть различные иерархические уровни. Поэтому и здесь спутанность иерархий по необходимости приводит к возможности образования странных, парадоксальных петель. Но сконструировать такую петлю — дело не легкое, оно требует большой изобретательности и большого мастерства.