Z1 Ù z2 Ú z3 Ù z4 Ù z5 1 страница

Про обозначения

К сожалению, обозначения логических операций И, ИЛИ и НЕ, принятые в «серьезной» математической логике (Ù,Ú,), неудобны, интуитивно непонятны и никак не проявляют аналогии с обычной алгеброй. Автор, к своему стыду, до сих пор иногда путает Ù и Ú. Поэтому на его уроках операция «НЕ» обозначается чертой сверху, «И» – знаком умножения (поскольку это все же логическое умножение), а «ИЛИ» – знаком «+» (логическое сложение).
В разных учебниках используют разные обозначения. К счастью, в начале задания ЕГЭ приводится расшифровка закорючек (Ù,Ú,), что еще раз подчеркивает проблему.

Что нужно знать:

· условные обозначения логических операций

A, 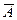не A (отрицание, инверсия)

A Ù B, 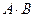A и B (логическое умножение, конъюнкция)

A Ú B, 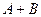A или B (логическое сложение, дизъюнкция)

A→B импликация (следование)

AºB эквивалентность (равносильность)

· операцию «импликация» можно выразить через «ИЛИ» и «НЕ»:

A→B = A Ú Bили в других обозначениях A→B =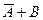

· иногда для упрощения выражений полезны формулы де Моргана:

(A Ù B) = A Ú B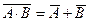

(A Ú B) = A Ù B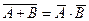

· если в выражении нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ», «импликация», и самая последняя – «эквивалентность»

· таблица истинности выражения определяет его значения при всех возможных комбинациях исходных данных

· если известна только часть таблицы истинности, соответствующее логическое выражение однозначно определить нельзя, поскольку частичной таблице могут соответствовать несколько разных логических выражений (не совпадающих для других вариантов входных данных);

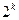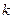· количество разных логических выражений, удовлетворяющих неполной таблице истинности, равно , где – число отсутствующих строк; например, полная таблица истинности выражения с тремя переменными содержит 2³=8 строчек, если заданы только 6 из них, то можно найти 2^8-6=2²=4 разных логических выражения, удовлетворяющие этим 6 строчкам (но отличающиеся в двух оставшихся)

· логическая сумма A + B + C + … равна 0 (выражение ложно) тогда и только тогда, когда все слагаемые одновременно равны нулю, а в остальных случаях равна 1 (выражение истинно)

· логическое произведение A · B · C · … равно 1 (выражение истинно) тогда и только тогда, когда все сомножители одновременно равны единице, а в остальных случаях равно 0 (выражение ложно)

· логическое следование (импликация) А→В равна 0 тогда и только тогда, когда A (посылка) истинна, а B (следствие) ложно

· эквивалентность АºB равна 1 тогда и только тогда, когда оба значения одновременно равны 0 или одновременно равны 1

Пример задания (М.В. Кузнецова):

Р-15. Логическая функция F задаётся выражением (x Ú y Ú z) Ù (x Ú y). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z?

	?	?	?	F

В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая 1-му столбцу; затем – буква, соответствующая 2-му столбцу; затем – буква, соответствующая 3-му столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Решение (М.В. Кузнецова, через СКНФ и сопоставление таблиц истинности):

1) Запишем заданное выражение в более простых обозначениях:

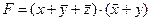
2) Функция 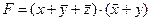задана в виде КНФ (конъюнктивной нормальной формы), которую можно привести к СКНФ, используя известные тождества алгебры логики: 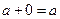, 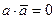и распределительный закон для операции «И» .

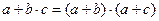Вторую дизъюнкцию дополним недостающей переменной z:

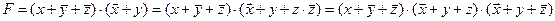
СКНФ:

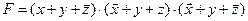
3) Каждая дизъюнкция в СКНФ соответствует строке таблицы истинности, в которой F=0. Используя полученную СДНФ, делаем вывод: в таблице истинности имеется 3 строки, где F=0, заполним их:

	x	y	z	F

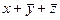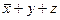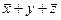4) В таблице, приведенной в задании, рассмотрим строки, где F=0:

?	?	?	F

5) Сравнивая столбцы этих таблиц, делаем выводы:

a. во втором (синем) столбце таблицы задания находится y (одна единица),

b. в первом (жёлтом) столбце таблицы задания находится z (в двух строках z=y),

c. в последнем (зелёном) столбце таблицы задания находится x (где z=y, там x=y).

6) Ответ: zyx.

Решение (Л.Л. Воловикова, через уравнение):

1) Так как между скобками стоит операция И, решим уравнение:

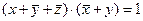
2) Чтобы функция была равна 1, нужно чтобы каждая скобка была равна 1.

3) Уравнение 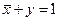имеет 3 решения:

x	y

4) Подставим найденные решения в первую скобку и найдем полный набор решений уравнения:

	x	y	z	F

5) Сопоставляем найденное решение со строками исходной таблицы, в которых функция F=1:

	?	?	?	F

6) Есть одна строка, где две переменных равна 1, а одна – нулю, это строка 3 в последней таблице и строка 4 в предпоследней, поэтому первый столбец соответствует z

7) Далее видим, что в столбце у в предпоследней таблице три единицы, а в последней таблице три единицы только во втором столбце, поэтому второй столбец – y, а третий – x.

8) Ответ: zyx.

Ещё пример задания:

Р-14. Логическая функция F задаётся выражением (z)Ù x Ú x Ù y. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z?

?	?	?	F

В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая 1-му столбцу; затем – буква, соответствующая 2-му столбцу; затем – буква, соответствующая 3-му столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Решение (через полную таблицу):

9) запишем заданное выражение в более простых обозначениях:

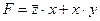
10) общий ход действий можно описать так: подставляем в эту формулу какое-нибудь значение (0 или 1) одной из переменных, и пытаемся определить, в каком столбце записана эта переменная;

11) например, подставим x = 0, при этом сразу получаем F = 0; видим, что переменная x не может быть ни в первом, ни во втором столбце (противоречие во 2-й строке):

?	?	?	F

а в третьем – может:

?	?	x	F

12) подставим x = 1, тогда 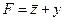; логическая сумма равна 0 тогда и только тогда, когда все слагаемые равны 0, это значит, что 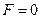только в одном случае – при z = 1 и y = 0;

13) ищем такую строчку, где x = 1 и :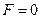

?	?	x	F

14) как мы видели, в этой строке таблицы должно быть обязательно z = 1 и y = 0; поэтому z – в первом столбце, а y – во втором

15) Ответ: zyx.

Решение (преобразование логического выражения, Дегтярева Е.В.):

1) Используя законы алгебры логики, а именно распределительный для операции «ИЛИ» (см. учебник 10 кл. 1 часть, стр. 185), запишем заданное выражение:

;

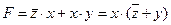2) Поскольку добиться логической единицы в произведении сложнее, чем в сумме рассмотрим строки таблицы, где произведение равно 1(это 2-я, 4-я и 8-я строки );

3) Во 2-й строке Х обязательно должно быть равно 1. Поэтому Х может быть только в третьем столбце, в первых двух могут быть и Y, и Z.

?	?	х	F

4) Анализируя 4 строку приходим к выводу, что в первом столбце таблицы может быть только Z, во втором – Y.

z	y	х	F

5) В 8-й строке убеждаемся в верности своих рассуждений:

z	y	х	F

Т.о., немного упростив выражение, уменьшили количество рассматриваемых строк.

6) Ответ: zyx.

Решение (преобразование логического выражения, СДНФ, В.Н. Воронков):

1) Рассмотрим строки таблицы, где функция равна 1

a	b	c	F

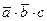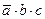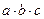и построим логическое выражение для заданной функции, обозначив переменные через a, b и с (см. § 22 из учебника для 10 класса):

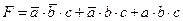
2) Упрощаем это выражение, используя законы алгебры логики:

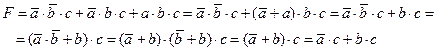
3) Сравнивая полученное выражение с заданным 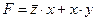, находим, что a = z, b = y и c = x.

4) Ответ: zyx.

Решение (сопоставление таблиц истинности, М.С. Коротков):

1) Рассмотрим строки таблицы, где функция равна 1, обозначив переменные через a, b и с

a	b	c	F

и сопоставим эти строки с теми строками таблицы истинности заданной функции 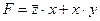, где F = 1:

x	y	z	F

2) Сравнивая столбцы интересующих нас строк, определяем, что c = x (все три единицы в зеленых ячейках), b = y (один ноль и две единицы) и a = z (два ноля и единица).

3) Ответ: zyx.

Решение (М.В. Кузнецова, через приведение к СДНФ):

1) Функция 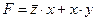задана в виде ДНФ (дизъюнктивной нормальной формы), которую не сложно привести к СДНФ, используя известные тождества алгебры логики:
a ∙ 1 = a и .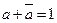

Каждую конъюнкцию дополним недостающей переменной:

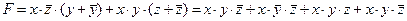
СДНФ:

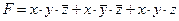
2) Каждая конъюнкция в СДНФ соответствует строке таблицы истинности, в которой F=1. Используя полученную СДНФ, делаем вывод: в таблице истинности имеется 3 строки, где F=1, заполним их:

	x	y	z	F

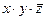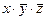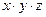3) В таблице, приведенной в задании, рассмотрим строки, где F=1:

?	?	?	F

4) Сравнивая столбцы этих таблиц, делаем выводы:

a. в первом (жёлтом) столбце таблицы задания находится z (одна единица),

b. во втором (синем) столбце таблицы задания находится y (две единицы),

c. в последнем (зелёном) столбце таблицы задания находится x (все единицы).

5) Ответ: zyx.

Ещё пример задания:

Р-13. Каждое логическое выражение A и B зависит от одного и того же набора из 5 переменных. В таблицах истинности каждого из этих выражений в столбце значений стоит ровно по 4 единицы. Каково минимально возможное число единиц в столбце значений таблицы истинности выражения A Ú ØB?

Решение:

1) полная таблица истинности каждого выражения с пятью переменными содержит 2⁵ = 32 строки

2) в каждой таблице по 4 единицы и по 28 (= 32 – 4) нуля

3) выражение A Ú ØB равно нулю тогда и только тогда, когда A = 0 и B = 1

4) минимальное количество единиц в таблице истинности выражения A Ú ØB будет тогда, когда там будет наибольшее число нулей, то есть в наибольшем количество строк одновременно A = 0 и B = 1

5) по условию A = 0 в 28 строках, и B = 1 в 4 строках, поэтому выражение A Ú ØB может быть равно нулю не более чем в 4 строках, оставшиеся 32 – 4 = 28 могут быть равны 1

6) Ответ: 28.

Ещё пример задания:

Р-12. Дан фрагмент таблицы истинности для выражения F:

x1	x2	x3	x4	x5	F

Укажите максимально возможное число различных строк полной таблицы истинности этого выражения, в которых значение x1 не совпадает с F.

Решение:

1) полная таблица истинности выражения с пятью переменными содержит 2⁵ = 32 строки

2) в приведённой части таблицы в двух строках значение x1 совпадает с F, а в одной – не совпадает

3) во всех оставшихся (неизвестных) 32 – 3 = 29 строках значения x1 и F могут не совпадать

4) всего несовпадающих строк может быть 1 + 29 = 30.

5) Ответ: 30.

Ещё пример задания:

Р-11. Александра заполняла таблицу истинности для выражения F. Она успела заполнить лишь небольшой фрагмент таблицы:

x1	x2	x3	x4	x5	x6	x7	x8	F

Каким выражением может быть F?

1) x1 Ù x2 Ù x3 Ù x4 Ù x5 Ù x6 Ù x7 Ù x8

2) x1 Ú x2 Ú x3 Ú x4 Ú x5 Ú x6 Ú x7 Ú x8

3) x1 Ù x2 Ù x3 Ù x4 Ù x5 Ù x6 Ù x7 Ù x8

4) x1 Ú x2 Ú x3 Ú x4 Ú x5 Ú x6 Ú x7 Ú x8

Решение:

1) перепишем выражения в более простой форме, заменив «И» (Ù) на умножение и «ИЛИ» (Ú) на сложение:

1)

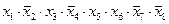
2)

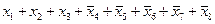
3)

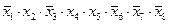
4)

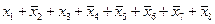
2) в последнем столбце таблицы истинности видим две единицы, откуда сразу следует, что это не может быть цепочка операций «И» (конъюнкций), которая даёт только одну единицу; поэтому ответы 1 и 3 заведомо неверные

3) анализируем первую строку таблицы истинности; мы знаем в ней только два значения - и

4) для того, чтобы в результате в первой строке получить 0, необходимо, чтобы переменная 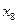входила в сумму с инверсией (тогда из 1 получится 0!), это условие выполняется для обоих оставшихся вариантов, 2 и 4

5) кроме того, переменная 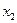должна входить в выражение без инверсии (иначе соответствующее слагаемое в первой строке равно 1, и это даст в результате 1); этому условию не удовлетворяет выражение 4; остается один возможный вариант – выражение 2

6) Ответ: 2.

Ещё пример задания:

Р-10. Александра заполняла таблицу истинности для выражения F. Она успела заполнить лишь небольшой фрагмент таблицы:

x1	x2	x3	x4	x5	x6	x7	x8	F

Каким выражением может быть F?

1) x1 Ù x2 Ù x3 Ù x4 Ù x5 Ù x6 Ù x7 Ù x8

2) x1 Ú x2 Ú x3 Ú x4 Ú x5 Ú x6 Ú x7 Ú x8

3) x1 Ù x2 Ù x3 Ù x4 Ù x5 Ù x6 Ù x7 Ù x8

4) x1 Ú x2 Ú x3 Ú x4 Ú x5 Ú x6 Ú x7 Ú x8

1) перепишем выражения в более простой форме, заменив «И» (Ù) на умножение и «ИЛИ» (Ú) на сложение:

1)

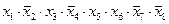
2)

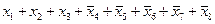
3)

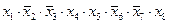
4)

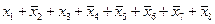
2) в последнем столбце в таблице видим одну единицу и два нуля, поэтому это не может быть дизъюнкция, которая даёт ноль только при одном наборе значений переменных; таким образом, варианты 2 и 4 заведомо неверные, нужно сделать выбор между ответами 1 и 3

3) рассматриваем «особую» строчку таблице, в которой функция равна 1;

4) поскольку мы говорим о конъюнкции, переменная 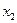должна входить в неё с инверсией (это выполняется для обоих оставшихся вариантов), а переменная 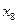– без инверсии; последнее из этих двух условий верно только для варианта 3, это и есть правильный ответ.

5) Ответ: 3.

Ещё пример задания:

Р-09. Александра заполняла таблицу истинности для выражения F. Она успела заполнить лишь небольшой фрагмент таблицы:

x1	x2	x3	x4	x5	x6	x7	x8	F

Каким выражением может быть F?