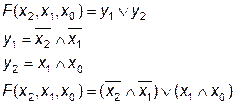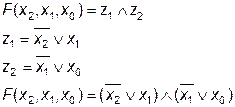Тема 1.6 Логические основы ЭВМ
Минимизация булевых функций
Логическую схему, которая реализует заданный алгоритм преобразования сигналов, можно синтезировать непосредственно по выражению, представленному в виде СДНФ или СКНФ. Однако полученная при этом схема не оптимальна с точки зрения ее практической реализации. Поэтому исходную логическую функцию необходимо минимизировать. Целью минимизации логической функции является уменьшение стоимости ее технической реализации.
Основные требования к задаче синтеза логической схемы: минимальное число элементарных конъюнкций или дизъюнкций в логическом выражении и однородность используемых операций. Кроме того, могут существовать ограничения по выбору элементной базы для синтезируемого устройства.
Метод непосредственных преобразований
Метод основан на применении к СНДФ и СКНФ логической функции законов алгебры логики.
Пример:
Минимизировать ФАЛ 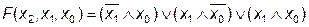 .
.
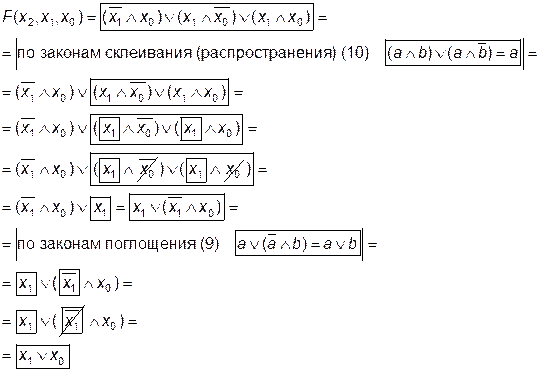
Пример для вышерассмотренной таблицы истинности:
| x2 | x1 | x0 | y = f(x2,x1,x0) | СДНФ | СКНФ |
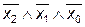 | – | ||||
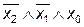 | – | ||||
| – | 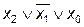 | ||||
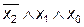 | – | ||||
| – | 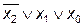 | ||||
| – | 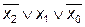 | ||||
| – | 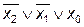 | ||||
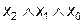 | – |
Минимизация СДНФ (самостоятельно):
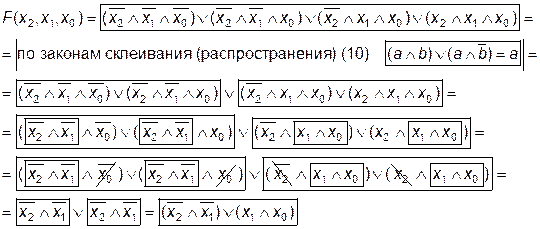
Минимизация СКНФ (самостоятельно):
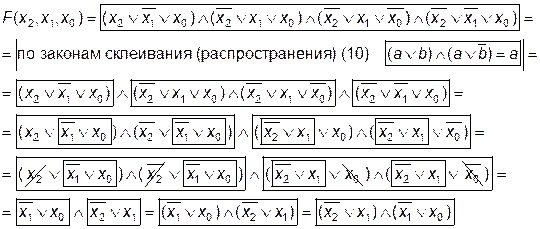
Функции 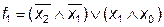 и
и 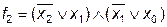 равнозначны.
равнозначны.
Метод Карно-Вейча
Метод диаграмм Вейча, усовершенствованный Карно, применяется в случае, если число аргументов ФАЛ не больше 5–6. Карты Карно – это графическое представление таблиц истинности. Каждой комбинации переменных ставится в соответствие клетка карты Карно. В клетку записывается значение ФАЛ (0 или 1) для данной комбинации входных переменных. Входные переменный располагаются по внешним сторонам карты напротив ее строк и столбцов.
Пример:
Для вышерассмотренной таблицы истинности:
| x2 | x1 | x0 | y = f(x2,x1,x0) |
Карта Карно для ФАЛ трех переменных по приведенной таблице истинности имеет вид:
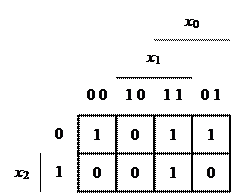 |
Каждая из входных переменных делит по-своему любую карту Карно на две равные части, в одной из которых значение этой переменной равняется «1», а в другой – «0». Каждой клетке карты отвечает определенная комбинация значений всех входных переменных, а каждая сторона клетки представляет собой границу между значениями переменных. Число клеток карты Карно определяется величиной 2n, где n – число входных переменных ФАЛ.
Свойства карты Карно:
· комбинации значений переменных для соседних клеток карты Карно различаются значением только одной входной переменной. При переходе с одной клетки в соседнюю клетку всегда изменяется значение только одной переменной на ее инверсное значение;
· соседними являются между собой крайние левые и крайние правые клетки карты, а также крайние верхние и крайние нижние клетки (как если бы карты были свернуты в цилиндры по вертикали и горизонтали).
Для некоторой ФАЛ, представленной с помощью карты Карно, можно записать несколько алгебраических выражений в дизъюнктивной или конъюнктивной форме.
При этом необходимо руководствоваться следующими правилами:
1) Все единицы (при записи функции в дизъюнктивной форме) и все нули (при записи функции в конъюнктивной форме) должны быть замкнуты в прямоугольные контуры.
2) Единичные контуры могут содержать несколько единиц, но не должны содержать нулей. Нулевые контуры могут содержать несколько нулей, но не должны содержать единиц.
3) Одноименные контуры могут накладываться один на другой, т.е. одна и та же единица (или ноль) может входить в несколько единичных (нулевых) контуров.
4) Число клеток в контуре должно быть равно 2i , где i = 0, 1, 2, …, n, т.е. число клеток в контуре выражается числами 0, 1, 2, 4, 8, 16, 32, …
5) Каждой единичной клетке отвечает конъюнкция входных переменных, которые определяют данную клетку. Каждой нулевой клетке отвечает дизъюнкция инверсий входных переменных, которые определяют данную клетку.
6) Выражения, которые отвечают контурам, не содержат тех переменных, чьи границы пересекаются площадью, ограниченной данным контуром.
7) Дизъюнктивная форма ФАЛ составляется в виде дизъюнкций конъюнкций, которые отвечают единичным контурам. Конъюнктивная форма ФАЛ составляется в виде конъюнкций дизъюнкций, которые отвечают нулевым контурам.
8) Если каждой клетке отвечает свой контур, то результирующее выражение представляет собой СДНФ или СКНФ данной ФАЛ. Минимальной ДНФ или КНФ отвечает минимальное количество единичных или нулевых контуров.
Пример для вышерассмотренной таблицы истинности:
| x2 | x1 | x0 | y = f(x2,x1,x0) | x2 | x1 | x0 | y = f(x2,x1,x0) |
 0 0 |
Минимальная ДНФ: Минимальная КНФ: