Определение результатов косвенных измерений и оценивание их погрешностей

Цель работы. Ознакомление с методикой выполнения косвенных измерений. Получение навыков определения результатов косвенных измерений, оценивания их погрешностей и представления результатов измерений.

4.1. Методические указания

4.1.1. Искомое значение физической величины 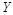при косвенном измерении находят на основании результатов измерений аргументов 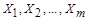, связанных с искомой величиной уравнением

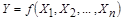. (4.1)

Функция 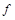должна быть известна из теоретических предпосылок или установлена экспериментально с погрешностью, которой можно пренебречь.

Результаты измерений аргументов и оценки их погрешностей могут быть получены из прямых, косвенных, совокупных или совместных измерений. Сведения об аргументах могут быть взяты из справочной литературы или технической документации.

4.1.2. Так как каждый аргумент функции (4.1) может быть измерен с соответствующей погрешностью, то задача расчета погрешности косвенного измерения сводится к суммированию погрешностей 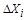результатов прямых измерений. При этом нужно учитывать, что доля отдельных погрешностей в результирующей погрешности может быть различной в зависимости от вида функции и соотношения аргументов .

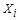При оценке погрешностей необходимо иметь в виду, что аргументы 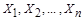могут быть взаимонезависимыми и взаимозависимыми.

4.1.3. При оценивании доверительных границ погрешностей результата косвенного измерения обычно принимают вероятность, равную 0,95 или 0,99. Использование других вероятностей должно быть обосновано.

4.1.4. При оценивании косвенно измеряемой величины и погрешностей результата измерения рассматриваются три возможности:

– линейная зависимость и отсутствие корреляции между погрешностями измерений аргументов;

– нелинейная зависимость и отсутствие корреляции между погрешностями измерения аргументов;

– наличие корреляции между погрешностями измерения аргументов при наличии рядов отдельных значений измеряемых аргументов.

4.1.5. При условии, что распределение случайных погрешностей результатов измерения аргументов не противоречит нормальному распределению, критерием отсутствия корреляционной связи между погрешностями результатов измерений аргументов является выполнение неравенства

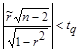, (4.2)

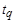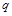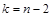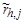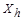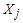где – коэффициент Стьюдента, соответствующий уровню значимости и числу степеней свободы , а оценка коэффициента корреляции между погрешностями аргументов и вычисляется по формуле

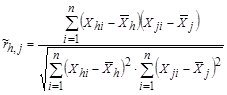, (4.3)

где 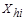, 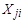– результаты 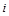-го измерения 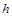-го и 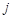-го аргументов; 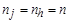– число измерений каждого из аргументов, 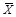– среднее арифметическое.

4.2. Косвенные измерения при линейной зависимости

4.2.1. При линейной зависимости искомое значение 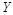связано с 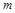измеряемыми аргументами 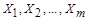уравнением

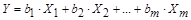, (4.3)

где 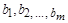– постоянные коэффициенты при аргументах 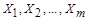соответственно.

4.2.2. При отсутствии корреляции между погрешностями измерений аргументов результат косвенного измерения 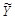вычисляют по формуле

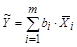, (4.4)

где 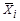– результат (итог) измерения аргумента 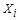; 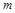– число аргументов.

4.2.3. Среднее квадратическое отклонение результата косвенного измерения 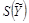вычисляют по формуле

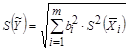, (4.5)

где 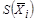– среднее квадратическое отклонение результата измерения аргумента .

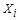4.2.4. Доверительные границы случайной погрешности результата косвенного измерения при условии, что распределения погрешностей результатов измерений аргументов не противоречат нормальным распределениям, вычисляют (без учета знака) по формуле

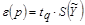, (4.6)

где 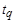– коэффициент Стьюдента, соответствующий доверительной вероятности 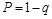и числу степеней свободы 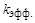(см. табл. 3.4), вычисляемому по формуле

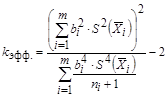, (4.7)

где 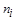– число измерений при определении аргумента .

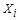4.2.5. Границы неисключенной систематической погрешности результата косвенного измерения вычисляют следующим образом.

4.2.5.1. Если неисключенные систематические погрешности результатов измерений аргументов заданы границами 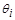, то доверительные границы неисключенной систематической погрешности результата косвенного измерения 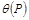(без учета знака) при вероятности 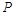вычисляют по формуле

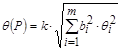, (4.8)

где 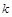– поправочный коэффициент, определяемый принятой доверительной вероятностью и числом 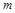составляющих .

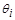При доверительной вероятности 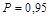поправочный коэффициент 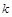принимают равным 1,1.

4.2.5.2. Если границы неисключенных систематических погрешностей результатов измерений аргументов заданы доверительными границами, соответствующими вероятностям 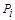, то границы неисключенной систематичекой погрешности результата косвенного измерения для вероятности 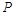вычисляют (без учета знака) по формуле

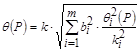. (4.9)

Для вероятности , .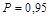

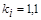4.2.6. Погрешность результата косвенного измерения оценивают на основе композиции распределений случайных и неисключенных систематических погрешностей.

4.2.6.1. Если 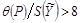, то за погрешность результата косвенного измерения принимают неисключенную систематическую составляющую погрешности измерения и ее границы вычисляют в соответствии с п. 4.2.5.

4.2.6.2. Если 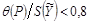, то за погрешность результата косвенного измерения принимают случайную составляющую погрешности измерения и ее границы вычисляют в соответствии с п. 4.2.4.

4.2.6.3. Если 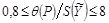, то доверительную границу погрешности результата косвенного измерения 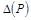вычисляют (без учета знака) по формуле

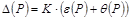, (4.10)

где K – коэффициент, зависящий от доверительной вероятности и от отношения .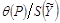

Значения коэффициента K в зависимости от отношения 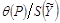для вероятности 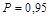приведены в табл. 4.1.

Таблица 4.1

Значения коэффициента K для определения доверительной границы

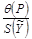	0,5	0,75
K	0,81	0,77	0,74	0,71	0,73	0,76	0,78	0,79	0,80	0,81

4.3. Косвенные измерения при нелинейной зависимости

4.3.1. Для косвенных измерений при нелинейных зависимостях и некоррелированных погрешностях измерений аргументов используют метод линеаризации.

4.3.2. Метод линеаризации предполагает разложение нелинейной функции в ряд Тейлора:

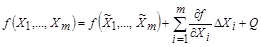, (4.11)

где 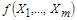– нелинейная функциональная зависимость измеряемой величины 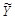от измеряемых аргументов 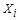; 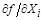– первая производная от функции 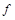по аргументу 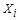, вычисленная в точке 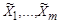; 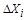– отклонение результата измерения аргумента 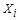от его среднего арифметического; 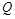– остаточный член.

Метод линеаризации допустим, если можно пренебречь остаточным членом .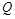

4.3.3. Остаточным членом

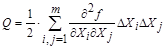(4.12)

пренебрегают, если

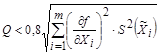, (4.13)

где 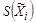– среднее квадратическое отклонение случайных погрешностей результата измерения 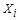– го аргумента.

Отклонения 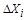при этом должны быть взяты из полученных значений погрешностей и такими, чтобы они максимизировали выражение для остаточного члена .

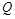4.3.4. Результат измерения 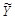вычисляют по формуле

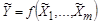. (4.14)

4.3.5. Среднее квадратическое отклонение случайной погрешности результата косвенного измерения 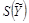вычисляют по формуле

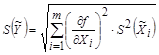. (4.15)

4.3.6. Доверительные границы случайной погрешности результата косвенного измерения при условии, что распределения погрешностей результатов измерения аргументов не противоречат нормальным распределениям, вычисляют в соответствии с п. 4.2.4, подставляя вместо коэффициентов 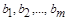первые производные 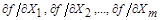, соответственно.

4.3.7. Границы неисключенной систематической погрешности результата косвенного измерения вычисляют в соответствии с п. 4.2.5, подставляя вместо коэффициентов 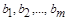первые производные 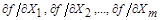, соответственно.

4.3.8. Погрешность результата косвенного измерения оценивают в соответствии с п. 4.2.6.

4.4. Косвенные измерения при наличии корреляции между погрешностями измерений аргументов

4.4.1. При наличии корреляции между погрешностями измерений аргументов для определения результатов косвенного измерения и его погрешности используют метод приведения, который предполагает наличие ряда отдельных значений измеряемых аргументов, полученных в результате многократных измерений. Этот метод можно также применять при неизвестных распределениях погрешностей аргументов. Более подробно с методом приведения можно ознакомиться в МИ 2083 – 90 «ГСИ. Измерения косвенные. Определение результатов измерений и оценивание их погрешностей».

4.5. Формы представления результата измерения

4.5.1. Если границы погрешности результата измерения симметричны, то результат измерения и его погрешность представляют в виде

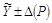. (4.16)

4.5.2. Если предполагают исследование и сопоставление результатов измерений или анализ погрешностей, то результат измерения и его погрешность представляют в виде

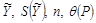, (4.17)

где n – число измерений того аргумента, при измерении которого выполнено минимальное число измерений.

4.6. Методика выполнения лабораторной работы

4.6.1. Косвенно измеряемой величиной в данном варианте лабораторной работы является удельное сопротивление 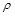некоторых металлов и сплавов.

Значение удельного сопротивления находится по формуле

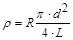, (4.18)

где 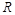– сопротивление проводника; 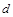и 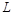– диаметр проводника и его длина.

4.6.2. Для нахождения удельного сопротивления получите у преподавателя проводники круглого сечения с известной длиной 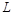, измеренной с известной погрешностью.

4.6.3. Ознакомьтесь с омметром, который будет использоваться для измерения сопротивления. Его тип и класс точности занесите в отчет.

4.6.4. Ознакомьтесь с микрометром, применяемым для измерения диаметра проводника и с методикой измерения линейных размеров с помощью микрометра. Его тип и класс точности занесите в отчет.

4.6.5. Выполните однократные измерения сопротивления проводника и его диаметра. Результаты измерений занесите в отчет.

4.6.6. Для получения результата косвенного измерения удельного сопротивления и его погрешности выполните необходимые расчеты, руководствуясь блок-диаграммой, представленной на рис. 4.1.

4.6.7. Необходимые расчеты и формулы занесите в отчет. Для записи результатов вычислений используйте табл. 4.2.

Таблица 4.2

Результаты вычислений при обработке косвенных измерений

№	Характеристики измеряемых величин	Измеряемые величины
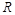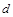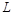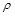	Измеренные значения аргументов	ˆ	ˆ	ˆ
	Границы неисключенных систематических погрешностей результатов измерений аргументов	ˆ	ˆ	ˆ
	Вычисленное значение результата косвенного измерения удельного сопротивления				ˆ
	Линеаризация уравнения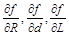
	Проверка остаточного члена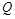
	Вычисление границы неисключенной систематической погрешности результата косвенного измерения				ˆ
	Вычисление погрешности результата косвенного измерения				ˆ
	Представление результата косвенного измерения				ˆ

4.8. Требования к отчету

Отчет должен содержать:

· сведения о цели и порядке выполнения работы;

· сведения об использованных методах измерений;

· сведения о характеристиках использованных средств измерений;

· схемы включения приборов при выполнении измерений и необходимые электрические схемы;

· данные, на основании которых выбирались средства измерений для выполнения каждого пункта задания;

· экспериментальные данные;

· полностью заполненные таблицы по рекомендованной форме, а также примеры расчетов, выполнявшихся при заполнении таблиц;

· анализ полученных данных и вывод об особенностях и качестве проведенных измерений и результатах проделанной работы.

Контрольные вопросы

1. Какие измерения называются косвенными?

2. Как оцениваются погрешности косвенных измерений при линейной зависимости между косвенно-измеряемой величиной и величинами, измеряемыми прямым методом?

3. Как оцениваются погрешности косвенных измерений при нелинейной зависимости между косвенно-измеряемой величиной и величинами, измеряемыми прямым методом?

4. Как оцениваются погрешности косвенных измерений при наличии корреляции между погрешностями измерений?

Лабораторная работа № 4.