Гамма-алгоритм (в общем виде) 4 страница

Определение. Фундаментальной матрицей сечений 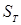(по дереву ) называется матрица, строками которой являются вектор-сечения, фундаментальные по дереву . Выделенному дереву на рисунке 4 отвечает фундаментальная матрица сечений, столбцы которой помечены номерами дуг всего графа, строки – номерами дуг дерева, точнее, номерами соответствующих фундаментальных сечений:

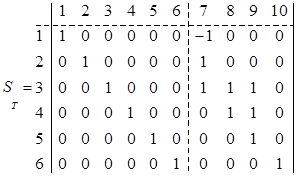
Определение. Фундаментальным циклом графа (по дереву ) называется всякий цикл, содержащий в точности одну дугу 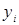кодерева 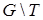и ориентированный согласно с направлением дуги 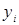. Каждая дуга кодерева однозначно задает фундаментальный цикл 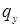, который дуга 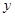замыкает на дереве .

Определение. Фундаментальной матрицей циклов 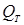(по дереву ) называется матрица, строки которой есть все фундаментальные вектор-циклы по дереву . Если для графа на рисунке фундаментальные вектор-циклы пометить номерами задающих дуг кодерева 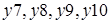, то фундаментальная матрица циклов такова:

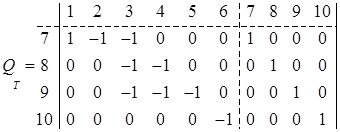
Для произвольных матрицы сечений и циклов данного графа справедливо соотношение ортогональности: .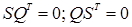

22.1.5 Алгоритм построения фундаментальной системы циклов

1. Построить любое остовное дерево исходного графа .

2. Добавить к некоторое ребро , которое является ребром графа, но не принадлежит остову.

3. После такого добавления образуется цикл .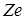

4. Все циклы 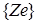(соответствующие всем ребрам, взятым не из остова) образуют фундаментальную систему циклов.

22.2 Раскраска графов

22.2.1 Раскраска вершин

Определение. Раскраской вершин графа называется назначение цветов его вершинам. Обычно цвета – это числа 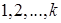. Тогда раскраска является функцией, определенной на множестве вершин графа и принимающей значения в множестве 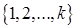. Раскраску можно также рассматривать как разбиение множества вершин 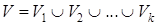, где 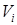– множество вершин цвета 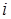. Множества называют цветными классами. Раскраска называется правильной, если каждый цветной класс является независимым множеством. Иначе говоря, в правильной раскраске любые две смежные вершины должны иметь разные цвета. Задача о раскраске состоит в нахождении правильной раскраски данного графа в наименьшее число цветов. Это число называется хроматическим числом графа и обозначается .

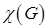22.2.2 Хроматическое число

Рассмотрим задачу: при каких условиях вершины графа можно раскрасить так, чтобы каждое ребро было инцидентно вершинам разного цвета? Нас больше всего интересует вопрос, какие графы можно раскрасить с соблюдением определенных условий, чем вопрос, сколькими способами можно выполнить это раскрашивание.

Пусть граф не имеет петель; тогда называется -раскрашиваемым, если каждой его вершине можно приписать один из цветов таким образом, чтобы никакие две смежные вершины не оказались одного цвета. Если граф является -раскрашиваемым, но не является 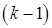-раскрашиваемым, назовем его 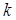-хроматическим, а число назовем хроматическим числом. На рис. 22.722изображен 4-хроматический (и, следовательно, 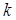-раскрашиваемый граф при 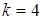) граф; цвета обозначены греческими буквами.

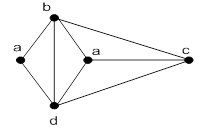
Рисунок 22.7 – 4-х хроматический граф

Для удобства будем предполагать, что все графы не содержат петель. Однако будем допускать существование кратных ребер, так как они не влияют на наши рассуждения.

Ясно, что 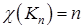, и, следовательно, легко построить графы со сколь угодно большим хроматическим числом. С другой стороны, нетрудно видеть, что 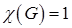тогда и только тогда, если – вполне несвязный граф, и что 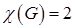тогда и только тогда, если – двудольный (биохроматический) граф, отличный от вполне несвязного графа.

Теорема 22.1. Если наибольшая из степеней вершин графа равна 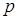, то этот граф 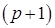-раскрашиваем. При этом хроматическое число графа равно 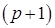только в двух случаях: во-первых, если граф является полным и, во-вторых, если 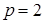и при этом данный граф содержит контур нечетной длины. Во всех остальных случаях хроматическое число графа не превосходит максимальной степени вершин.

Доказательство. Проведем индукцию по числу вершин в . Пусть – граф с вершинами; если из него удалить произвольную вершину 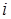вместе с инцидентными ей ребрами, то в оставшемся графе будет 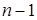вершин, причем степени вершин по-прежнему не превосходят 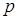. По предположению индукции этот граф 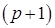-раскрашиваем, отсюда получится 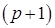-раскраска для , если окрасить вершину 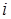цветом, отличным от тех, которыми окрашены смежные с ней вершины, а их не более чем p.

Теорема (Брукса). Пусть – простой связный граф, не являющийся полным; если наибольшая из степеней его вершин равна 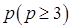, то он 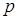-раскрашиваем.

Доказательство. Проведем индукцию по числу вершин графа . Предположим, что имеет вершин. Если при этом степень какой-нибудь его вершины меньше 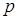, дальше можно рассуждать, как в доказательстве теоремы 1, и все будет закончено. Поэтому без потери общности можно считать граф регулярным степени .

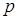Выберем произвольную вершину 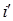и удалим ее, вместе с инцидентными ей ребрами. Останется граф с 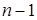вершинами, в котором наибольшая из степеней вершин не превосходит 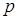. По предположению индукции этот граф 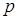-раскрашиваем. Теперь окрасим вершину 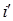в один из имеющихся 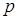цветов. Как и раньше, считаем, что смежные с 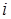вершины 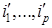расположены вокруг 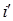по часовой стрелке и окрашены в различные цвета , .

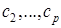Определяя подграфы 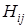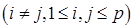_, когда 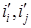лежат в разных компонентах графа 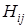. Таким образом, можно считать, что при любых данных 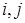вершины 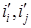связаны простой цепью, целиком лежащей в 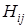. Обозначим компоненту графа 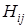, содержащую вершины 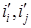, через .

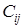Ясно, что если вершина 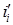– смежная более чем с одной вершиной цвета 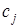, то существует цвет, отличный от 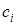, не приписанный никакой из вершин, смежных с 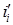. Тогда вершину 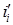можно окрасить в этот цвет, что, в свою очередь, позволит окрасить вершину 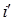в цвет 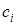и закончить на этом доказательство теоремы. Если этот случай не имеет места, то используем аналогичное рассуждение, чтобы показать, что каждая вершина из 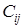(отличная 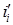от и от 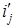) должна иметь степень 2. Предположим, что 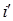— первая вершина простой цепи из 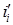в 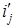, которая имеет степень больше 2; тогда 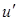можно перекрасить в цвет, отличный от 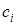или 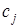, нарушая тем самым свойство, что 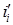и 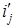связаны простой цепью, целиком лежащей в 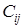. Поэтому мы можем считать, что для любых 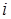и 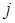компонента 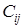состоит только из простой цепи, соединяющей вершину 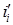c .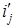

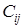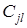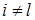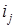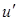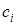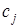Заметим теперь, что две простые цепи вида и , где , можно считать пересекающимися только в вершине , так как если – другая точка пересечения, то ее можно перекрасить в цвет, отличный от или , или 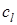, а это противоречит факту, что 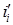, 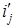связаны простой цепью.

Для завершения доказательства выберем (если это возможно) две несмежные вершины 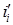, 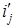и допустим, что 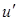– вершина цвета 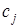, смежная с 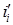. Поскольку 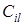– простая цепь (для любого 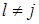), можно поменять между собой цвета вершин в этой цепи, не затрагивая раскраску остальной части графа. Но это приводит к противоречию, потому что тогда 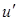будет общей вершиной простых цепе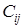й и 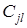. Отсюда следует, что нельзя выбрать две вершины 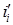и 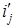несмежными, и поэтому должен быть полным графом 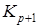. А так как это не допускается условием теоремы, то все возможные случаи рассмотрены.

Некоторые практические задачи связанные с раскраской ребер графа , что считается правильным, если каждые 2 смежных ребра (инцидентных одной вершине) раскрашиваются в разные цвета.

Определение. Наименьшее число цветов для правильной раскраски называется хроматическим классом 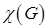графа или индексом. Так как раскрашивание графа сводится к некоторому графу 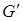, который называется дуальнымпо отношению к , потому, что 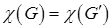– хроматический класс равен хроматическому числу дуального графа. 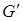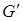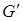Это свойство дуального графа соответствующим образом его определяет: вершины дуального графа находятся в соответствии с ребрами , и 2 вершины у графа соединенные ребром, тогда и только тогда 2 ребра у смежные.

Определение.Если граф имеет хроматическое число 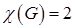, то его называют бихроматическим графом. Любое раскрашивание 2 красками разбивает вершины на 2 множества 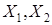, посередине каждого множества вершины попарно несмежные (или независимы).

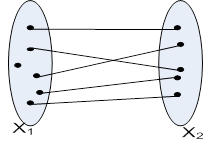
Рисунок 22.8 – Две плоскости бихроматического графа

Теорема Кенига.Граф называется бихроматическим тогда и только тогда, когда все его циклы имеют четную длину.

Доказательство. Следующие доказательства графа эквивалентные:

1. Все замкнутые маршруты имеют четную длину.

2. Все циклы имеют четную длину.

3. Все простые циклы имеют четную длину.

Пусть граф бихроматический. Раскрашиваем его 2 цветами. Концы каждого цепи четной длины имеют одинаковый цвет, нечетной – разные, поэтому замкнутые маршруты (циклы) нечетной длины отсутствуют. Пусть все замкнутые маршруты графа имеют четную длину. Разукрасим в цвет 1 а одну вершину 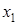_, потом в цвет 2 – ее окружение (множество смежных вершин), в цвет 1 – окружение вершин цвета 2 и т.д. За конечное число граф будет раскрашен в цвет 1 и 2.

22.2.3 Гипотеза о четырех красках

Уже сто с лишним лет математики пытаются доказать гипотезу четырех красок. В этом направлении был достигнут значительный прогресс. В печати появилось сообщение (K.Appel, W.Haken, Every planar map is four colorable, Bull. of Amer. Math. Soc., 82, \No\,5 (sept. 1976)), что гипотезу четырех красок удалось обосновать с использованием ЭВМ.

Сформулируем без доказательства несколько относящихся к этой проблеме результатов.

1. Если гипотеза четырех красок не верна, то любой опровергающий ее пример будет очень сложным. Известно, например, что всякий планарный граф, имеющий менее 52 вершин, 4-раскрашиваем.

2. Любой не содержащий треугольников планарный граф 3-раскрашиваем (теорема Греча).

3. Если попытаться доказать гипотезу четырех красок, то достаточно доказать ее для гамильтоновых планарных графов (довольно неожиданный результат Уитни).

Возникновение гипотезы четырех красок исторически связано с раскрашиванием географических карт. Если имеется карта с изображением нескольких стран, то интересно узнать, сколько понадобится цветов для такой раскраски этих стран, чтобы никакие две соседние страны не были окрашены в один и тот же цвет. Возможно, самая привычная форма гипотезы четырех красок такова: любую карту можно раскрасить с помощью четырех красок.

Определение.Назовем карту -раскрашиваемой, если ее грани можно раскрасить красками так, чтобы никакие две смежные грани, то есть грани, границы которых имеют общее ребро, не были одного цвета. Там, где можно запутаться, будем использовать термин вершинно -раскрашиваемой, имея в виду -раскрашиваемость в описанном выше смысле. Например, изображенный ниже граф является 3-раскрашиваемым и вершинно 4-раскрашиваемым.

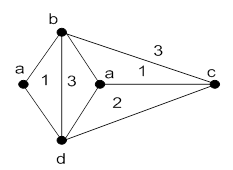
Рисунок 22.9 – Граф 3-раскрашиваемый и вершинно 4-раскрашиваемый.

Теперь сформулируем гипотезу четырех красок для карт: всякая карта 4-раскрашиваема.

Теорема 22.2. Карта является 2-раскрашиваемой тогда и только тогда, если G представляет собой эйлеров граф.

Доказательство. Любую вершину 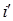из должно окружать четное число граней, так как их можно раскрасить в два цвета. Отсюда следует, что степень каждой вершины четна, и поэтому – эйлеров граф.

22.2.4 Двудольные и -дольные графы

Определение.Неориентированный граф 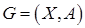называют двудольным, если множество его вершин может быть разбито на такие два подмножества 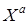и 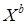, что каждое ребро имеет один конец в 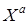, а другой в 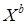(рис. 22.10,а).

Ориентированный граф называется двудольным, если его неориентированный двойник – двудольный граф (рис. 22.10,б,в).

Двудольный граф 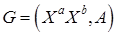называют полным, если для любых двух вершин 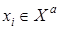и 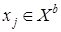существует ребро 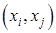в 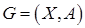(рис. 22.10,г).

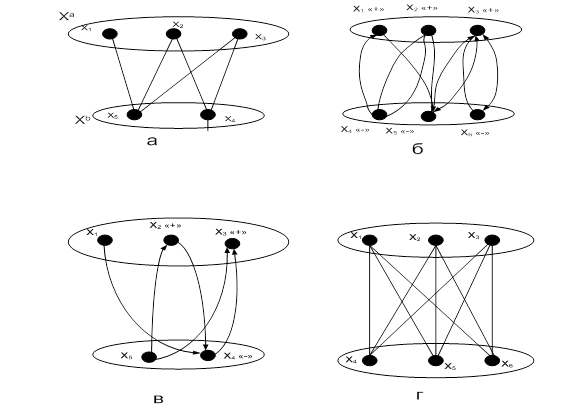
Рисунок 22.10 – Двудольные графы: а, б, в – двудольные графы; г – полный двудольный граф

Теорема о двудольности.Граф 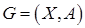является двудольным тогда и только тогда, когда он не содержит циклов нечетной длины.

Доказательство:смотри теорему Кенига о бихроматических графах.

22.3 Контрольные вопросы и задания