Генерування випадкових чисел.

Насправді, випадкові числа – це фізичні процеси.

Детерміновані алгоритми генерують лише псевдовипадкові числа.

Вимоги до послідовності випадкових чисел:

1. Випадковість.

2. Непередбачуваність.

Для перевірки на випадковість використовують такі критерії:

a) однорідність розподілу;

b) незалежність.

Незалежність – ні одне зі значень послідовності не повинне поч.. виводитись з інших значень (математичний момент).
Непередбачуваність – не можна передбачити наступне число (статистичний момент).

Генератор псевдовипадкових чисел

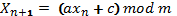
m > 0, модуль порівняння;

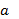– множник;

с – приріст;

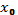– початкове число (породжуюче).

0 ≤ а < m

0 ≤ c < m

0 ≤ 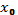< m

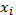0 ≤ < m

На значення повного періоду впливає m.

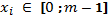
Вимоги до якості генератора псевдовипадкових чисел

1. Функція повинна бути функцією повного періоду.

2. Функція повинна ефективно реалізовуватись в рамках 32-бітної арифметики.

3. Згенерована послідовність повинна поводитись як випадкова.

Криптографічно генеровані випадкові числа

1. Шифр. покази лічильника.

2. OFB – режим зворотнього зв’язку за виходом.

ANSI X9.17

(В основі алгоритм – потрійний DES з 2-ома ключами)

Vi

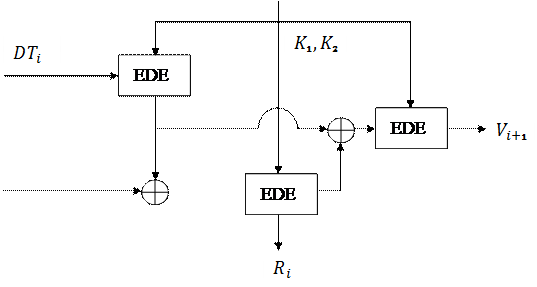
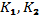- ключі шифрування. Подаються на кожній стадії.

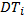– дата і час.

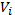– початкове значення для і-тої стадії генерування (вихід попередньої стадії).

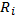- випадкове число.

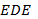– потрійний DES.

На виході – 64-бітне число.

BBS – генератор

Блюм – блюм – шуб!

p ≡ q ≡ 3 mod 4 – будь-які 2 великі числа

p ≠ q

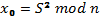
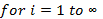
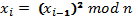
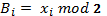
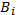- вихід функції (1 біт)

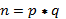
S – взаємно просте з N, випадкове.

BBS– криптографічно захищений генератор псевдовипадкових бітів. Задовільняє критерій наступного біта (next-bit test), тобто не існує поліном. алгоритму, який за першими k-бітами вих. послідовності може передбачати k+1 –й біт з ймовірністю, суттєво більшою ½.

Лекція №6 Криптографія з відкритим ключем

- Алгоритми математично не доведені.

- Дуже повільні алгоритми.

Загальна логіка роботи

К

А с=Ес(m) B

Ku Kr

Public Private

KuA KuB одним шифруємо іншим розшифровуємо

KrA KrB

A->B: C = E_KUB(М)

E_KRA(m) – зашифрувати може тільки А, прочитати зможуть всі.

Нема проблеми з поширенням ключів і з цифровим підписом.

Особливість алгоритма

З точки зору обчислень не можливо обчислити приватний ключ, знаючи алгоритм і публічний ключ.

Крім того деякі алгоритми мають таку особливість що будь-який з пари ключів може служити для шифрування і тоді інший використовується для розшифрування.

Загальна схема

1. Кожна система генерує пару з двох ключів.

2. Кожна система публікує свій відкритий ключ. Інший ключ не розголошується.

3. Якщо А хоче написати В, то він шифрує повідомлення публічним ключем В.

4. Отримавши повідомлення, В розшифровує його своїм приватним ключем.

	Традиційне	Асиметричне
1.Треба для роботи	1 алгоритм, 1 ключ	1 алгоритм, 2 ключа
2.Треба для захисту	1. Ключ має бути в таємниці. 2. Повинно бути не можливо розшифрувати повідомлення тільки за самим повідомленням. 3. Знання алгоритму і зразків тексту не повинні давати змогу відновити ключ.	1. Один з двох ключів має бути в таємниці. 2. Повинно бути не можливо розшифрувати повідомлення тільки за самим повідомленням. 3. Знання алгоритму, одного з ключів і зразку повідомлення не повинні бути достатніми для відновлення іншого ключа.

E_KUB(ES) || E_KS(М) - така схема використовується

Область застосування

1. Шифрування/дешифрування(не великі об’єми).

2. Цифровий підпис.

3. Обмін ключами.