Минимальная ДНФ (МДНФ) булевой функции
Одна из её тупиковых ДНФ, которой соответствует наименьшее значение критерия минимизации (индекса простоты) ДНФ.
Минимальная КНФ (МКНФ) булевой функции
Одна из её тупиковых КНФ, которой соответствует наименьшее значение критерия минимизации (индекса простоты) КНФ.
Минимально полный базис
Система функций называется минимально полным базисом, если удаление из неё любой функции превращает эту систему в неполную.
Минтерм  -го ранга
-го ранга
Член дизъюнктивной нормальной формы, представляющий собой элементарную конъюнкцию  букв.
букв.
Минтерм  -го ранга
-го ранга
То же, что и конституента единицы.
Монотонная функция
Функция 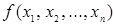 называется монотонной, если для любых двух наборов
называется монотонной, если для любых двух наборов 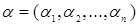 и
и 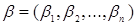 , находящихся в отношении предшествования (нестрогого порядка), имеет место и неравенство
, находящихся в отношении предшествования (нестрогого порядка), имеет место и неравенство 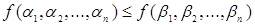 .
.
Неполное дизъюнктивное склеивание
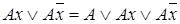 , где
, где  - некоторая элементарная конъюнкция переменных;
- некоторая элементарная конъюнкция переменных;  - булева переменная.
- булева переменная.
Неполное конъюнктивное склеивание
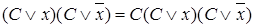 , где
, где 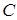 - некоторая элементарная дизъюнкция переменных;
- некоторая элементарная дизъюнкция переменных;  - булева переменная.
- булева переменная.
Несократимая полная система булевых функций,
Полная система булевых функций, из которой нельзя исключить ни одной булевой функции без потери свойств полноты.
Номер интерпретации (кортежа)
Десятичный эквивалент двоичного представления интерпретации.
Нулевой элемент (нуль)
Элемент 0 из множества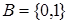 .
.
Область определения булевой функции
Множество слов длины  , которые представляют собой всевозможные наборы из
, которые представляют собой всевозможные наборы из  двоичных цифр и их общее количество равно
двоичных цифр и их общее количество равно 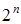 .
.
Ослаблено функционально полная система
Система функций 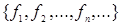 из
из 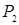 , суперпозицией которых может быть представлена любая функция из некоторого множества булевых функций и в которой допускаются константы 0 и 1.
, суперпозицией которых может быть представлена любая функция из некоторого множества булевых функций и в которой допускаются константы 0 и 1.
То же, что и функционально полная система булевых функций в слабом смысле.
Отрицание
Функция 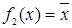 , равная 1, когда аргумент принимает значение 0, и равная 0 при аргументе 1.
, равная 1, когда аргумент принимает значение 0, и равная 0 при аргументе 1.
Переключательная функция
То же, что и булева функция.
Покрытие функции
Множество  , состоящее из импликант функции
, состоящее из импликант функции  , если каждое единичное значение функции
, если каждое единичное значение функции  покрывается единицей хотя бы одной импликанты из множества
покрывается единицей хотя бы одной импликанты из множества  .
.
Полином Жегалкина
Конечная сумма по модулю 2 попарно различных элементарных конъюнкций над множеством переменных 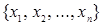 .
.
Полная система импликант функции
То же, что и покрытие функции.
Полная система имплицент функции
Множество  , состоящее из имплицент функции
, состоящее из имплицент функции  , если каждое единичное значение функции
, если каждое единичное значение функции  покрывается нулем хотя бы одной имплиценты из множества
покрывается нулем хотя бы одной имплиценты из множества  .
.
