Функции, родственные функции СРЗНАЧ

Функция СРЗНАЧА

Синтаксис;

СРЗНАЧА (значение1, значение2,...)

Вычисляет среднюю арифметическую значений, заданных в списке аргументов, которые могут включать текст и логические значения.

Помимо чисел в расчете могут участвовать текст и логические значения, такие, как ИСТИНА и ЛОЖЬ.

Функция УРЕЗСРЕДНЕЕ

УРЕЗСРЕДНЕЕ (массив; доля)

Рассчитывает среднюю арифметическую усеченного множества данных путем отбрасывания заданного процента данных с экстремальными значениями. В результате из анализа исключается заданный процент выбросов данных.

Аргументы:

Массив: массив усредняемых значений;

доля: доля точек данных, исключаемых из вычислений. Например, если доля равна 0,2, то из множества данных, содержащих 40 точек, исключаются 8 точек (40 * 0,2), 4 точки с наибольшими значениями и 4 точки с наименьшими значениями в множестве данных.

Функция УРЕЗСРЕДНЕЕ рассчитывает значение средней арифметической при уменьшенном размахе вариации (размах вариации рассчитывается как разность между наибольшим и наименьшим значениями признака, см. описание функции МАКС).

Размах вариации позволяет судить об устойчивости значений варьирующего признака. Вместе с тем к существенным недостаткам размаха вариации можно отнести то обстоятельство, что очень низкое и очень высокое значения признака по сравнению с основной массой его значений в совокупности могут быть обусловлены какими-либо сугубо случайными обстоятельствами (т. е. эти значения являются аномальными в совокупности или, иначе, выбросами). В этих случаях выбросы могут существенно исказить статистические оценки. Поэтому следует очистить совокупность от выбросов, прежде чем приступать к обработке данных.

Внимание! Исключать «подозрительные» выбросы из совокупности нужно очень осторожно. Необоснованное исключение «подозрительных» выбросов может привести к существенному искажению статистических оценок. В связи с этим возникает необходимость решения задачи — считать ли данный «подозрительный» выброс принадлежащим данной генеральной совокупности или аномальным, подлежащим исключению из выборки.

Исключение крайних оценок (выбросов) широко используется в методах коллективной экспертной оценки, в частности в методе «Дельфи». Так, при рассмотрении оценок группы экспертов оценка, слишком сильно отличающаяся от других, может быть исключена из дальнейшего рассмотрения, несмотря на то, что она может оказаться более верной, чем остальные. Правда, подобные отклонения, по мнению авторов «Дельфи» компенсируются тем, что эксперта, не согласного с большинством, просят высказать причины несогласия. Все эксперты имеют возможность ознакомиться с его доводами и могут принять во внимание или отвергнуть их, переоценить свое мнение или остаться при нем. Так что оценка, далеко отстоящая от других, отбрасывается фактически лишь в том случае, если эксперту не удается достаточно веско аргументировать свою точку зрения.

Функция СРГАРМ

Синтаксис;

СРГАРМ (число1; число2;...)

Результат;

Рассчитывает среднюю гармоническую множества данных.

Число1, число.2,……… - аргументы, для которых вычисляется средняя гармоническая.

Замечания;

· если какой-либо из аргументов меньше или равен 0, то функция СРГАРМ помещает в ячейку значение ошибки #ЧИСЛО!;

· средняя гармоническая всегда меньше средней геометрической.

Математико-статистическая интерпретация;

Средняя гармоническая — это величина, обратная к средней арифметической обратных величин. Формула для средней гармонической имеет следующий вид:

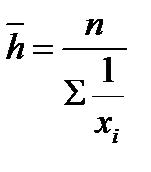(невзвешенная средняя гармоническая).

Функция СРГАРМ рассчитывает значение невзвешенной средней гармонической, ее нельзя использовать для расчета взвешенной средней гармонической.

Как видно, средняя гармоническая является превращенной формой средней арифметической. Вместо гармонической всегда можно рассчитать среднюю арифметическую, но для этого сначала нужно определить веса отдельных значений признака f _i.

Функция СРГЕОМ

Синтаксис;

СРГЕОМ (число1; число2;...)

Результат;

Рассчитывает среднюю геометрическую значений массива положительных чисел.

Замечания;

· аргументы должны быть числами или именами, массивами или ссылками, содержащими числа;

· если аргумент, который является массивом или ссылкой, содержит текстовые, логические значения или пустые ячейки, то такие значения игнорируются; однако ячейки с нулевыми значениями учитываются;

· если какой-либо из аргументов меньше или равен 0, то функция СРГЕОМ помещает в ячейку значение ошибки #ЧИСЛО!.

Математико-статистическая интерпретация;

Одной из формул, по которой может рассчитываться средний показатель, является средняя геометрическая:

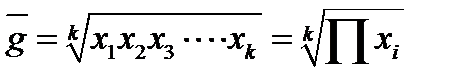
Этой средней удобно пользоваться, когда внимание уделяется не абсолютным разностям, а отношениям двух чисел. Поэтому средняя геометрическая используется в расчетах среднегодовых темпов роста.

Средний темп роста является сводной обобщающей характеристикой интенсивности изменения уровней ряда динамики. Он показывает, во сколько раз в среднем за единицу времени изменился уровень динамического ряда. Необходимость исчисления среднего темпа роста возникает вследствие того, что темпы роста из года в год колеблются.