Функционально полная система булевых функций
Система функций 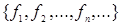 из
из 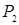 (где
(где 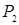 − множество всех возможных булевых функций, зависящих от любого числа переменных), в которой любая булева функция может быть записана в виде формулы через функции этой системы (в виде суперпозиции функций из этой системы).
− множество всех возможных булевых функций, зависящих от любого числа переменных), в которой любая булева функция может быть записана в виде формулы через функции этой системы (в виде суперпозиции функций из этой системы).
Функционально полная система булевых функций в слабом смысле
Система функций 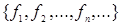 из
из 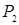 , суперпозицией которых может быть представлена любая функция из некоторого множества булевых функций и в которой допускаются константы 0 и 1.
, суперпозицией которых может быть представлена любая функция из некоторого множества булевых функций и в которой допускаются константы 0 и 1.
То же, что и ослаблено функционально полная система.
Функция, сохраняющая единицу (1)
Булева функция 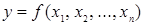 , которая на единичном наборе равна 1, т.е.
, которая на единичном наборе равна 1, т.е.  .
.
Функция, сохраняющая ноль (0)
Булева функция 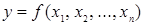 , которая на нулевой наборе равна 0, т.е.
, которая на нулевой наборе равна 0, т.е.  .
.
Эквивалентные формулы
Формулы, представляющие одну и ту же функцию (то же, что и равносильные формулы).
Элементарная дизъюнкция
Дизъюнкция любого числа булевых переменных, взятых с отрицанием или без него, в которой каждая переменная встречается не более одного раза.
Элементарная конъюнкция
Конъюнкция любого числа булевых переменных, взятых с отрицанием или без него, в которой каждая переменная встречается не более одного раза.
Логика высказываний и логика предикатов
 -местный предикат
-местный предикат
Предикат, содержащий  переменных (
переменных (  аргументов) (обозначается
аргументов) (обозначается  ).
).
Аксиомы логики высказываний
Аксиомами логики высказываний является некоторое множество общезначимых формул логики высказываний.
Антецедент
В импликации 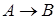 высказывание
высказывание  называется антецедентом.
называется антецедентом.
То же, что и условие, посылка.
Атом (в логике высказываний)
Высказывание, которое соответствует простому повествовательному предложению, т.е. не имеет составных частей.
То же, что и элементарное высказывание, атомарная формула.
Атом (в логике предикатов)
Если  -
-  -местный предикат и
-местный предикат и  - термы, то
- термы, то  называется атомом.
называется атомом.
То же, что и элементарная формула логики предикатов.
Атомарная формула
То же, что и элементарное высказывание, атом.
Вывод в исчислении высказывания
Всякая последовательность 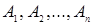 формул такая, что для любого
формул такая, что для любого 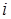 формула
формула 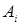 есть либо аксиома, исчисления высказываний, либо непосредственное следствие каких-либо предыдущих формул, полученных по правилу вывода.
есть либо аксиома, исчисления высказываний, либо непосредственное следствие каких-либо предыдущих формул, полученных по правилу вывода.
Выполнимые формулы
Все формулы, не относящиеся к противоречивым, образуют множество выполнимыхформул.
Высказывание
Утверждение или повествовательное предложение, о котором можно сказать, истинно оно или ложно, но ни то и другое одновременно.
