Сведение недетерминированного автомата к детерминированному.

Построение праволинейной грамматики.

Исходными заданиями для курсовой работы являются две таблицы - табл. 1 и

2-й правила вывода R, приведенные ниже.

В табл. 1 в первую строку записывается перечисление 18 Символов С_i, во

вторую строку записываются первые 18 символов фамилии, имени и отчества

студента, а в третью - заносится для каждого из 18 символов строки символ

из алфавита {х_1, х₂, х₃, х₄, х₅, х₆, х₇} в соответствии с табл. 2.

Таблица 1

ci

C1

C2

C3

C4

C5

C6

C7

C8

C9

C10

C11

C12

C13

C14

C15

C16

C17

C18

si

xi

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

Таблица 2

А

Б

В

Г

Д

Е

Ж

З

И

Й

К

Л

М

Н

О

П

X1

X5

X2

X4

X6

X6

X4

X3

X3

X0

X7

X0

X3

X7

X4

X5

Р

С

Т

У

Ф

Х

Ц

Ч

Ш

Щ

Ь

Ы

Э

Ю

Я

-

X0

X4

X5

X7

X2

X5

X1

X2

X2

X0

X6

X1

X1

X3

X7

X5

Для курсовой работы задана формальная грамматика G=(V_t, V_n, S, R), где V_t={c₁, c₂, c₃, ... , c₈} - терминальный словарь; V_n= {S,A,B,C,D,E,F } - нетерминальный словарь; S, принадлежащее множеству V_n - начальный символ грамматики; R - множество правил вывода, которые имеют следующий вид:

S→c₁ c₂ c₃ A; S→c₁ c₄ c₅ B; S→c₆ C; S→c₇ F; A→c₈ D; A→c₉;

B→c₈ E; B→c₉; C→c₈ E; C→c₉; D→c₁₀ S; D→c₁₁; E→c₁₀ S;

E→c₁₁; F→c₁₂ c₁₃ c₁₄ c₁₅; F→c₁₆ c₁₃ c₁₄ c₁₅; F→c₁₇ c₁₈ c₁₅;

Эта грамматика, являющаяся праволинейной, приводится к виду

G’=(V’t,V’_n, S, R’), где V’_t={x₀, x_1,х₂, ... , х₇} - новый терминальный словарь;

R' - множество правил вывода, получаемых из заданных заменой символов

из алфавита V_t символами из алфавита V’_t в соответствии с табл. 1.

В данном примере они имеют вид

S→x₄ x₀ x₁A | x₄ x₇ x₇B | x₄C | x₅F; A→x₄D | x₆; B→x₄E | x₆; C→x₄E | x₆;

D→x₀S | x₄; E→x₀S | x₄; F→x₆ x₀ x₅ x₂ | x₀ x₀ x₅ x₂ | x₁ x₂ x₂

Здесь | - металингвистический символ (связка), читаемый как «или».

Переход от праволинейной грамматики к автоматной.

Этот этап выполняется путем расширения нетерминального словаря способом, вытекающим из возможности преобразования праволинейной грамматики в автоматную G’’=(V_t’, V_n’’, S, R’’). Для рассматриваемого примера получим множество R’’ правил вывода:

S→x₄ S₁; S₁→x₀ S₂; S₂→x₁ A; S→x₄ S₃; S₃→x₇ S₄; S₄→x₇ B; S→x₄ C; S→x₅ F;

A→x₄ D; A→x₆; B→x₄ E; B→x₆; C→x₄ E; C→x₆; D→x₀ S; D→x₄;

E→x₀ S; E→x₄; F→x₆ F₁; F₁→x₀ F₂; F₂→x₅ F₃; F₃→x₂; F→x₀ F₄; F₄→x₀ F₅;

F₅→x₅ F₆; F₆→x₂; F→x₁ F₇; F₇→x₂ F₈; F₈→x₂

Таким образом, нетерминальный словарь теперь имеет вид

V_n’’ = {S₁, S₂, S₃, S₄, А, В, С, D, E, F, F₁, F₂, F₃, F₄, F₅, F₆, F₇, F₈} и его

мощность | V_n | равна 19.

Построение недетерминированного конечного автомата.

Рассмотрим недетерминированный конечный распознающий автомат

A=(Q, х, δ, q₀, q_k), где Q - множество внутренних состояний; х - входной алфавит; δ - отображение δ:x*Q→P(Q); P(Q) - множество подмножеств из Q; q₀, принадлежащее Q - начальное состояние; q_k, принадлежащее Q - заключительное состояние, q_k≠q₀.

Этот автомат зададим следующим образом. Поставим в соответствие символам нетерминального словаря V_n’’ состояния из Q, в том числе нетерминалу S - начальное состояние q₀, и добавим заключительное состояние q_k, в котором автомат оказывается, если цепочка предъявляемых ему символов принадлежит L(G’’). Таким образом, мощность | Q | множества Q равна | Q | = | V_n’’ | +1=20.

В данном примере нетерминальным символам, указанным в строках 1 и 3 таблицы 3, соответствует состояния автомата, перечисленные в строках 2 и 4.

Таблица 3

S	S1	S2	S3	S4	A	B	C	D	E
q0	q1	q2	q3	q4	q5	q6	q7	q8	q9
F	F1	F2	F3	F4	F5	F6	F7	F8	-
q10	q11	q12	q13	q14	q15	q16	q17	q18	q19

Заключительное состояние обозначено через q₁₉.

Поставив правилам вывода в соответствие переходы автомата, получим таблицу переходов недетерминированного конечного автомата (табл. 4) и граф переходов (рис. 1).

Таблица (4) переходов недетерминированного конечного автомата.

Рисунок 1

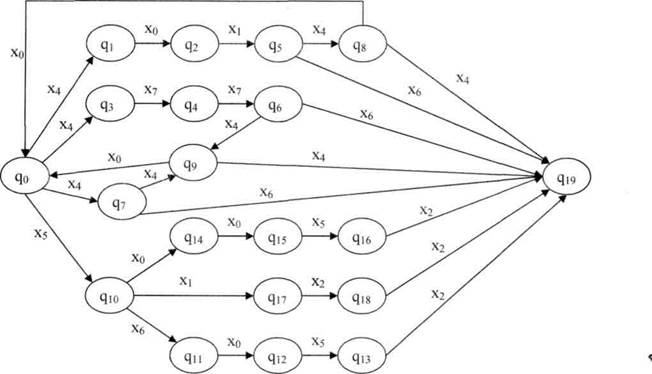
Таблица 4

q	x0	x1	x2	x3	x4	x5	x6	x7
q0					q1,q3,q7	q10
q1	q2
q2		q5
q3								q4
q4								q6
q5					q8		q19
q6					q9		q19
q7					q9		q19
q8	q0				q19
q9	q0				q19
q10	q14	q17					q11
q11	q12
q12						q13
q13			q19
q14	q15
q15						q16
q16			q19
q17			q18
q18			q19
q19

Сведение недетерминированного автомата к детерминированному.

Недетерминированность автомата локально проявляется в том, что из
некоторого его состояния q_i исходят несколько дуг, помеченных одним и тем
же символом X_j. В этом случае она устраняется склеиванием двух состояний
в одно. В результате применения этого алгоритма от автомата на рис.1 можно
перейти к эквивалентному детерминированному автомату, таблица
переходов которого приведена в табл. 5, а соответствующий ей граф
переходов - на рис. 2. Таблица 5

q	x0	x1	x2	x3	x4	x5	x6	x7
q0					q1,3,7	q10
q1,3,7	q2				q9		q19	q4
q2		q5
q4								q6
q5					q8		q19
q6					q9		q19
q8	q0				q19
q9	q0				q19
q10	q14	q17					q11
q11	q12
q12						q13
q13			q19
q14	q15
q15						q16
q16			q19
q17			q18
q18			q19
q19

Рисунок 2

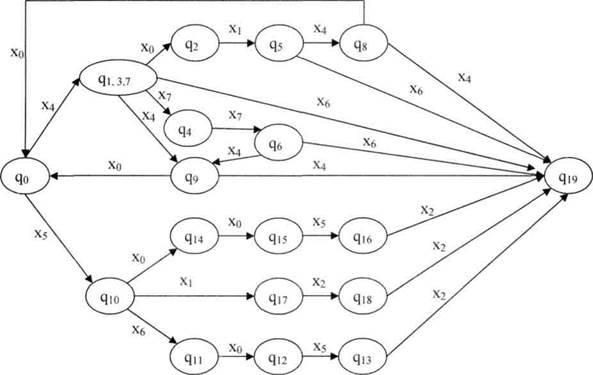
Минимизация автомата.

Построение минимального (но числу состояний) автомата, эквивалентного полученному в предыдущем разделе полностью определенному детеминированному конечному автомату, осуществляется в два этапа. На первом находится разбиение состояний автомата на классы эквивалентности, а на втором строится минимальный (иначе - приведенный) автомат. В начале составляется треугольная таблица (табл.6), клетки которой соответствуют всем парам (q_i, q_j), i≠j рабочих состояний. Она заполняется следующим образом. Если для рабочих состояний q_i и q_j в таблице существует входной символ х_k, при котором переход из q_i осуществляется в одно из рабочих состояний, а из q_j - в состояние ошибки, то состояния q_j и q_j не эквивалентны, и соответствующая им клетка помечается крестом. Иначе, если какие-либо две строчки табл.5 содержат разное число рабочих состояний или отличаются позициями, занимаемыми рабочими состояниями, то обозначающие это строки состояния не эквивалентны. В противном случае в клетку таблицы 6 с координатами q_i, q_j запишем каждую пару состояний (q_v, q_w), в которые автомат может перейти из q_i и q_j при подаче одного и того же входного символа.

Таблица 6

1,3,7

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

X

1,3,7

Витоге невычеркнутые клетки табл. 6 соответствуют всем парам

эквивалентных состояний. Класс эквивалентности образуется состояниями,

которые попарно эквивалентны. В данном случае получается 4 класса

эквивалентности: {q₅, q₆}, {q₈, q₉,}, {q₁₂, q₁₅},{q₁₃, q₁₆, q₁₈}. Каждое

состояние, не вошедшее ни в один класс эквивалентности, эквивалентно

лишь само себе и само образует этот класс. В нашем примере к

перечисленным классам необходимо добавить еще 9 классов

эквивалентности: q₀, q_1,3,7, q₂, q₄, q₁₀, q₁₁, q₁₄, q₁₇, q₁₉,

Состояния минимального автомата обозначим буквами r с индексами:

r₀={q₅, q₆}, r₁={q₈, q₉}, r₂={q₁₂, q₁₅}, r₃={q₁₃, q₁₆, q₁₈}, r₄={q_1,3,7},

r₅={q₂}, r₆={q₄}, r₇={q₁₀}, r₈={q₁₁}, r₉={q₁₄}, r₁₀={q₁₇}, r₁₁={q₁₉}, r₁₂={q₀}.

Минимальный автомат содержит, таким образом, 13 состояний, не считая состояния ОШИБКА. Граф переходов этого автомата приведен на рис. 3, а таблица переходов - в табл. 7

Рисунок 3

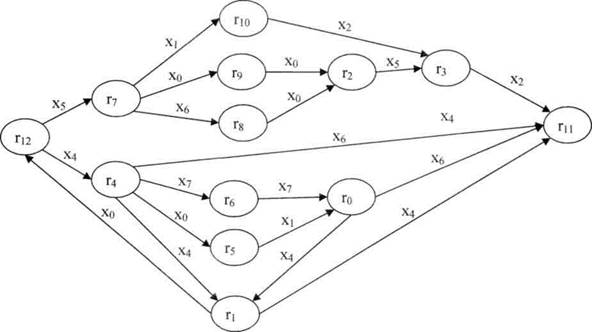Таблица 7