Высказывательная переменная

Переменная, которая может принимать два значения: «истина» и «ложь», т.е. принимать истинностное значение.

Двуместный предикат

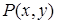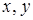Предикат, имеющий две переменные (может обозначаться, например, , где − переменные).

Дедуктивный вывод

Вывод формулы из формулы , основанный на том, что является логическим следствием .

Дизъюнкция высказываний и

Высказывание 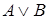, которое ложно тогда и только тогда, когда ложны оба высказывания и .

Дистрибутивные свойства кванторов

;

,

где − любой из кванторов или .

Закон де Моргана для кванторов

; .

Закон замены связанной переменной

, .

Заключение

В импликации 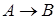высказывание называется заключением.

То же, что и следствие, консеквент.

Замкнутая формула

Формула логики предикатов, которая не имеет свободных переменных.

Импликация высказываний и

Высказывание 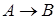, которое ложно тогда и только тогда, когда истинно, а ложно.

Индивидуальный символ

Терм-константа называется индивидуальным символом.

То же, что и предметная константа.

Интерпретация высказывания

Приписывание истинностных значений атомам, из которых построено высказывание.

Интерпретация формулы логики предикатов

Интерпретация формулы состоит из элементов непустой предметной области, значений всех констант, функциональных символов и предикатов, встречающихся в .

Истинностное значение

Абстрактный объект («истина» или «ложь»), сопоставляемый высказыванию в зависимости от того, является это высказывание истинным или ложным. Обозначается: «истина» − И, Т (True) или 1, „ложь” – Л, F (False) или 0.

Исчисление высказываний

Исчисление высказываний, являясь формальной системой, представляет собой пример аксиоматической теории и один из возможных способов формализации логики высказываний.

Исчисление предикатов

Формальная система в логике предикатов.

Квантор всеобщности

Символ называется квантором всеобщности.

То же, что и квантор общности.

Квантор общности

То же, что и квантор всеобщности.

Квантор существования

Символ называется квантором существования.

Коммутативные свойства кванторов

; .

Консеквент

В импликации 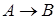высказывание называется консеквентом.

То же, что и следствие, заключение.

Конъюнкция высказываний и

Высказывание 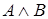, которое истинно тогда и только тогда, когда истинны оба высказывания и .

Логика высказываний

Алгебраическая структура 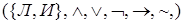) с носителем – двоичным множеством { : «Ложь», : «Истина»}, операциями (логическими связками): « » – конъюнкция, « 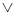» – дизъюнкция, « 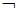» – отрицание, « 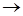» – импликация, «~» – эквивалентность.