Раткие теоретические сведения

АЛГОРИТМЫ ПРИНЯТИЯ РЕШЕНИЙ НА ОСНОВЕ

НЕЧЕТКОЙ ЛОГИКИ

ель работы

Целью выполнения работы является:

· закрепление знаний в области нечеткой логики и механизмов принятия решений на её основе;

· ознакомление с пакетом математического моделирования Fuzzy Toolbox в среде Matlab;

· реализация нечеткого алгоритма принятия решений с помощью Matlab.

раткие теоретические сведения

Нечеткая логика – это математическая наука, служащая расширением классической логики и основанная на концепции частичной истинности. Понятия нечетких множеств (fuzzy sets) и нечеткой логики (fuzzy logic) впервые были предложены американским ученым Лотфи Заде (Lotfi Zadeh) в 1965 г. в статье “Нечеткие множества”, опубликованной в журнале “Информатика и управление”.

Основные преимущества систем на основе нечеткой логики:

· возможность оперирования нечеткими входными данными: например, значениями, которые невозможно задать однозначно («сильно уязвимый», «довольно дорогой» и т.п.);

· возможность нечеткой формализации критериев оценки и сравнения: оперирование критериями "большинство", "возможно", преимущественно";

· возможность проведения качественных оценок как входных данных, так и выходных результатов;

· возможность проведения имитационного моделирования сложных динамических систем и их сравнительный анализ с заданной степенью точности.

Нечетким логическим выводом(fuzzy logic inference) называется аппроксимация зависимости Y = f(x₁, x₂, …, x_n) выходной лингвистической переменной от входных лингвистических переменных и получение заключения в виде нечеткого множества, с использованием базы знаний, содержащей правила вида «Если …, то…».

Механизм логического вывода состоит, в общем случае, из следующих этапов:

1) фаззификация – определение степеней уверенности, т.е. значения каждой из функций принадлежности терма при заданных значениях входных переменных x_k (k = 1, …, n);

2) нечеткий вывод – состоит из двух этапов:

· определение уровней «отсечения» для левой части каждого из правил, т.е. значения функций принадлежности для левых частей каждого правила («предпосылок»). В большинстве случаев, это либо максимум, либо минимум из степеней уверенности термов, вычисленных на этапе фаззификации (логические «ИЛИ», «И»);

· определение «усеченных» функций принадлежности. Для этого значения функций принадлежности предпосылок объединяются с соответствующими функциями принадлежности из правых частей правил по правилу «логического И»;

3) нечеткая композиция – определение результирующей функции принадлежности всей совокупности правил, т.е. объединение полученных усеченных функций (обычно по правилу «логического ИЛИ»);

4) дефаззификация – приведение к «четкости», используя результирующую функцию принадлежности. Основным методом деффазификации является центроидный (centroid) – нахождение центра тяжести плоской фигуры, ограниченной осями координат и графиком функции принадлежности нечеткого множества;

В качестве примера рассмотрим процедуру принятия решения о необходимости выделения затрат на модернизацию системы защиты информации (СЗИ).

1. Сформулируем набор нечетких логических переменных:

· уровень угроз x = {Низкий (S), Средний (M), Высокий (L)};

· уязвимость ресурсов y = {Невысокая (S), Высокая (L)};

· затраты на модернизацию z = {Низкие (S), Высокие (L)}.

2. Построим графики функций принадлежности для этих переменных (рис. 3):

в

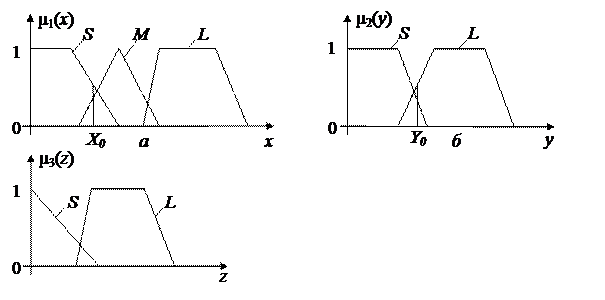
Рис. 3. Функции принадлежности для уровня угроз, уязвимости и

затрат на модернизацию СЗИ: а – уровень угроз; б – уязвимость ресурсов; в – затраты на модернизацию.

3. Сформулируем правила, регламентирующие работу системы принятия решений:

ЕСЛИ Уровень угроз = «НИЗКИЙ» И Уязвимость ресурсов = «НЕВЫСОКАЯ» ТО Затраты на модернизацию = «НИЗКИЕ»

Полный список всех правил, с указанием соответствующих значений нечетких переменных x, y и z приведен в табл. 1:

Таблица 1

База правил

x y	S	M	L
S	S	L	L
L	S	S	L

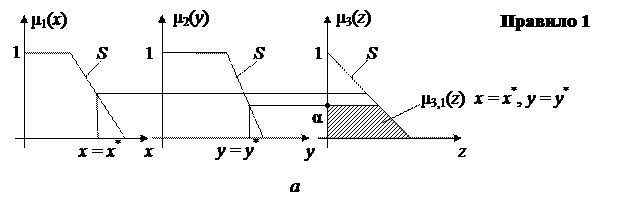
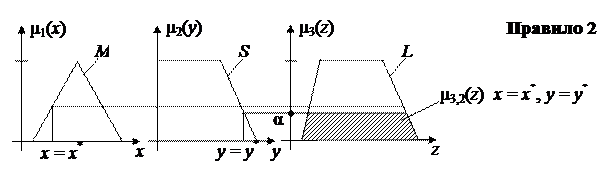
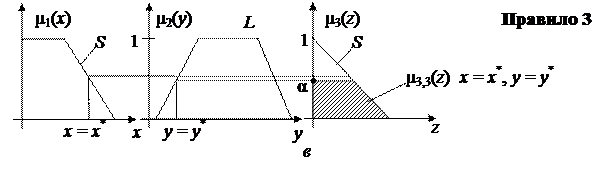
4. Построим графическое представление механизма логического вывода для конкретных значений входных переменных x = x^* и y = y^* (рис. 4)

б

5. Определим результирующую функцию принадлежности совокупности правил 1 - 4, используя при дефаззификации центроидный метод (рис. 5).

α3 = max { α1, α3, α4}

Рис. 5. Определение функции принадлежности

для выходной переменной и дефаззификация

2.3. Основные сведения о пакете Matlab

Matlab – пакет прикладных программ для решения задач численного анализа созданный компанией The MathWorks. Пакет позволяет визуализировать математические функции и экспериментальные данные, реализовывать вычислительные алгоритмы, конструировать графический интерфейс пользователя для решения специфических задач, а также через специальные интерфейсы взаимодействовать с другими языками программирования и программами.

При загрузке Matlab появляется основное окно программы (рис. 6), состоящее из следующих частей:

1) меню;

2) панель инструментов;

3) Launch Pad – список доступных инструментальных пакетов;

4) Command History – история команд;

5) Command Window – окно команд.

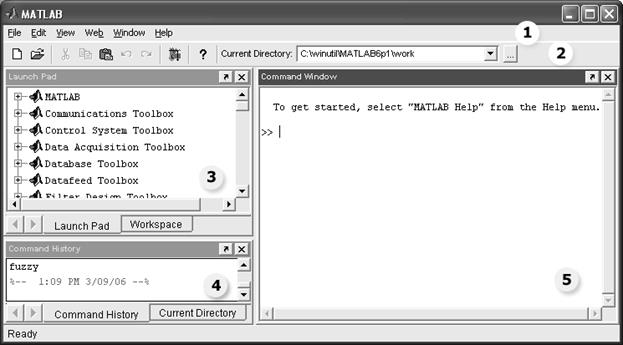
Рис. 6. Основное окно Matlab

Для выполнения сложных расчетов, подобных работе с алгоритмами нечеткой логики, необходимо использовать дополнительные инструментальные пакеты. Их можно запустить с помощью Launch Pad либо из окна команд. Инструментальный пакет для работы с алгоритмами нечеткой логики запускается с помощью команды fuzzy.

Основными элементами окна Fuzzy Toolbox (рис. 7) являются:

1) меню;

2) настройка входных и выходных функций принадлежности;

3) настройка методов сложения множеств на разных этапах.

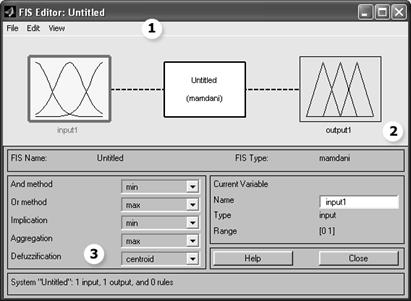
Рис. 7. Окно настроек Fuzzy Logic Toolbox

Для добавления входных переменных необходимо воспользоваться командой меню «Edit → Add Variable → Input». Для удаления входной переменной необходимо выбрать её и воспользоваться командой меню «Edit → Remove Selected Variable».

Для изменения параметров входных и выходных функций принадлежности, необходимо выполнить двойной клик на одной из входных/выходных переменных или воспользоваться командой меню «Edit → Membership Functions» (рис. 8).

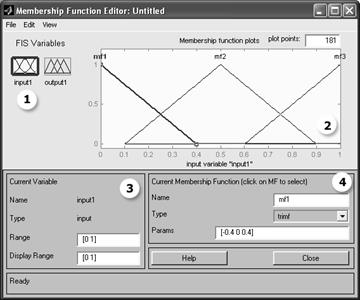
Рис. 8. Изменение параметров функций принадлежности

На рис. 8 цифрами 1 - 4 обозначены:

1 – поле выбора переменной, для которой требуется изменить параметры функции принадлежности;

2 – редактор функции принадлежности;

3 – поле настройки параметров переменной:

· range – отрезок значений, которые может принимать переменная;

· display range – отрезок значений, отображаемый на графике;

4 – поле настройки параметров выбранной функции принадлежности:

· name – название функции приналежности;

· type – вид функции (trimf – треугольная, trapmf – трапецеидальная, gauss – гауссова);

· params – параметры функции.

Для добавления дополнительных функций принадлежности для выбранной переменной, необходимо воспользоваться меню «Edit → Add MFs», где необходимо задать вид функции и количество добавляемых функций.

Для удаления функции принадлежности необходимо выбрать её и воспользоваться меню «Edit → Remove Selected MF».

Для редактирования правил необходимо воспользоваться меню «Edit → Rules» (рис. 9).

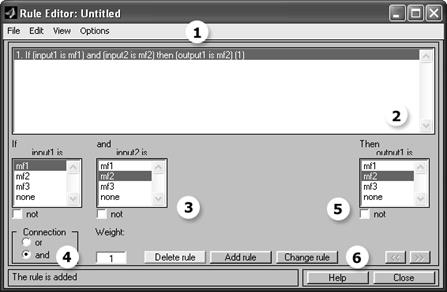
Рис. 9. Редактор правил

На рис. 9 цифрами 1 - 6 обозначены:

1 – меню;

2 – список созданных правил;

3 – область выбора условий левой части правила
(предпосылок);

4 – область выбора связи между условиями предпосылок (или/и);

5 – область выбора результирующей функции принадлежности;

6 – набор управляющих кнопок:

«Delete Rule» – удалить правило, выбранное в списке созданных правил;

«Add Rule» – добавить правило;

«Change Rule» – изменить правило, выбранное в списке созданных правил.

Для создания нового правила необходимо задать условия левой части правила, результирующую функцию и нажать на кнопку «Add Rule».

Для удаления правила, необходимо выбрать его в списке и нажать кнопку «Delete Rule».

Для проверки работы механизма нечеткого вывода необходимо воспользоваться меню «View → Rules».

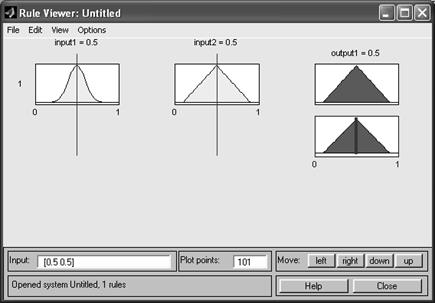
Рис. 10. Просмотр механизма нечеткого вывода

В строке «Input» необходимо задать значения входных переменных и нажать клавишу ввода. В строке «Output» будет указано выходное значение и будут отображены графики соответствующих функций принадлежности.

Рассмотрим пример использования пакета Matlab для моделирования приведенной выше задачи модернизации СЗИ.

1. Запустим Fuzzy Logic Toolbox с помощью команды fuzzy.

2. Добавим вторую входную лингвистическую переменную, используя меню «Edit → Add Variable → Input» (рис. 11):

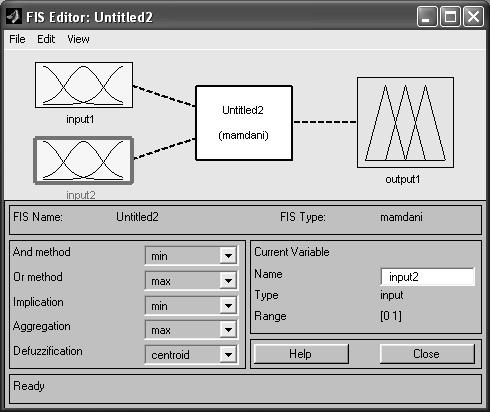
Рис. 11. Добавление лингвистической переменной

3. Отредактируем параметры функций принадлежности в соответствии с условиями задачи (рис. 12):

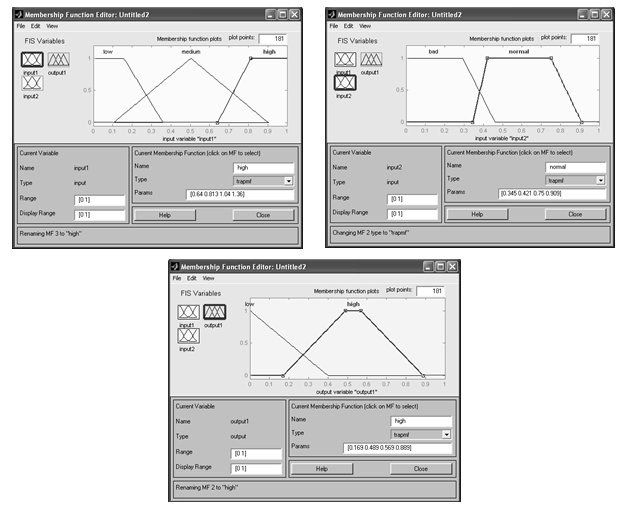
Рис. 12. Настройка параметров функций принадлежности

4. Сформулируем набор правил (рис. 13):

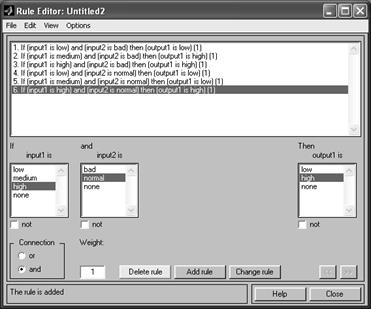
Рис. 13. Окно редактора правил

5. Просмотрим результаты моделирования механизма принятия решений, используя меню «View → Rules» (рис. 14):

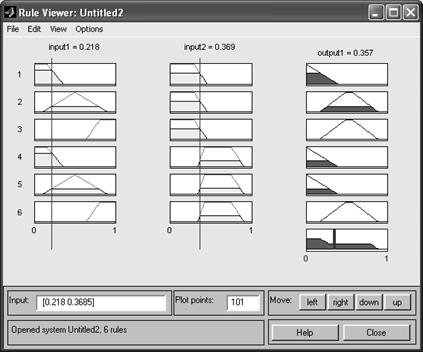
Рис. 14. Окно результатов моделирования

Вариант 1

1.1

Входные лингвистические переменные	Выходная лингвистическая переменная
x – Средняя заработная плата клиента y – Продолжительность работы на последнем месте	z – Степень финансового доверия

1.2

Входные лингвистические переменные	Выходная лингвистическая переменная
x – Возраст y – Социальное положение	z – Степень социального доверия

1.3

Входные лингвистические переменные	Выходная лингвистическая переменная
x – Степень финансового доверия y – Степень социального доверия	z – Максимальный размер потребительского кредита

Вариант 2

2.1

Входные лингвистические переменные	Выходная лингвистическая переменная
x – Уровень осадков y – Среднесуточная температура	z – Скорость таяния снежного покрова

2.2

Входные лингвистические переменные	Выходная лингвистическая переменная
x – Максимальный ожидаемый уровень воды в водохранилище y – Площадь бассейна водохранилища	z – Объем водяного спуска

2.3

Входные лингвистические переменные	Выходная лингвистическая переменная
x – Скорость таяния снежного покрова y – Объем водяного спуска	z – Ожидаемый уровень половодья

Вариант 3.

3.1

Входные лингвистические переменные	Выходная лингвистическая переменная
x – Качество сценария y – Качество игры актеров	z – Качество режиссерской работы

3.2

Входные лингвистические переменные	Выходная лингвистическая переменная
x – Бюджет фильма y – Уровень спецэффектов	z – Зрелищность фильма

3.3

Входные лингвистические переменные	Выходная лингвистическая переменная
x – Качество режиссерской работы y – Зрелищность фильма	z – Величина кассовых сборов фильма

Вариант 4.

4.1

Входные лингвистические переменные	Выходная лингвистическая переменная
х – Качество преподавания y – Качество лабораторно-методической базы	z – Качество учебного процесса

4.2

Входные лингвистические переменные	Выходная лингвистическая переменная
x – Уровень мотивации студента y – Степень сообразительности студента	z – Средняя успеваемость студента

4.3

Входные лингвистические переменные	Выходная лингвистическая переменная
x – Качество учебного процесса y – Средняя успеваемость студента	z – Уровень усвоения знаний

Вариант 5

5.1

Входные лингвистические переменные	Выходная лингвистическая переменная
x – Уровень финансовых вложений y – Срок окупаемости проекта	z – Степень эффективности вложения средств

5.2

Входные лингвистические переменные	Выходная лингвистическая переменная
x – Квалификация персонала y – Качество материальной базы	z – Качество выполненной работы

5.3

Входные лингвистические переменные	Выходная лингвистическая переменная
x – Степень эффективности вложения средств y – Качество выполненной работы	z – Эффективность проекта