Гамма-алгоритм (в общем виде) 5 страница
1. Дайте определение маршрута, пути, цепи, цикла в графе. Приведите практические примеры этих определений.
2. Дайте определение цикломатического числа. Охарактеризуйте его свойства.
3. Как задается цикломатическая матрица графа?
4. Что называется раскраской вершин графа.
5. Что называется хроматическим числом.
6. Какой граф является бихроматическим графом?
7. Приведите теорема Кенига о бихроматическом графе.
8. Что называется хроматическим классом 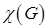 графа или индексом?
графа или индексом?
9. Сформулируйте гипотезу четырех красок для карт.
10. Какие графы являются двудольными и  -дольными?
-дольными?
Лекция 23. Транспортные сети и потоки. Их свойства
23.1 Кратчайшие расстояния и пути в графах
Пусть  – неориентированнный граф.
– неориентированнный граф.
Определение. Маршрутом в  называется такая конечная или бесконечная последовательность ребер, что каждые два соседних ребра имеют концевую точку. Причем, одно и то же ребро
называется такая конечная или бесконечная последовательность ребер, что каждые два соседних ребра имеют концевую точку. Причем, одно и то же ребро 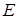 может встречаться в маршруте несколько раз.
может встречаться в маршруте несколько раз.
Определение. Циклическим маршрутом называется такой маршрут, начальная и конечная точки которого совпадают.
Определение. Цепью называется маршрут, в котором каждое его ребро встречается не более одного раза; вершины в цепи могут повторяться и более одного раза. Любой участок цепи является цепью. Нециклическая цепь является простой цепью, если в ней никакая вершина не повторяется.
Для ориентированного графа можно вводить как неориентированные маршруты, цепи и простые цепи, не принимая во внимание ориентации ребер, так и ориентированные маршруты (цепи, простые цепи), в которых все ребра находятся в направлении их ориентации. Ориентированные цепи также называют путями.
23.2 Алгоритм Дейкстры поиска кратчайших путей
Алгоритм Дейкстры решает задачу о кратчайших путях из одной вершины для взвешенного ориентированного графа 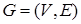 с исходной вершиной
с исходной вершиной 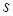 , в котором веса всех рёбер неотрицательны (
, в котором веса всех рёбер неотрицательны ( 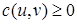 для всех
для всех 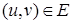 ).
).
Формальное объяснение
В процессе работы алгоритма Дейкстры поддерживается множество 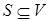 , состоящее из вершин
, состоящее из вершин  , для которых
, для которых 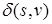 уже найдено. Алгоритм выбирает вершину
уже найдено. Алгоритм выбирает вершину 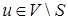 с наименьшим
с наименьшим 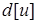 , добавляет
, добавляет  к множеству
к множеству  и производит релаксацию всех рёбер, выходящих из
и производит релаксацию всех рёбер, выходящих из  , после чего цикл повторяется. Вершины, не лежащие в
, после чего цикл повторяется. Вершины, не лежащие в  , хранятся в очереди
, хранятся в очереди  с приоритетами, определяемыми значениями функции
с приоритетами, определяемыми значениями функции 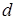 . Предполагается, что граф задан с помощью списков смежных вершин.
. Предполагается, что граф задан с помощью списков смежных вершин.
Неформальное объяснение
Каждой вершине из 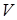 сопоставим метку — минимальное известное расстояние от этой вершины до
сопоставим метку — минимальное известное расстояние от этой вершины до 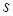 . Алгоритм работает пошагово — на каждом шаге он «посещает» одну вершину и пытается уменьшать метки. Работа алгоритма завершается, когда все вершины посещены.
. Алгоритм работает пошагово — на каждом шаге он «посещает» одну вершину и пытается уменьшать метки. Работа алгоритма завершается, когда все вершины посещены.
Инициализация. Метка самой вершины 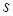 полагается равной 0, метки остальных вершин — бесконечности. Это отражает то, что расстояния от
полагается равной 0, метки остальных вершин — бесконечности. Это отражает то, что расстояния от 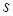 до других вершин пока неизвестны. Все вершины графа помечаются как непосещенные.
до других вершин пока неизвестны. Все вершины графа помечаются как непосещенные.
Шаг алгоритма. Если все вершины посещены, алгоритм завершается. В противном случае из еще не посещенных вершин выбирается вершина  , имеющая минимальную метку. Рассматриваем всевозможные маршруты, в которых
, имеющая минимальную метку. Рассматриваем всевозможные маршруты, в которых  является предпоследним пунктом. Вершины, соединенные с вершиной
является предпоследним пунктом. Вершины, соединенные с вершиной  ребрами, назовем соседями этой вершины. Для каждого соседа рассмотрим новую длину пути, равную сумме текущей метки
ребрами, назовем соседями этой вершины. Для каждого соседа рассмотрим новую длину пути, равную сумме текущей метки  и длины ребра, соединяющего
и длины ребра, соединяющего  с этим соседом. Если полученная длина меньше метки соседа, заменим метку этой длиной. Рассмотрев всех соседей, пометим вершину
с этим соседом. Если полученная длина меньше метки соседа, заменим метку этой длиной. Рассмотрев всех соседей, пометим вершину  как посещенную и повторим шаг.
как посещенную и повторим шаг.
Пример.Рассмотрим работу алгоритма на примере графа, показанного на рисунке. Пусть требуется найти расстояния от 1-й вершины до всех остальных.
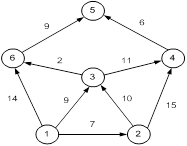
Рисунок 23.1
Кружками обозначены вершины, линиями — пути между ними (ребра графа). В кружках обозначены номера вершин, над ребрами обозначена их «цена» — длина пути. Рядом с каждой вершиной красным обозначена метка — длина кратчайшего пути в эту вершину из вершины 1.
Первый шаг. Рассмотрим шаг алгоритма Дейкстры для нашего примера. Минимальную метку имеет вершина 1. Ее соседями являются вершины 2, 3 и 6.
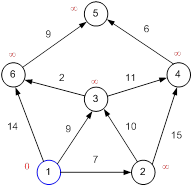
Рисунок 23.2
Первый по очереди сосед вершины 1 — вершина 2, потому что длина пути до нее минимальна. Длина пути в нее через вершину 1 равна кратчайшему расстоянию до вершины 1 + длина ребра, идущего из 1 в 2, то есть 0 + 7 = 7. Это меньше текущей метки вершины 2, поэтому новая метка 2-й вершины равна 7.
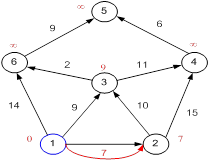
Рисунок 23.3
Аналогичную операцию проделываем с двумя другими соседями 1-й вершины — 3-й и 6-й.
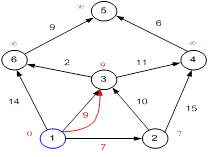
Рисунок 23.4
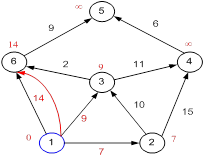
Рисунок 23.5
Все соседи вершины 1 проверены. Текущее минимальное расстояние до вершины 1 считается окончательным и пересмотру не подлежит (то, что это действительно так, впервые доказал Дейкстра). Вычеркнем её из графа, чтобы отметить, что эта вершина посещена.
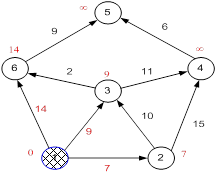
Рисунок 23.6
Второй шаг. Шаг алгоритма повторяется. Снова находим «ближайшую» из непосещенных вершин. Это вершина 2 с меткой 7.
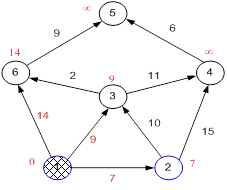
Рисунок 23.7
Снова пытаемся уменьшить метки соседей выбранной вершины, пытаясь пройти в них через 2-ю. Соседями вершины 2 являются 1, 3, 4.
Первый (по порядку) сосед вершины 2 — вершина 1. Но она уже посещена, поэтому с 1-й вершиной ничего не делаем.
Следующий сосед вершины 2 — вершины 4 и 3. Если идти в неё через 2-ю, то длина такого пути будет = кратчайшее расстояние до 2 + расстояние между вершинами 2 и 4 = 7 + 15 = 22. Поскольку 22<∞, устанавливаем метку вершины 4 равной 22.
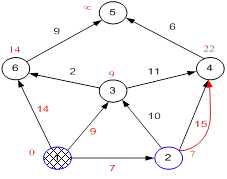
Рисунок 23.8
Ещё один сосед вершины 2 — вершина 3. Если идти в неё через 2, то длина такого пути будет = 7 + 10 = 17. Но текущая метка третьей вершины равна 9<17, поэтому метка не меняется.
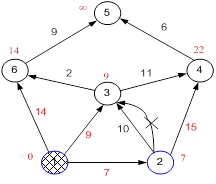
Рисунок 23.9
Все соседи вершины 2 просмотрены, замораживаем расстояние до неё и помечаем ее как посещенную.
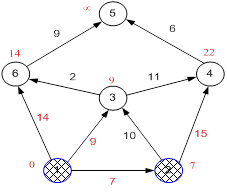
Рисунок 23.10
Третий шаг. Повторяем шаг алгоритма, выбрав вершину 3.
Дальнейшие шаги. Повторяем шаг алгоритма для оставшихся вершин (Это будут по порядку 6, 4 и 5).
Завершение выполнения алгоритма. Алгоритм заканчивает работу, когда вычеркнуты все вершины. Результат его работы: кратчайший путь от вершины 1 до 2-й составляет 7, до 3-й — 9, до 4-й — 20, до 5-й — 20, до 6-й — 11.
Для удобства можно заполнять таблицу:
| Вершины | 1(*) | 2(*) | 3(*) | 6(*) | 4(*) | |
| 0* | ||||||
| ∞ | 7* | |||||
| ∞ | 9* | |||||
| ∞ | ∞ | 20* | ||||
| ∞ | ∞ | ∞ | ∞ | 20* | ||
| ∞ | 11* |
По строкам располагаем номера вершин. По столбцам – вершины, у которых на данном шаге минимальная метка. В ячейках таблицы располагаем метки вершин на каждом шаге алгоритма. Изменяются только те метки, для которых пересчитывается расстояние. У всех остальных вершин метки остаются прежние. Вершина, получившая минимальную метку (*), больше не рассматривается. Если в ячейках находятся одинаковые значения меток, выбирается любая из них.
Поскольку алгоритм Дейкстры всякий раз выбирает для обработки вершины с наименьшей оценкой кратчайшего пути, можно сказать, что он относится к жадным алгоритмам.
23.3 Алгоритмы поиска кратчайших путей между всеми парами вершин графа
23.3.1 Алгоритм Флойда
Формулировка задачи. Дан непустой взвешенный граф с произвольными весами ребер. Требуется найти кратчайшие длины путей между всеми парами вершин графа, если в графе нет циклов отрицательной длины или обнаружить наличие таких циклов.
Алгоритм
Инициализация структур данных.
Строится матрица 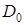 размерности
размерности 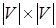 , элементы которой определяются по правилу:
, элементы которой определяются по правилу: 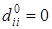 ;
;
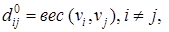 если в графе существует ребро (дуга)
если в графе существует ребро (дуга) 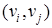 ;
;
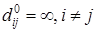 , если нет ребра (дуги)
, если нет ребра (дуги) 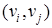 .
.
Основная часть алгоритма:
Выполнять цикл, завершение которого наступает по выполнению одного из двух условий: либо количество шагов цикла равно 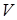 , либо был обнаружен цикл отрицательной длины. Шаги цикла нумеруются с нуля. Шаг цикла будем обозначать переменной
, либо был обнаружен цикл отрицательной длины. Шаги цикла нумеруются с нуля. Шаг цикла будем обозначать переменной 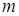 .
.
Строится матрица с индексом равным номеру шага, обозначим его через 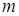 , в которой элементы определяются через элементы матрицы предыдущего шага по следующим формулам:
, в которой элементы определяются через элементы матрицы предыдущего шага по следующим формулам:
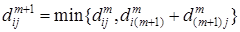 , где
, где 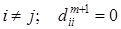 . (*)
. (*)
Если 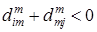 для какого-то
для какого-то 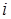 , то в графе существует цикл (контур) отрицательной длины, проходящий через вершину
, то в графе существует цикл (контур) отрицательной длины, проходящий через вершину 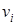 .
.
По завершению работы данного алгоритма, элементы матрицы равны длинам кратчайших путей между соответствующими вершинами.
Поиск путей
Если требует найти сами пути, то перед началом работы алгоритма построим матрицу P с начальными значениями элементов 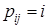 . Каждый раз, когда на шаге (1) значение
. Каждый раз, когда на шаге (1) значение 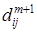 будет уменьшаться в соответствии с (*) (т.е. когда
будет уменьшаться в соответствии с (*) (т.е. когда 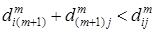 ), выполним присваивание
), выполним присваивание 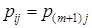 . В конце работы алгоритма матрица P будет определять кратчайшие пути между всеми парами вершин: значение pij будет равно номеру предпоследней вершины в пути между
. В конце работы алгоритма матрица P будет определять кратчайшие пути между всеми парами вершин: значение pij будет равно номеру предпоследней вершины в пути между 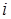 и
и 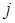 (либо
(либо 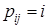 , если путь не существует).
, если путь не существует).
Примечаниe: если граф - неориентированный, то все матрицы 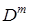 являются симметричными, поэтому достаточно вычислять элементы, находящиеся только выше (либо только ниже) главной диагонали.
являются симметричными, поэтому достаточно вычислять элементы, находящиеся только выше (либо только ниже) главной диагонали.
23.3.2 Алгоритм Данцига
Этот алгоритм отличается от алгоритма Флойда последовательностью выполнения действий. Перенумеруем все вершины графа от 1 до n целыми числами и обозначим через 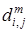 длину пройденного пути из
длину пройденного пути из 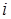 в
в 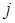 где в качестве промежуточных использованы первые m вершин графа. Матрица
где в качестве промежуточных использованы первые m вершин графа. Матрица 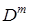 длин кратчайших путей имеет здесь размерность
длин кратчайших путей имеет здесь размерность 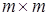 .
.
1. Каждая вычисленная матрица 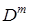 содержит на одну строку и столбец больше чем ее предшественница. Элементы матрицы не входящие в последнюю строку или столбец вычисляются так же, как и в алгоритме Флойда.
содержит на одну строку и столбец больше чем ее предшественница. Элементы матрицы не входящие в последнюю строку или столбец вычисляются так же, как и в алгоритме Флойда.
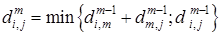 .
.
2. Кратчайший путь из вершины 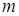 в
в 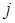 , в котором допускаются первые
, в котором допускаются первые 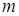 промежуточных вершин, должен иметь в своей первой части дугу из вершины
промежуточных вершин, должен иметь в своей первой части дугу из вершины 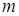 в некоторую вершину
в некоторую вершину  , a во второй – кратчайший путь из вершины
, a во второй – кратчайший путь из вершины  в
в 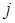 .
.
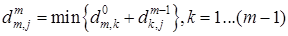 .
.
3. Кратчайший путь из вершины i в m, в котором допускается первых m промежуточных вершин. Имеет своей первой частью кратчайший путь из вершины 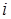 в некоторую промежуточную вершину
в некоторую промежуточную вершину  . А во второй – кратчайшую дугу из
. А во второй – кратчайшую дугу из  в
в 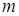 .
.
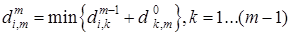 .
.
4. Диагональный элемент матрицы равен 0.
Алгоритм:
Перенумеровать вершины графа, определить матрицу 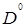 размером
размером 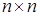 где
где  число вершин графа. Каждый элемент этой матрицы есть длина кратчайшей дуги от одной вершины до другой.
число вершин графа. Каждый элемент этой матрицы есть длина кратчайшей дуги от одной вершины до другой.
Для каждого m принимающего значения 1,2,3…N определить матрицу 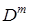 по формулам (2) – для строки
по формулам (2) – для строки 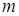 , (3) – для столбца
, (3) – для столбца 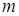 , (1) – для всех остальных элементов, кроме диагонального
, (1) – для всех остальных элементов, кроме диагонального 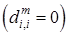 .
.
23.4 Транспортные сети и потоки
23.4.1 Основные определения транспортных сетей
Определение. Транспортной сетью называется пара 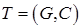 , где
, где  – взвешенный орграф, удовлетворяющий следующим условиям:
– взвешенный орграф, удовлетворяющий следующим условиям:
а) нет петель;
б) существует только одна вершина, не имеющая ни одного прообраза – это исток;
в) существует только одна вершина, не имеющая ни одного образа – это сток;
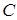 – функция пропускных способностей дуг, которая является положительной вещественной функцией, определенной на множестве дуг графа, т.е. каждой дуге
– функция пропускных способностей дуг, которая является положительной вещественной функцией, определенной на множестве дуг графа, т.е. каждой дуге  графа поставлено в соответствие положительное число
графа поставлено в соответствие положительное число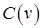 , называемое пропускной способностью дуги
, называемое пропускной способностью дуги 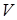 .
.
Определение.Вершина, не имеющая ни одного прообраза, называется входом сети или источником и обычно обозначается 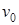 , а вершина, не имеющая ни одного образа, называется выходом сети или стоком и обозначается
, а вершина, не имеющая ни одного образа, называется выходом сети или стоком и обозначается 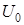 . В транспортной сети существует один исток и один сток. Случаи, когда имеется несколько источников или несколько стоков, могут быть сведены к рассматриваемому нами случаю введением обобщенных (фиктивных) источника и стока.
. В транспортной сети существует один исток и один сток. Случаи, когда имеется несколько источников или несколько стоков, могут быть сведены к рассматриваемому нами случаю введением обобщенных (фиктивных) источника и стока.
Определение. Потоком в транспортной сети  называется неотрицательная вещественная функция, определенная на множестве дуг, удовлетворяющая условиям:
называется неотрицательная вещественная функция, определенная на множестве дуг, удовлетворяющая условиям:
– ограниченности: поток по любой дуге сети не превосходит пропускной способности этой дуги;
– сохранения: суммарный поток, заходящий в любую вершину сети (кроме истока и стока) равен суммарному потоку, выходящему из этой вершины.
Определение.Дуга сети называется насыщенной, если поток по этой дуге равен пропускной способности этой дуги.
Определение.Поток по пути называется полным, если хотя бы одна дуга пути насыщена.
Определение.Как упоминалось выше, поток в сети – это функция, определенная на множестве дуг. Величиной потока называется сумма значений этой функции по всем выходным дугам сети (выходные дуги сети – это дуги, инцидентные стоку) .Понятия потока и величины потока в сети часто путают, однако между ними существует различие: поток – это функция, а величина потока – число.
Определение. Разрезом сети называется множество, которому принадлежит исток, и не принадлежит сток. Т.е. разрез – это минимальное (в смысле отношения включения) множество дуг, удаление которых “разрывает” все пути, соединяющие исток и сток.
Определение. Пропускной способностью разреза называется число, равное сумме пропускных способностей дуг этого разреза. Разрез называется минимальным, если имеет наименьшую пропускную способность.
Отыскание минимального разреза – одна из основных задач анализа транспортных сетей.
В силу конечности графа минимальный разрез может быть найден перебором всех разрезов, но этот путь, конечно, неприемлем для достаточно больших графов. Оказывается, что минимальный разрез можно отыскать при помощи максимального потока сети на основании теоремы Форда-Фалкерсона.
23.4.2 Теорема Форда-Фалкерсона. Алгоритм Форда-Фалкерсона
В любой транспортной сети величина любого максимального потока равна пропускной способности любого минимального разреза.
Известно конструктивное доказательство этой теоремы, на основании которого построен изложенный алгоритм.
Постановка задачи:найти максимальный поток в транспортной сети.
Алгоритм Форда-Фалкерсона:
1. Перенумеровать все вершины сети произвольным образом, кроме истока и стока.
2. Задать некоторый начальный поток в сети (например, нулевой).
3. Вершинам сети присвоить целочисленные метки, а дугам – знаки “+” и “–” по следующим правилам:
а) вершине-истоку присвоить метку 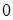 ;
;
б) находим непомеченную вершину 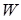 , смежную помеченной вершине
, смежную помеченной вершине 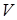 . Если поток по соединяющей вершины
. Если поток по соединяющей вершины 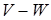 дуге меньше пропускной способности этой дуги, то происходит помечивание, иначе переходим к рассмотрению следующей вершины. Если вершина
дуге меньше пропускной способности этой дуги, то происходит помечивание, иначе переходим к рассмотрению следующей вершины. Если вершина 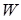 является образом помеченной вершины
является образом помеченной вершины 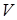 , то происходит прямое помечивание: вершина
, то происходит прямое помечивание: вершина 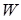 получает метку, равную номеру вершины
получает метку, равную номеру вершины 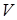 , соединяющая вершины
, соединяющая вершины 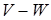 дуга получает метку “ + ” и мы переходим к рассмотрению следующей вершины. Если вершина W не имеет ни одного помеченного прообраза, то происходит обратное помечивание: вершина
дуга получает метку “ + ” и мы переходим к рассмотрению следующей вершины. Если вершина W не имеет ни одного помеченного прообраза, то происходит обратное помечивание: вершина 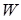 получает метку, равную номеру вершины
получает метку, равную номеру вершины 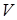 (являющейся в данном случае её образом), соединяющая вершины
(являющейся в данном случае её образом), соединяющая вершины 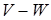 дуга получает метку “ – ” и мы переходим к рассмотрению следующей вершины. Процесс помечивания продолжается до тех пор, пока все удовлетворяющие этим условиям вершины не получат метку.
дуга получает метку “ – ” и мы переходим к рассмотрению следующей вершины. Процесс помечивания продолжается до тех пор, пока все удовлетворяющие этим условиям вершины не получат метку.
4. Если в результате процедуры помечивания вершина-сток метки не получила, то текущий поток – максимальный, задача решена. В противном случае, перейти к пункту 5.
5. Рассмотреть последовательность вершин 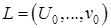 , метка каждой из которых равна номеру следующей за ней вершины, и множество дуг
, метка каждой из которых равна номеру следующей за ней вершины, и множество дуг  , соединяющих соседние вершины из
, соединяющих соседние вершины из 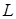 .
.
Построить новый поток по схеме: если дуга принадлежит множеству  и имеет знак “ + ”, то новый поток по этой дуге = старый поток по этой дуге +
и имеет знак “ + ”, то новый поток по этой дуге = старый поток по этой дуге + 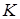 .
.
Если дуга принадлежит множеству  и имеет знак “–”, то новый поток по этой дуге = старый поток по этой дуге –
и имеет знак “–”, то новый поток по этой дуге = старый поток по этой дуге – 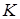 .
.
Если дуга не принадлежит множеству  , то новый поток по дуге = старый поток по этой дуге.
, то новый поток по дуге = старый поток по этой дуге.
Схема нахождения К: 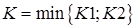 :
:
– для нахождения 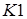 рассматриваются все дуги, принадлежащие множеству
рассматриваются все дуги, принадлежащие множеству  и имеющие знак “ + ” и для каждой такой дуги вычисляется разность между пропускной способностью дуги и потоком по этой дуге. Затем из этих значений разностей выбирается минимальное значение и присваивается
и имеющие знак “ + ” и для каждой такой дуги вычисляется разность между пропускной способностью дуги и потоком по этой дуге. Затем из этих значений разностей выбирается минимальное значение и присваивается 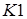 .
.
– для нахождения 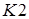 рассматриваются все дуги, принадлежащие множеству
рассматриваются все дуги, принадлежащие множеству  и имеющие знак “ – ”. Затем из этих дуг выбирается дуга с минимальным потоком и значение потока по этой дуге присваивается
и имеющие знак “ – ”. Затем из этих дуг выбирается дуга с минимальным потоком и значение потока по этой дуге присваивается 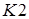 .
.
Далее следует перейти к пункту 3.
Алгоритм Форда-Фалкерсона используется при решении многих практических задач. Одна из них – Задача об источниках и потребителях.
Пример. Найти максимальный поток для транспортной сети  :
:
