Алгоритмический этап проект-я цифрового автомата

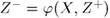Производится построение системных выходных ф-ий Y=f(X, Z⁺) и сис-мы ф-ий возбуждения
На этом этапе заданный автоматный оператор A оформляется в виде алгоритма, исходя из уст треб-ий. Поиск опт алг-ма по A можно представить в виде дерева, каждый лист которого соответствует опредленному алг-му, а кол-во таких листов заранее не известно. Проектирование автоматного опер-ра заключается в построении автоматного отображения по словесному описанию(цель проектирования, назначение автомата, свойства поведения упр-го объекта)

Автоматное отображение обычно задается графом переходов (каждая вершина взаимно однозначно соответствует внутр состоянию автомата, если из g_i переходит в g_j то соотв вершины u_i u_j соед-ся дугой (u_i u_j) взвешенной парой векторов (X,Y) по к-м переход и осуществляется
При преобразовании неформальной инф-ции в формальную сис-му используется принцип аналогий. Формально мб основан на прим-ии грамматик, в к-х правила подстановки формализуют данные св-ва упр-го объекта.
В рез-те применения грамматик порождаются композиции графов переходов, соотв описанию. Часто двухуровневые: 1 ур – графы пер-в, реакция к-х – воздействие на объект, 2 ур – граф пер-в, реакция к-го – возбуждение инициальных вершин графов 1-го уровня
Зная опер авт-т и алгоритм, можно составить временную диаграмму функционирования управляющего автомата – алгоритм выполнения операций в терминах управляющих точек – микроопераций. Но вр диаграмма еще не дает апп. отображения , тк 1 знач вх вектора(опр-т вып-ую опер-ию) соотв-т нексколько значений вых вектора(микрокоманд). Необходимо ввести в автомат память, при этом задать заведомо достаточный объем памяти. Тогда совокупность вх вектора и сост-ия памяти однозначно опр-т микрокоманду.

32. Абстрактное проект-ие автоматов.
Математической моделью устройства с памятью является абстрактный автомат, который представляет собой совокупность пяти конечных множеств:

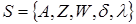
где A={a0, a1, .aM} - множество состояний автомата;={Z1, Z2, .ZF} - множество входных сигналов;={W1, W2, .WC} - множество выходных сигналов;
сигма- функция переходов, обеспечивающая выработку последующего состояния as автомата в зависимости от существующего состояния aM и входного воздействия Zf;
лямбда - функция выходов, обеспечивающая выработку выходного сигнала автомата в зависимости от его состояния aM и входного сигнала Zf.
Абстрактный автомат имеет один входной и один выходной каналы, и каждой букве входного алфавита Z ставит в соответствие букву или слово выходного алфавита W.
Автомат называется синхронным, если он описывается a(t) и W(t) как автомат Мили. Автомат называется асинхронным, если его функция переходов описывается как у автомата Мура.
В синхронном автомате осуществляется синхронизация внешних и внутренних сигналов, в то время как в асинхронном этого нет, и для представления последовательности одинаковых букв вводится какая-либо разделяющая их буква, не несущая информации.