Эквиваленция (двойная импликация)

Операция эквиваленции соответствует построению "тогда и только тогда" и обозначается символом "ó" или "≡". Эквиваленция определяется как сложное высказывание вида . Построим таблицу соответствия (табл.3.5) при помощи таблиц для импликаций и .

Таблица 3.5
х1	х2

Исходя из таблицы соответствия, эквиваленцию (х₁óx₂) можно также определить как высказывание, которое истинно тогда и только тогда, когда высказывания x₁ и х₂ либо оба истинны, либо оба ложны.

Так же как и импликация, операция эквиваленции очень часто применяется при формулировке различных теорем. В отличие от импликации, эквиваленция определяет необходимые и достаточные условия.

Вопросы и задания

3.14. Составьте сложное высказывание с использованием операции эквиваленции из следующих простых высказываний: "Сумма квадратов двух сторон треугольника равна квадрату третьей стороны", "Треугольник прямоугольный". Проверьте результат по таблице соответствия.

3.15. С использованием операции эквиваленции сформулируйте сложное высказывание, описывающее срабатывание предохранителя в электрической цепи.

3.16. Приведите пример теоремы, при формулировке которой используется операция эквиваленции.

Принципы доказательства тождеств. Таблица операций с двумя логическими переменными

Возникает вопрос: как доказать, что выражение действительно является тождеством? Есть два пути:

1. Доказательство на основе таблицы соответствия. Для обеих частей предполагаемого тождество строятся таблицы соответствия. Если эти таблицы получаются одинаковыми (т.е. для каждого набора значений аргументов значения левой и правой части выражения совпадают), то тождество верно.

2. Доказательство путем последовательных тождественных преобразований. Последовательно преобразуя левую и правую части, необходимо привести их к одинаковому виду. Правила, по которым производятся тождественные преобразования будут рассмотрены в гл.5.

Всего существует 16 операций с двумя логическими (булевыми) переменными (табл.3.6).

Очевидно, что одни операции могут быть выражены через другие. Например, дизъюнкция может быть выражена через конъюнкцию и отрицание:

Существуют две операции (стрелка Пирса и штрих Шеффера), через любую из которых может быть выражена любая другая операция. Например:

Множество всех булевых функций вместе с операциями отрицания, конъюнкции и дизъюнкции образуют булеву алгебру.

Таблица 3.6
x1					Варианты обозначения	Названия	Чтение
x2
y0						Константа 0 (тождественный нуль, всегда ложно)	Любое 0
y1						Конъюнкция (логическое "и", произведение, пересечение, совпадение)	x1 и x2 (и x1 и x2)
y2						Отрицание импликации (совпадение с запретом, антисовпадение, запрет)	x1, но не x2
y3						Повторение (утверждение, доминация) первого аргумента	Как x1
y4						Отрицание обратной импликации (обратное антисовпадение)	Не x1, но x2
y5						Повторение (утверждение, доминация) второго аргумента	Как x2
y6						Сумма по модулю 2 (неравнознач-ность, антиэквивалентность, исключающее "или")	x1 не как x2 (или x1 или x2)
y7						Дизъюнкция (разделение, логическая сумма, сборка, логическое "или")	x1 или x2 (x1 или хотя бы x2)
y8						Стрелка Пирса (функция Вебба, отрицание дизъюнкции, логическое "не–или")	Ни x1, ни x2
y9						Эквиваленция (равнозначность, эквивалентность, взаимозависимость)	x1 как x2 (x1, если и только если x2)
y10						Отрицание (инверсия) второго аргумента (дополнение к первой переменной)	Не x2
y11						Обратная импликация (обратное разделение с запретом, обратная селекция)	Если x2, то x1 (x1 или не x2)
y12						Отрицание (инверсия) первого аргумента (дополнение ко второй переменной)	Не x1
y13						Импликация (разделение с запретом, следование, селекция)	Если x1, то x2 (не x2 или x1)
y14						Штрих Шеффера (отрицание конъюнкции, несовместность, логическое "не–и")	Не x2 или не x1
y15						Константа 1 (тождественная единица, всегда истинно)	Любое 1

Вопросы и задания

3.17. При помощи таблиц соответствия проверьте, какие из следующих выражений являются верными тождествами:

а) ;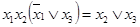

б) ;

в) ;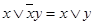

г) .