КИХ-фильтр задается уравнением

ПРОЦЕССОРЫ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ

6.1. ПРИНЦИПЫ ОРГАНИЗАЦИИ ПРОЦЕССОРОВ ОБРАБОТКИ

СИГНАЛОВ

ПРИНЦИПЫ ОБРАБОТКИ СИГНАЛОВ В ЦИФРОВЫХ

СИСТЕМАХ

Архитектура DSP определяется несколькими базовыми операциями, которые используются в алгоритмах ЦОС.

Для выделения таких операций проведем функциональный анализ основных направлений ЦОС, к которым относятся цифровая фильтрация и спектральный анализ.

Цифровая фильтрация. В области цифровой фильтрации разработчик систем ЦОС имеет дело с реализацией КИХ- и БИХ-фильтров (с конечной и бесконечной импульсными характеристиками соответственно).

Оба класса фильтров относятся к классу линейных систем с постоянными параметрами (ЛСПП), в которых входная х_n и выходная у_nпоследовательности связаны отношениями типа свертки. Если обозначить через h_k отклик системы на единичный импульс (импульсную характеристику ЛСПП), то получим свертку вида

где х_n, у_n - отсчеты входного и выходного сигналов; х_n-k - входной отсчет, задержанный на k интервалов дискретизации.

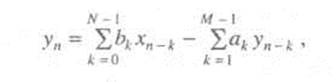В КИХ-фильтре отсчет выходного сигнала определяется только значениями входного сигнала, а в БИХ-фильтре - значениями входного и выходного сигналов. Это хорошо видно из линейных разностных уравнений с постоянными коэффициентами, которыми описывается данный класс дискретных систем. В общем виде разностное уравнение, описывающее БИХ-фильтр, имеет вид

где N, М— постоянные целые числа; b_k, a_k - постоянные коэффициенты, описывающие конкретную систему; х_n, у_n - отсчеты входного и выходного сигналов.

КИХ-фильтр задается уравнением

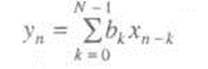или иначе

y_n =b₀х_n,+b₁х_n-1+b₂х_n-2+ ... +b_nx_n-N+1

Таким образом, для построения систем цифровой фильтрации требуется эффективная реализация соотношения типа дискретной свертки, которая раскладывается на операции умножения и накапливающего суммирования, а также операции задержки.

Спектральный анализ. В области спектрального (или гармонического анализа) используются прямое и обратное дискретное преобразование Фурье (ДПФ), а также рациональный способ реализации дискретного преобразования Фурье - быстрое преобразование Фурье (БПФ).

Спектральный анализ основан на известных методах представления данной функции при помощи других функций, которые называются базовыми и свойства которых считаются известными.

Если входная последовательность х^р_п периодична, то ее можно представить рядом Фурье

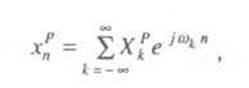где х^p_k- амплитуда гармоники; е^{jωk n} =cosω_kn + jsinaω_k n- комплексная переменная;

ω_к = 2πк / N - частота спектральной составляющей (гармоники).

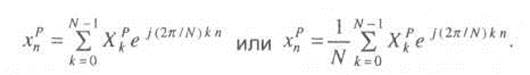Учитывая, что е^{jωk n} периодична, ряд Фурье записывается в виде

Данное выражение, описывающее Фурье-образ функции, называется обратным преобразованием.

Для вычисления коэффициентов ряда используется следующее выражение для ДПФ

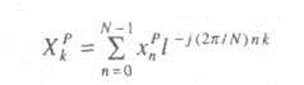или в более компактной форме

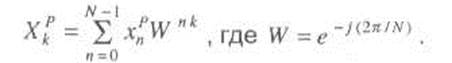Анализ данного выражения показывает, что основными операциями при вычислении выражения являются операции комплексного умножения и суммирования. Трудоемкость прямого вычисления данного выражения велика и возрастает с ростом N.

Для упрощения вычисления ДПФ исходную N/-точечную последовательность разбивают на две более короткие, для которых отдельно вычисляется БПФ, а результаты далее комбинируются для получения окончательного БПФ всей последовательности. Причем деление последовательности может быть многократным.

Если последовательность разбивается на две: одна с четными, а другая с нечетными номерами, то БПФ реализуется с прореживанием по времени (входная последовательность прореживается на каждом этапе разбиения). Если в первой последовательности берутся первые N/2 отсчеты (0,..., N/2),a во второй - вторые N/2 отсчетов, N/2+ 1,..., N). то БПФ реализуется с прореживанием по частоте.

Оценить сложность алгоритмов БПФ, а также их особенности можно из анализа вычислительной схемы, в основе которой лежит операция над двумя точками последовательности.

Элементарная операция (операция «бабочка»), которая определяет двухточечное преобразование, сводится к вычислению выражений:

x = A + BW^K_N;

y = A - BW^K_N,

где А, В - входные значения; W^K_N- коэффициент.

Для получения выходной последовательности в естественном порядке необходимо определенным образом переставить входную последовательность. Перестановка входных элементов состоит в образовании двоичных номеров выходной последовательности путем добавления единицы к старшему разряду с распространением переноса в сторону младших разрядов (вправо). Такая адресация получила название бит-реверсивной.

Вычисление коэффициента W^K_N=cos[(2π /N)К}-jsin[(2n/N)K] можно осуществлять следующим образом:

• используя подпрограммы или таблицы синуса и косинуса;

• прямым табличным способом (выборкой готовых значений из таблицы);

• используя рекуррентную формулу

W^K_N= (W^K-_N^L) W^L_N при W⁰_N=1;

•таблично-алгоритмическим способом, так как на последующих этапах

коэффициенты повторяются.

При использовании алгоритма БПФ с прореживанием по частоте требуется перестановка элементов выходной последовательности, а базовая операция «бабочка» сводится к вычислению выражений:

х = А+В,

y = (A-B) W^K_N,

Для получения амплитуд и фаз составляющих спектра (гармоник) необходимо также вычислить следующие выражения:

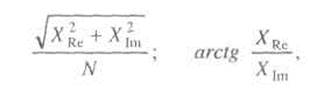где X_Re., Х_Im - вещественная и мнимая части комплексных коэффициентов.

В гомоморфной обработке сигналов дополнительно требуется вычисление функций

log₂ х и 2^х.