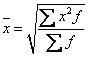Методика определения средней арифметической величины

Средняя арифметическая величина выборки

характеризует средний уровень значений изучаемой случайной величины в наблюдавшихся случаях и вычисляется путем деления суммы отдельных величин исследуемого признака на общее число наблюдений:

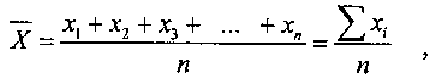
где 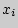- значение конкретного показателя,

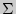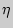- нак суммирования,

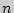- число показателей (случаев).

24 Математические свойства средней арифметической.

Понятие средней арифметической

Виды средних величин различаются прежде всего тем, какое свойство, какой параметрисходной варьирующей массы индивидуальных значений признака должен быть сохраненнеизменным.

Средней арифметической величиной называется такое среднее значение признака, привычислении которого общий объем признака в совокупности сохраняется неизменным.

Иначе можно сказать, что средняя арифметическая величина -среднее слагаемое. При еевычислении общий объем признака мысленно распределяется поровну между всеми единицамисовокупности. Например, средняя заработная плата или средний доход работниковпредприятия - это такая сумма денег, которая приходилась бы на каждого работника, если бывесь фонд оплаты труда (или все доходы, направленные на личное потребление) былраспределен между работниками поровну.

Исходя из определения, формула средней арифметической величины имеет вид:

Средняя арифметическая

,

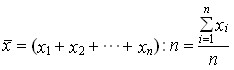где х? - средняя величина;

п – численность совокупности.

25. Использование свойств средней арифметической при расчете способом "моментов".

Если данные представлены в виде ряда распределения, то вопрос о выборе формы средней решается однозначно — средняя арифметическая. Этот вывод можно сделать, если вспомнить о том, что ряд распределения есть не что иное как распределение значений варьирующего признака по частоте их появлений в совокупности.

Ряды распределения довольно часто встречаются в статистической практике. При этом варианта может быть задана в виде интервалов, если признак непрерывный, или в виде индивидуальных значений, если ряд дискретный. Для дискретных рядов расчет осуществляется по вышеприведенной формуле средней арифметической взвешенной. Для интервального ряда распределения задача расчета средней величины решается следующим образом. Предполагаем, что в пределах интервала значения признаков располагаются равномерно, поэтому середина интервала будет величиной, характеризующей весь интервал, то есть наиболее типичным для него значением. Данное предположение не всегда выполняется поэтому, чем меньше величина интервала, тем точнее его середина будет характеризовать весь интервал. Далее используется обычная формула средней, только значения варианты будут приравниваться к середине соответствующего интервала. Расчет средней по непрерывному признаку (представленному в виде интервалов) был рассмотрен в примере 2.

В том случае, если ряд распределения имеет равные интервалы, расчет средней может быть существенно упрощен. Упрощенные способы расчета средней арифметической базируются на знании ее свойств.

Свойства средней арифметической:

• если все веса (f) увеличить или уменьшить в одинаковое число раз (d), то величина средней не изменится:

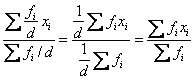
• если каждую варианту (х) увеличить или уменьшить на одну и ту же величину, то средняя увеличится или уменьшится на эту же величину:

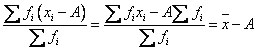
• если каждую варианту (х) увеличить или уменьшить в одно и то же число раз (h), то средняя увеличится или уменьшится в то же число раз.

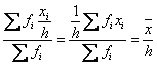
• сумма отклонений вариант от средней, взвешенных их частотами равна нулю:

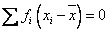
Перечисленные свойства средней арифметической используются при расчете средней способом моментов или способом отсчета от условного начала (0). При использовании этого способа последовательно осуществляются следующие операции:

• определяются срединные значения интервалов как полусумма начала и конца интервалов;
• варианта (серединное значение интервала) с наибольшей частотой принимается за условное начало отсчета (А);
• рассчитывается момент 1-го порядка:

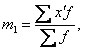
где

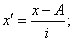i	— величина интервала.

Средняя рассчитывается по формуле:

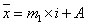
Наряду со средней арифметической и средней гармонической, к другим степенным средним относится средняя геометрическая. В статистике она используется для осреднения темпов роста, коэффициентов динамики:

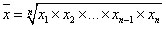
Средняя квадратическая используется при расчете показателей вариации, в частности — среднеквадратического отклонения, при исчислении средних ошибок выборки:

...
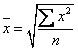