Математические действия с высказываниями
Приложение к Части I
Теперь, когда вы уже прошли кое‑что и из математической логики, и из теории множеств, я думаю, что вам будет небезынтересно узнать, что есть кое-что, связывающее эти два раздела математики.
На Лекции №1 вы узнали, что объектом математической логики являются высказывания - утверждения о которых можно сказать, истинны они или ложны, и предикаты - утверждения, зависящие от переменной, которые при подстановке одних значений переменной превращаются в истинное высказывание, а для остальных значений переменной являются ложными высказываниями.
Рассмотрим, например, такой предикат: 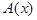 = “Квадратный корень из числа
= “Квадратный корень из числа 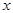 больше 9”. При одних значениях переменной
больше 9”. При одних значениях переменной 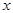 - например, при
- например, при 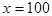 -
- 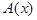 превращается в истинное высказывание, а при других - например, при
превращается в истинное высказывание, а при других - например, при 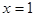 - в ложное высказывание. Это типичный предикат. Слово “предикат” по‑латыни означает просто “сказуемое”. Действительно, предикат - это как бы сказуемое без подлежащего: мы говорим, что какое‑то число больше 9, но какое именно - не определено. Предикат становится высказыванием, т.е. истинным либо ложным утверждением, лишь тогда, когда мы подставляем в него конкретное значение переменной.
- в ложное высказывание. Это типичный предикат. Слово “предикат” по‑латыни означает просто “сказуемое”. Действительно, предикат - это как бы сказуемое без подлежащего: мы говорим, что какое‑то число больше 9, но какое именно - не определено. Предикат становится высказыванием, т.е. истинным либо ложным утверждением, лишь тогда, когда мы подставляем в него конкретное значение переменной.
Переменная 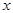 может принимать любые значения из некоторого множества
может принимать любые значения из некоторого множества 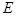 . Подмножество множества
. Подмножество множества 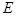 , состоящее из тех значений
, состоящее из тех значений 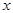 , для которых
, для которых 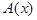 истинно, называется множеством истинности предиката
истинно, называется множеством истинности предиката 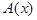 . Мы будем обозначать множество истинности той же буквой, что и предикат, -
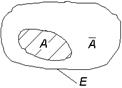
. Мы будем обозначать множество истинности той же буквой, что и предикат, - 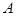 (см. рис.1,а). Тогда для оставшейся части множества
(см. рис.1,а). Тогда для оставшейся части множества 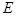 - для множества
- для множества 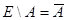 - предикат
- предикат 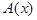 является ложным, следовательно, отрицание предиката -
является ложным, следовательно, отрицание предиката - 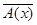 - является истинным. Вывод: дополнение множества
- является истинным. Вывод: дополнение множества 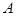 -
- 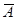 - является множеством истинности отрицания предиката
- является множеством истинности отрицания предиката 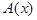 .
.
Например, в предикате 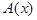 = “Квадратный корень из числа
= “Квадратный корень из числа 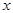 больше 9” переменная
больше 9” переменная 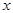 не может быть отрицательным числом, поэтому этот предикат определен на множестве
не может быть отрицательным числом, поэтому этот предикат определен на множестве 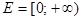 . Множеством истинности этого предиката, очевидно, является множество
. Множеством истинности этого предиката, очевидно, является множество 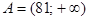 . Дополнение этого множества до множества
. Дополнение этого множества до множества 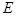 -
- 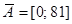 - является множеством истинности для отрицания данного предиката - для предиката
- является множеством истинности для отрицания данного предиката - для предиката 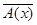 = “Квадратный корень из числа
= “Квадратный корень из числа 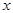 меньше либо равен 9”.
меньше либо равен 9”.
 а) а) | 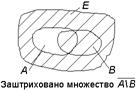 б) б) |
Рис. 1
Теперь становится очевидной аналогия между множествами и предикатами. Вместо того, чтобы работать с предикатами, мы можем работать с множествами их истинности. Математическая логика переводится на язык теории множеств.
Найдем множество истинности импликации 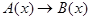 . (Напомню, что так называется высказывание вида: “Если
. (Напомню, что так называется высказывание вида: “Если 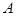 истинно, то и
истинно, то и 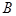 тоже истинно”; здесь высказывание
тоже истинно”; здесь высказывание 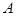 называется условием импликации, а высказывание
называется условием импликации, а высказывание 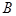 - ее заключением.) Предполагаем, что нам известны множества истинности
- ее заключением.) Предполагаем, что нам известны множества истинности 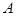 и
и 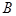 - подмножества некоторого основного множества
- подмножества некоторого основного множества 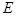 . Тогда искомое множество - это множество всех
. Тогда искомое множество - это множество всех 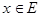 , кроме тех, для которых условие
, кроме тех, для которых условие 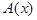 истинно, а заключение
истинно, а заключение 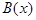 ложно. Таким образом, это множество
ложно. Таким образом, это множество 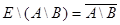 (см. рис.1,б).
(см. рис.1,б).
Теперь становится очевидной аналогия между множествами и предикатами. Вместо того, чтобы работать с предикатами, мы можем работать с множествами их истинности. Математическая логика переводится на язык теории множеств.
Введем два новых математических действия с высказываниями и предикатами - дизъюнкцию и конъюнкцию.
1) Дизъюнкция (сумма) высказываний 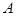 и
и 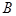 - это высказывание вида: “Или
- это высказывание вида: “Или 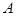 , или
, или 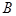 является истинным высказыванием”, “Хотя бы одно из высказываний
является истинным высказыванием”, “Хотя бы одно из высказываний 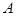 ,
, 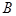 истинно”. Дизъюнкция обозначается просто
истинно”. Дизъюнкция обозначается просто 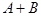 .
. 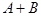 считается истинной во всех случаях, кроме случая, когда
считается истинной во всех случаях, кроме случая, когда 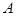 и
и 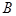 одновременно ложны.
одновременно ложны.
2) Конъюнкция (произведение) высказываний 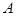 и
и 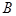 - высказывание вида “Оба высказывания
- высказывание вида “Оба высказывания 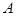 и
и 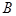 истинны одновременно”. Очевидно, такое высказывание будет истинным в единственном случае - когда действительно и
истинны одновременно”. Очевидно, такое высказывание будет истинным в единственном случае - когда действительно и 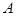 , и
, и 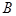 истинны одновременно. Конъюнкция обозначается
истинны одновременно. Конъюнкция обозначается 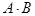 .
.
Итак, теперь мы знаем четыре математических действия с высказываниями и предикатами: отрицание, импликацию, дизъюнкцию и конъюнкцию. Чтобы закрепить это новое знание, составим таблицу истинности этих операций, а заодно укажем их множества истинности:
| Высказывание | А | В | 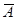 | 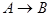 | 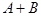 | 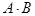 |
| Вариант 1 | И | И | Л | И | И | И |
| Вариант 2 | И | Л | Л | Л | И | Л |
| Вариант 3 | Л | И | И | И | И | Л |
| Вариант 4 | Л | Л | И | И | Л | Л |
| Множество истинности | А | В | 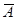 | 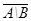 | 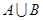 | 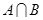 |
В дальнейшем мы можем поставить в соответствие каждому действию с предикатами его множество истинности и работать не с предикатами, а с множествами.
Аналогия между операциями над высказываниями и операциями над множествами - полная. Поэтому операции над высказываниями и предикатами обладают теми же свойствами, что и операции над множествами:
1) переместительные свойства: 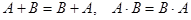 ,
,
2) сочетательные свойства: 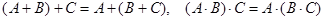 ,
,
3) распределительные свойства: 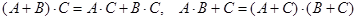 ,
,
4) законы де Моргана: 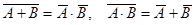 ,
,
5) свойство импликации: 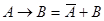 .
.
Последнее свойство не встречалось вам в теории множеств. Но, если перевести его на язык теории множеств, оно будет справедливо и для множеств: 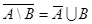 . Вы можете доказать это свойство самостоятельно - с помощью метода диаграмм. С точки зрения логики, это свойство имеет следующий смысл: высказывания “Если
. Вы можете доказать это свойство самостоятельно - с помощью метода диаграмм. С точки зрения логики, это свойство имеет следующий смысл: высказывания “Если 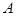 истинно, то и
истинно, то и 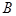 тоже истинно” и “Или
тоже истинно” и “Или 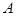 ложно, или
ложно, или 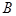 истинно, или выполняется и то, и другое” равносильны - они истинны либо ложны одновременно; в ходе логических рассуждений можно спокойно заменять одно высказывание на другое.
истинно, или выполняется и то, и другое” равносильны - они истинны либо ложны одновременно; в ходе логических рассуждений можно спокойно заменять одно высказывание на другое.
А теперь - примеры использования этих свойств.
Пример 1. При каком условии истинно высказывание 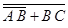 ?
?
Эту задачу можно решить двумя способами.
1‑й способ. Составим таблицу истинности для данного высказывания, рассмотрев всевозможные варианты истинности либо ложности высказываний 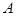 ,
, 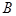 ,
, 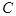 :
:
| А | В | С | А В | 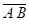 | В С | 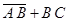 | 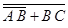 |
| И | И | И | И | Л | И | И | Л |
| И | Л | И | Л | И | Л | И | Л |
| И | И | Л | И | Л | Л | Л | И |
| И | Л | Л | Л | И | Л | И | Л |
| Л | И | И | Л | И | И | И | Л |
| Л | Л | И | Л | И | Л | И | Л |
| Л | И | Л | Л | И | Л | И | Л |
| Л | Л | Л | Л | И | Л | И | Л |
Ответ: данное высказывание истинно, только если 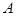 и
и 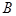 истинны, а
истинны, а 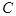 ложно.
ложно.
2‑й способ. Упростим выражение 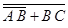 , пользуясь свойствами математических операций над высказываниями:
, пользуясь свойствами математических операций над высказываниями:
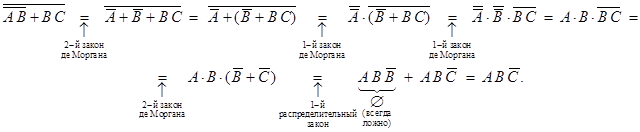
Мы получили тот же результат: высказывания 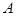 и
и 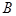 должны быть истинны, а
должны быть истинны, а 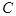 ложно. Согласитесь, что этот способ и быстрее, и изящнее.
ложно. Согласитесь, что этот способ и быстрее, и изящнее.
Пример 2. Ученикам объявили: “В понедельник будет 5 уроков, среди них - один урок физики и один - математики, причем, если на первом уроке математики не будет, то физика будет на втором уроке; если третий урок - не математика, то четвертый - физика; а если математика будет на первом уроке, то физика - на пятом”. Определить, на каком уроке будет физика и на каком - математика.
Решение. Переведем задачу на язык математической логики. Все 3 условия - это импликации вида “если …, то …”. Представим их как предикаты. На каком множестве они определены? Нас интересует номер урока математики 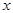 и номер урока физики
и номер урока физики 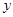 , т.е. пара чисел
, т.е. пара чисел 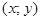 . При этом
. При этом 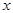 и
и 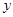 могут меняться от 1 до 5 и никогда не может быть
могут меняться от 1 до 5 и никогда не может быть 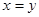 . Множество
. Множество 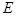 и есть множество таких пар чисел. Оно состоит из 20 элементов (действительно, если
и есть множество таких пар чисел. Оно состоит из 20 элементов (действительно, если 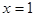 , то
, то 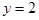 , 3, 4 или 5; если
, 3, 4 или 5; если 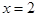 , то
, то 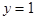 , 3, 4 или 5, и т.п., т.е. каждому
, 3, 4 или 5, и т.п., т.е. каждому 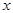 соответствует 4 варианта
соответствует 4 варианта 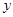 . Но
. Но 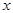 может принимать 5 различных значений - от 1 до 5; следовательно, всего может быть
может принимать 5 различных значений - от 1 до 5; следовательно, всего может быть 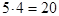 пар
пар 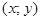 .
.
Примитивный способ решения этой задачи: перебрать все 20 пар (не так уж и много) и выяснить, какая из них удовлетворяет всем трем требованиям.
С помощью математической логики: выпишем множества истинности всех трех импликаций. Нас интересует случай, когда все эти три импликации истинны одновременно, т.е. пересечение множеств истинности этих импликаций.
Пусть 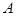 - множество истинности 1‑й импликации - все случаи, когда на первом уроке математики нет и второй урок - физика, а также все случаи, когда первый урок математика. Следовательно,
- множество истинности 1‑й импликации - все случаи, когда на первом уроке математики нет и второй урок - физика, а также все случаи, когда первый урок математика. Следовательно,
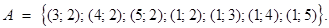
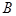 - множество истинности 2‑й импликации:
- множество истинности 2‑й импликации:
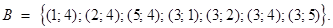
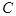 - множество истинности 2‑й импликации:
- множество истинности 2‑й импликации:
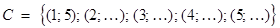
(… - любое значение 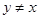 ).
).
Теперь найдем 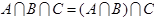 . Но
. Но 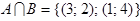 . Тогда
. Тогда 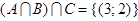 .
.
Ответ: математика будет на третьем уроке, физика - на втором.
Ну, эту задачу вы еще могли решить, не пользуясь математической логикой. А вот следующую - вряд ли.
Пример 3. “Вернувшись домой, комиссар Мегрэ позвонил в полицейский участок, чтобы выяснить, как продвигается расследование убийства. Его помощники сообщили ему, что они узнали. Инспектор Торранс установил, что если Франсуа был пьян, то либо Этьен убийца, либо Франсуа лжет. Инспектор Жуссье считает, что или Этьен убийца, или Франсуа не был пьян и убийство произошло после полуночи. Инспектор Люка выяснил, что если убийство произошло после полуночи, то либо Этьен убийца, либо Франсуа лжет. “Отлично. Этого достаточно”, - сказал Мегрэ. Он знал, что трезвый Франсуа никогда не лжет. Теперь он знал все.”
Итак, кто же убийца?
Переводим все на язык математической логики.
Высказывание 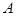 : “Франсуа был пьян”.
: “Франсуа был пьян”.
Высказывание 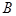 : “Этьен убийца”.
: “Этьен убийца”.
Высказывание 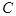 : “Франсуа лжет”.
: “Франсуа лжет”.
Высказывание 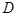 : “Убийство произошло после полуночи”.
: “Убийство произошло после полуночи”.
Тогда утверждение инспектора Торранса можно записать в следующем виде: 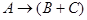 ; утверждение Жуссье:
; утверждение Жуссье: 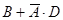 ; утверждение Люка:
; утверждение Люка: 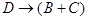 .
.
Но эти три высказывания должны быть истинны одновременно. Значит, их произведение -
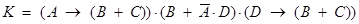
- истинное высказывание.
Упростим 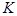 :
:
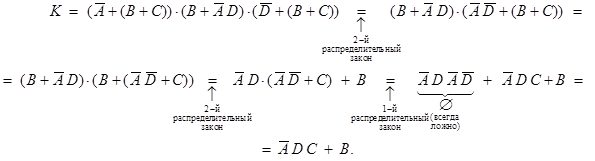

Итак, или истинно 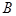 , или истинно
, или истинно 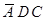 . Но
. Но 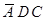 = “Франсуа был трезв, и убийство произошло после полуночи, и Франсуа лжет”. А Мегрэ знал, что трезвый Франсуа никогда не лжет! Значит,
= “Франсуа был трезв, и убийство произошло после полуночи, и Франсуа лжет”. А Мегрэ знал, что трезвый Франсуа никогда не лжет! Значит, 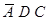 ложно. Значит истинно
ложно. Значит истинно 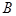 ,т.е. убийца - Этьен!
,т.е. убийца - Этьен!
Представьте, как бы вы решали эту задачу без математической логики!
На этом мы заканчиваем наше краткое знакомство с математической логикой и “наивной” теорией множеств.
