II. Элементы теории множеств.
Программа курса
«МАТЕМАТИЧЕСКАЯ ЛОГИКА»
для студентов 1-2 курсов ММФ НГУ
Программу составил д.ф.-м.н., доцент С.В.Судоплатов
Семестр
I. Исчисления высказываний.
1. Формулы ИВ, лемма о начале формулы ИВ. (Ершов, Палютин [1, § 2], [2, § 1.2])
2. Теоремы о подформулах формул ИВ. ([1, § 2], [2, § 1.2])
3. Аксиомы и правила вывода ИВ. ([1, § 3], [2, § 1.3])
4. Доказательства и теоремы ИВ, равносильность линейного доказательства и доказательства в виде дерева. ([1, § 3], [2, § 1.3])
5. Допустимые правила вывода ИВ. ([1, § 3], [2, § 1.3])
6. Теорема о подстановке. ([1, § 4], [2, § 1.4])
7. Эквивалентность формул, основные эквивалентности ИВ. ([1, § 4], [2, §1.4])
8. Теорема о замене. ([1, § 4], [2, § 1.4])
9. Нормальные формы. ([1, § 5], [2, § 1.5])
10. Теорема о существовании д.н.ф. ([1, § 5], [2, § 1.5])
11. Теорема о существовании к.н.ф. ([1, § 5], [2, § 1.5])
12. Теорема о существовании совершенной д.н.ф. ([1, § 5], [2, § 1.5])
13. Теорема о существовании совершенной к.н.ф. ([1, § 5], [2, § 1.5])
14. Интерпретация формул ИВ, теорема о непротиворечивости ИВ. ([1, § 6], [2, § 1.6])
15. Главная интерпретация формул ИВ, теорема о тождественной истинности доказуемых секвенций. ([1, § 6], [2, § 1.6])
16. Теорема о функциональной полноте ИВ. ([1, § 6], [2, § 1.6])
17. Теорема о полноте ИВ. ([1, § 7], [2, § 1.7])
18. Теорема о независимости ИВ. ([1, § 7], [2, § 1.7])
19. Исчисление высказываний гильбертовского типа ( 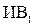 ).([1, § 8], [2, § 1.8])
).([1, § 8], [2, § 1.8])
20. Линейное доказательство в 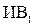 , вывод в
, вывод в 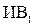 из множества гипотез. ([1, § 8], [2, § 1.8])
из множества гипотез. ([1, § 8], [2, § 1.8])
21. Теорема о дедукции в 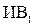 . ([1, § 8], [2, § 1.8])
. ([1, § 8], [2, § 1.8])
22. Теорема о равносильности ИВ и 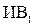 . ([1, § 8], [2, § 1.8])
. ([1, § 8], [2, § 1.8])
II. Элементы теории множеств.
1. Аксиомы объемности, пустого множества и пары. ([1, § 14], [2, § 2.6])
2. Аксиомы объединения, бесконечности и степени. ([1, § 14], [2, § 2.6])
3. Аксиома регулярности и ее следствия. ([1, § 14], [2, § 2.6])
4. Аксиомы подстановки и выбора. ([1, § 14], [2, § 2.6])
5. Упорядоченные наборы (определение и основное свойство). ([1, § 10], [2, § 2.1])
6. Отношения на множествах, композиция и инверсия бинарных отношений, их свойства. ([1, § 10], [2, § 2.1])
7. Типы бинарных отношений. ([1, § 10], [2, § 2.1])
8. Отношения эквивалентности и разбиения, связь между ними. ([1, § 10], [2, § 2.1])
9. Функции, отображения, их типы и свойства. ([1, § 10], [2, § 2.1])
10. Частично упорядоченные множества, особые элементы (максимальные, минимальные и т.п.) и их свойства. ([1, § 11], [2, § 2.2])
11. Решетки, булевы решетки, булевы алгебры, связь булевых решеток с основными свойствами теоретико-множественных операций. ([1, § 11], [2, § 2.2])
12. Фундированные частично упорядоченные множества, принцип трансфинитной индукции. ([1, § 11], [2, § 2.2])
13. Начальные отрезки, определение и свойства. ([2, § 2.2])
14. Принцип максимума. ([1, § 11], [2, § 2.2])
15. Линейно и вполне упорядоченные множества, принцип полного упорядочения. ([1, § 11], [2, § 2.2])
16. Характеризация вполне упорядоченных множеств. ([2, § 2.2])
17. Принцип кардинального упорядочения. ([2, § 2.2])
18. Теорема об изоморфизме вполне упорядоченных множеств. ([2, § 2.2])
19. Сравнение множеств по мощности, Теорема Кантора-Бернштейна. ([1, § 13], [2, § 2.4])
20. Теорема Кантора. ([1, § 13], [2, § 2.4])
21. Теорема о сравнимости множеств по мощности. ([1, § 13], [2, § 2.4])
22. Ординалы и их свойства. ([1, § 13], [2, § 2.5])
23. Теорема о представлении вполне упорядоченных множеств. ([1, § 13], [2, § 2.5])
24. Кардиналы и мощность множества. ([1, § 13], [2, § 2.5])
25. Натуральные числа и счетные множества. ([1, § 13], [2, § 2.5])
26. Конечные и бесконечные множества, их свойства. ([1, § 13], [2, § 2.5])
27. Теорема о квадрате бесконечного множества. ([1, § 13], [2, § 2.5])
28. Мощность множества слов данного алфавита. ([1, § 13], [2, § 2.5])
29. Теорема об утверждениях, эквивалентных аксиоме выбора. ([1, § 14], [2, § 2.6])
30. Доказательство теоремы Кантора-Бернштейна, не зависящее от аксиомы выбора. ([2, § 2.6])
Семестр
