Всюду далее скобки в формулах восстанавливайте самостоятельно.
1.Вычислите значения формул при указанных интерпретациях:
а)a ® b ® b ® a при a = b = 0 и при a = 1 , b = 0;
б)a ® (b ® b) ® a при a = b = 0 и при a = 1 , b = 0;
в)((aÚ 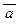 ) Ù (b ® c)) при a = b = c = 0 и при a = 1 , b = 1, с = 0;
) Ù (b ® c)) при a = b = c = 0 и при a = 1 , b = 1, с = 0;
г)a Ú 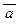 Ù b ® c при a = b = c = 0 и при a = 1 , b = 1, с = 0;
Ù b ® c при a = b = c = 0 и при a = 1 , b = 1, с = 0;
д)a Ù bÚ a ®  ® c « a Ú c при a = b = c = 0 и при a = 1, b = 0, c = 0;
® c « a Ú c при a = b = c = 0 и при a = 1, b = 0, c = 0;
е)(((a Ù b)Ú a)®((  ® c) « (a Ú c))) при a = b = c = 0 и при a = 1, b = 0, c = 0;
® c) « (a Ú c))) при a = b = c = 0 и при a = 1, b = 0, c = 0;
ж)  при a = b = c = 0 и при a = 1, b = 0, c = 0.
при a = b = c = 0 и при a = 1, b = 0, c = 0.
2.Для каждой из следующих формул укажите, достаточно ли приведённых сведений для определения значения формулы. Если достаточно, вычислите это значение. Если недостаточно, то покажите, что формула может принимать как значения 1 и 0:
а) 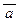 ® a, б) (a ® b) ® c, c = 1; в)
® a, б) (a ® b) ® c, c = 1; в)  «
« 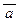 Ù
Ù  , b = 1; г) x Ú (y ® z), y = 1; д) x Ú (y ® z), z = 1; е) p Ù (q ® r) ® (p Ù q), r = 0; ж) x ®
, b = 1; г) x Ú (y ® z), y = 1; д) x Ú (y ® z), z = 1; е) p Ù (q ® r) ® (p Ù q), r = 0; ж) x ® , y = 0 = z.
, y = 0 = z.
3.Постройте таблицы истинности формул задания 1. Классифицируйте полученные формулы.
4.Дайте классификацию следующих формул, используя таблицы истинности:
а)  , б)x ® (y ® x), в)(a®
, б)x ® (y ® x), в)(a®  ) ® (b ® c) Ù
) ® (b ® c) Ù 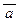 Ù
Ù 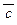 ,г)
,г)  , д)(a ® (b ® c)) ® ((a ® b) ® (a ® c)), е)(p ® q) Ù (q ®
, д)(a ® (b ® c)) ® ((a ® b) ® (a ® c)), е)(p ® q) Ù (q ®  ) Ù (r ® p), ж)a ® a Ú b, з)(x ® y) ® ((x ® (y ® z)) ® (x ® z)), и)x ® y ® x, к)
) Ù (r ® p), ж)a ® a Ú b, з)(x ® y) ® ((x ® (y ® z)) ® (x ® z)), и)x ® y ® x, к)  , л)x ® y Ù (x ® y), м) ((a ® b) ® ((a ® c) ® (a ® b Ù c))), н)(x ® z) ® ((y ® z) ® (x Ú y ® z)).
, л)x ® y Ù (x ® y), м) ((a ® b) ® ((a ® c) ® (a ® b Ù c))), н)(x ® z) ® ((y ® z) ® (x Ú y ® z)).
5.Докажите теорему об основных законах логики, построив таблицы истинности (см. приложение 1).
6.Не строя таблиц истинности, выясните, являются ли следующие формулы законами логики или противоречиями:
а)  , б)x « (
, б)x « (  ® x), в)
® x), в)  , г)u « (u ®
, г)u « (u ®  ), д)a Ú (a «
), д)a Ú (a « 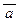 ),
),
е)(x Ú x) ® (x Ù x), ж)  , з)(p ® q) Ú (q ® p).
, з)(p ® q) Ú (q ® p).
7.Докажите, что если формулы A и A ® B являются законами логики, то B – тоже закон логики. Приведите пример таких тождественно истинных формул B и A ® B, для которых A – не тождественно истинна.
8.Верны ли следующие утверждения ?
а) если A Ú B и  Ú С – законы логики, то B Ú C – закон логики;
Ú С – законы логики, то B Ú C – закон логики;
б) если A Ú B, A ® C и B ® D – законы логики, то C Ú D – закон логики;
в)если A Ú B и  Ú С – законы логики, то B Ù C – закон логики;
Ú С – законы логики, то B Ù C – закон логики;
г) если  Ú B и
Ú B и  Ú
Ú  – законы логики, то A ®
– законы логики, то A ®  Ú
Ú  – закон логики;
– закон логики;
д) если A ® B и B ®  являются законами логики, то B – закон логики;
являются законами логики, то B – закон логики;
е)если A « B и B ® C – законы логики, то A ® C – закон логики;
ж) если  Ú B и
Ú B и  Ú
Ú  – законы логики, то A ®
– законы логики, то A ®  – закон логики.
– закон логики.
9.Докажите, что формула, полученная из переменных и их отрицаний с помощью дизъюнкциине может быть противоречием.
10.Докажите, что формула, полученная из конъюнкций переменных и их отрицаний с помощью дизъюнкциине может быть противоречием (переменная и её отрицание не могут одновременно входить в конъюнкцию).
11.Докажите, что формула, полученная из дизъюнкций переменных и их отрицаний с помощью конъюнкциине может быть тавтологией (переменная и её отрицание не могут одновременно входить в дизъюнкцию).
12.Приведите пример закона логики, в котором, используется только а) импликация, б) эквивалентность. Какова наименьшая длина такой формулы ?
13.Существует ли закон логики, в котором используются только а) конъюнкция, б) дизъюнкция, в) конъюнкция и дизъюнкция.
14.Существует ли противоречие, в котором используется только а) импликация, б) эквивалентность, в) конъюнкция, дизъюнкция и импликация, г) конъюнкция, дизъюнкция и эквивалентность ?
Равносильные формулы ИВ
1.Докажите теорему об основных равносильностях (см. приложение 2).
2.Проверьте равносильность формул с помощью таблиц истинности:
а) x Ú z ® y Ù  º
º  Ù
Ù  ; б)a Ù
; б)a Ù  Ú (
Ú ( 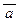 ® b) º
® b) º  ® (
® (  ® a); в) a Ù x ® y º
® a); в) a Ù x ® y º  ;г) a Ù (x ® y) º
;г) a Ù (x ® y) º  ;д) 0 ®
;д) 0 ® 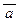 º
º  ;
;
е) a « 1 ® 0Ú 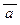 º a Ú 1; ж)
º a Ú 1; ж) 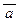 ® 1 Ù
® 1 Ù  « 0 º
« 0 º 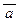 Ù b; з) (a ® 1) Ú (0 Ù 1) º 1.
Ù b; з) (a ® 1) Ú (0 Ù 1) º 1.
3.С помощью основных равносильностей приведите равносильные формулы предыдущего задания к одинаковому виду. Докажите неравносильность остальных формул предыдущего задания, предварительно упростив их с помощью равносильных преобразований.
4.Каким условиям должны удовлетворять формулы А и B для того, чтобы выполнялись следующие свойства ?
а) А Ú B º A Ù B, б) A ® B º B ® A, в) A Ù  º
º  Ù B, г) (В ® A) ® (
Ù B, г) (В ® A) ® (  ®
®  ) º 1, д)
) º 1, д)  º
º  Ù A, е) А Ù (
Ù A, е) А Ù (  Ú
Ú  ) º В Ù
) º В Ù  , ж)
, ж)  º
º  Ù A, з) А Ú B º A Ù B, и) (
Ù A, з) А Ú B º A Ù B, и) (  ®
®  ) « (В ® A) º 1.
) « (В ® A) º 1.
5.Используя основные равносильности, упростите формулы:
а)  ® ((P Ú Q) ® P); б) (x « y) Ù (x Ú y); в) (a ® b) Ù (b ®
® ((P Ú Q) ® P); б) (x « y) Ù (x Ú y); в) (a ® b) Ù (b ® 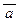 ) Ù (c ® a); г) p ® q ® p ® q; д)
) Ù (c ® a); г) p ® q ® p ® q; д)  Ú y ® x « x ®
Ú y ® x « x ®  Ú y ; е)
Ú y ; е)  Ù x Ú y ®
Ù x Ú y ®  «
«  Ù y Ú x ® x;
Ù y Ú x ® x;
 .
.
6.Приведите формулы предыдущего задания к дизъюнктивной и конъюнктивной формам.
7.Приведите следующие формулы к дизъюнктивной и конъюнктивной формам:
а) ((u ® v) ® (w ®  )) ® (
)) ® (  ®
®  ); б) (
); б) (  Ù
Ù  « x) Ù (x ® y ) ®
« x) Ù (x ® y ) ®  ;
;
в) (p Ú q) Ù  Ú p Ù q Ú (
Ú p Ù q Ú (  Ù p); г) u ® v ®
Ù p); г) u ® v ®  ®
®  ®
®  ® w ;
® w ;
д) (u ® (v ® w)) ® ((u ®  ) ® u); е) x Ù (y Ú
) ® u); е) x Ù (y Ú  ) Ù (
) Ù (  Ú x) Ú (
Ú x) Ú (  Ù y);
Ù y);
ж) (A Ú  ® C) ® (A ® B Ù
® C) ® (A ® B Ù  Ú
Ú  ); з) (p Ù q ®
); з) (p Ù q ®  ) Ù
) Ù  Ú
Ú  Ù q ;
Ù q ;
и) u Ù v Ú  ® (u Ù v) Ú
® (u Ù v) Ú  ®
®  Ù
Ù  ; к) (A Ú
; к) (A Ú  Ù C) Ù (A Ú B Ù
Ù C) Ù (A Ú B Ù  Ú
Ú  ).
).
8.Запишите следующие формулы, используя только знак отрицания и логические связки а) Ù, Ú , б) Ù, ® , в) Ú , ® : 1) ((x Ú  ® z) ® (z Ù x « y)) Ù (
® z) ® (z Ù x « y)) Ù (  Ù
Ù  Ú
Ú  ), 2)x Ù y Ú y Ù z Ú x Ù z, 3)
), 2)x Ù y Ú y Ù z Ú x Ù z, 3)  Ù
Ù  Ù
Ù  Ù
Ù  Ú
Ú  Ù
Ù  , 4) x Ú y Ù y Ú z Ù x Ú z, 5) (
, 4) x Ú y Ù y Ú z Ù x Ú z, 5) (  Ú
Ú  ®
®  Ú
Ú  ) «
) «  Ú
Ú  .
.
9.Можно ли формулу  Ú
Ú  записать, используя только связки Ù , Ú , но не используя отрицания ? А с помощью Ú и ® , но не используя отрицания ? А используя связки Ù , Ú и ® , но не используя отрицания ?
записать, используя только связки Ù , Ú , но не используя отрицания ? А с помощью Ú и ® , но не используя отрицания ? А используя связки Ù , Ú и ® , но не используя отрицания ?
10.Докажите, что заменив любую подформулу в формуле ИВ на равносильную ей, получим формулу, равносильную исходной.
11.Верно ли, что если A º B и С º D то AC = BD ? Приведите пример, показывающий, что равенство AB = CD справедливо не всегда.
СДНФ и СКНФ
1.Постройте СДНФ и СКНФ формул: а) (a ® b) Ù 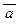 « bÚ a ;б) a ®
« bÚ a ;б) a ® 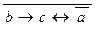 ;в) (x Ú (
;в) (x Ú (  Ù y)) « (x Ú y) ;г)
Ù y)) « (x Ú y) ;г)  ;е) x ®
;е) x ® 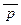 Ú r « s ® x ; ж) (a ® (b ® c)) ® ((a ® b) ® (a ® c)) ; з)
Ú r « s ® x ; ж) (a ® (b ® c)) ® ((a ® b) ® (a ® c)) ; з)  ; и) (p ® q) Ù (q ®
; и) (p ® q) Ù (q ®  ) Ù (r ® p) ;к)a ® a Ú b ; л)(x ® y) ® ((x ® (y ® z)) ® (x ® z)) ; м)x ® y ® x ; н)x ® y Ù (x ® y) ; о) ((a ® b) ® ((a ® c) ® (a ® b Ù c))) ; п) (x ® z) ® ((y ® z) ® (x Ú y ® z)) ; р)
) Ù (r ® p) ;к)a ® a Ú b ; л)(x ® y) ® ((x ® (y ® z)) ® (x ® z)) ; м)x ® y ® x ; н)x ® y Ù (x ® y) ; о) ((a ® b) ® ((a ® c) ® (a ® b Ù c))) ; п) (x ® z) ® ((y ® z) ® (x Ú y ® z)) ; р)  .
.
2.Приведите формулы задания 1 к СДНФ и СКНФ с помощью равносильных преобразований формул.
3.Приводя формулы к СДНФ или СКНФ, проверьте равносильность формул:
а) (x ® y) º  ;б)
;б)  º (x Ù
º (x Ù  ) Ú (
) Ú (  Ù z) ;в) (x ® y Ù
Ù z) ;в) (x ® y Ù  ) º
) º  ;г) x Ú y ®
;г) x Ú y ®  º
º  Ú y ; д)
Ú y ; д)  º (x Ù
º (x Ù  ) Ú (
) Ú (  Ù y) ; е) x ®
Ù y) ; е) x ®  º
º  Ú y ; ж)
Ú y ; ж) 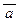 ® 1 Ù
® 1 Ù  « 0 º
« 0 º 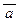 Ù b ; з) a Ù y ® x º
Ù b ; з) a Ù y ® x º  ;и) 0 ®
;и) 0 ® 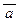 º
º  .
.
4.Классифицируйте формулы, приведя их к СДНФ или СКНФ :а)  ;б) a Ú b Ù (
;б) a Ú b Ù (  Ú c ® b) ® c ® b;в) a ®
Ú c ® b) ® c ® b;в) a ® 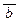 Ù c Ú b «
Ù c Ú b « 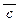 ;г) u Ú (v Ù w) ® w Ù u ; д) a Ú
;г) u Ú (v Ù w) ® w Ù u ; д) a Ú 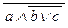 «
« 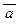 Ù b ®
Ù b ® 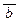 ; е)
; е)  ;ж) v ® (w Ú u) Ù v ;з) a «
;ж) v ® (w Ú u) Ù v ;з) a « 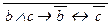 ® b Ú c ; и) p ® u Ú
® b Ú c ; и) p ® u Ú 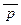 «
«  Ù v ® p Ú
Ù v ® p Ú 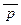 .
.
5.Постройте формулу от трёх переменных, которая истинна тогда и только тогда, когда ровно две из этих переменных ложны.
6.Постройте формулу от трёх переменных, которая принимает такое же значение, как и большинство её переменных.
7.Найдите такую формулу X, что
а) ((X Ù y) ®  ) ® ((z ®
) ® ((z ®  ) ® X) – закон логики;
) ® X) – закон логики;
б) ((r ® (  Ù p)) ® X) ® (X Ù (p ® q)Ù r) – закон логики;
Ù p)) ® X) ® (X Ù (p ® q)Ù r) – закон логики;
в) ((X Ù y) ®  ) ® ((z ®
) ® ((z ®  ) ® X) – противоречие;
) ® X) – противоречие;
г) ((r ® (  Ù p)) ® X) ® (X Ù (p ® q)Ù r) – противоречие;
Ù p)) ® X) ® (X Ù (p ® q)Ù r) – противоречие;
в) X ® (p Ú q Ù  ) º p ® (q Ú r Ù
) º p ® (q Ú r Ù  );
);
г) u Ú X Ù v Ú X º X ® u Ù X ® v.
8.Почему импликация не выражается через конъюнкции и дизъюнкции без использования отрицания ? Можно ли выразить эквивалентность через импликацию и дизъюнкцию ?
9.Докажите, что если дизъюнкция конъюнкцийтождественно ложна, то в каждой конъюнкции некоторая переменная участвует вместе со своим отрицанием.
10.Докажите, что если конъюнкция дизъюнкцийтождественно истинна, то в каждой дизъюнкции некоторая переменная участвует вместе со своим отрицанием.
11.Докажите, что формула, записанная только с помощью связки « , является законом логики тогда и только тогда, когда каждая переменная в ней участвует чётное число раз.
12.Докажите, что формула, записанная только с помощью связок « и  , является законом логики тогда и только тогда, когда каждая переменная в ней и связка
, является законом логики тогда и только тогда, когда каждая переменная в ней и связка  участвует чётное число раз.
участвует чётное число раз.
13.Докажите, что равносильные СКНФ отличаются только порядком своих совершенных элементарных дизъюнкций.
14.Постройте наиболее простые РКС по функциям проводимости:
а) (a ® b) Ú (b ® a);б) x Ú (  Ù y) ® (x Ú y);в) (x Ú y Ú z) Ù (x Ù
Ù y) ® (x Ú y);в) (x Ú y Ú z) Ù (x Ù  « x Ù
« x Ù  );
);
г) (((x Ù  ®
®  ) ®
) ®  ) Ú
) Ú  Ù z) Ù y ; д) (a « b) Ú (
Ù z) Ù y ; д) (a « b) Ú (  ) Ù a ® b ; е)
) Ù a ® b ; е)  ® y ; ж) (p Ú q) Ù
® y ; ж) (p Ú q) Ù  Ú p Ù q Ú (
Ú p Ù q Ú (  Ù p) ; з) (p Ù q ®
Ù p) ; з) (p Ù q ®  ) Ù
) Ù  Ú
Ú  Ù q ; и) a Ù b « a Ú b .
Ù q ; и) a Ù b « a Ú b .
15.
 |
УпроститеРКС:
16.Проверьте равносильность РКС:


17.Постройте РКС
а) с четырьмя переключателями, зажигающую лампочку, если, и только если, включены ровно два из них;
б)с четырьмя переключателями, зажигающую лампочку, если включено два или три из них;
в) с четырьмя переключателями, зажигающую лампочку тогда и только тогда, когда включены переключатели с чётными номерами, но выключены переключатели с нечётными номерами.
18.Пусть S(x, y, T) = (x Ù y Ù  ) Ú (x Ù
) Ú (x Ù 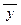 Ù T) Ú (
Ù T) Ú (  Ù
Ù 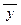 Ù T) Ú (x Ù y ÙT),
Ù T) Ú (x Ù y ÙT),
R(x, y, T) = (x Ù 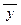 Ù
Ù  )Ú (
)Ú (  Ù y Ù
Ù y Ù  ) Ú (
) Ú (  Ù
Ù 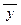 Ù T) Ú (x Ù y ÙT).
Ù T) Ú (x Ù y ÙT).
Докажите, что S(x, y, T) º (x Ù y) Ú (x Ù T) Ú (y Ù T),
R(x, y, T) º (x Ù y Ù T) Ú  Ù (x Ú y Ú T),
Ù (x Ú y Ú T),
и постройте интегральную схему с тремя входами x , y , T и двумя выходами R , S .
Булевы функции
1.Задайте табличным способом следующие булевы функции:
а) f(x) = x2; б) g(x) = (x3 + 4×x – 3) mod 2; в) h(x) = min{f(x), g(x)}; г) k(x, y) = x×g(x)y;
д) а(x, y) = (x Ù y ® x) + x2 – y2 (mod 2); е) max{a(x, y), k(x, y)}; ж) xh(x)×ya(x, y).
2.Задайте табличным способом следующие булевы функции: 
 .
.
3.Задайте формулами следующие булевы функции: а) формулами ИВ, б) полиномами Жегалкина, в) другими формулами на Ваш вкус.
| x | y | f0 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| x | y | z | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
4.Следующие формулы запишите в виде полиномов Жегалкина:
а) ; б) x Ù y ®
; б) x Ù y ®  ;в)
;в)  ; г)xÙ
; г)xÙ 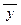 Ú
Ú  Ù y; д)a ®
Ù y; д)a ® 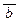 Ù c Ú b «
Ù c Ú b « 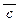 ; е)
; е)  ; ж) p Ù (q ® r) ® (p Ù q); з) x ®
; ж) p Ù (q ® r) ® (p Ù q); з) x ®  ;и)
;и)  ; к) x ® y Ú z; л)
; к) x ® y Ú z; л) ; м)
; м)  ; н) a ® (b ® b) ® a; о)
; н) a ® (b ® b) ® a; о)  Ù x Ú y ®
Ù x Ú y ®  «
«  Ù y Ú x ® x .
Ù y Ú x ® x .
5.Для следующих полиномов Жегалкина найдите СДНФ и СКНФ:
а) a + b + 1; б) u×v + u; в) a×b + b + a + 1; г) x×y×z + x×z +y; д) x×z + y×z + x×y; е) x×y×z×p + x×z + 1; ж) x×y×z×p + x×y + y×p + x×z + 1; з) x×(y + z) + y×(x + z) + 1.
6.Запишите в виде полиномов Жегалкина булевы функции заданий 1, 2.
7.Запишите в виде полиномов Жегалкина: а) отрицание произвольного полинома Жегалкина; б) дизъюнкцию двух произвольных полиномов Жегалкина; в) x1 Ú … Ú xn ; г)  ; д)
; д)  .
.
8.Сколько полиномов Жегалкина от n переменных
а) обращаются в ноль при нулевых значениях аргументов ?
б) обращаются в единицу при нулевых значениях аргументов ?
в) полилинейны (т.е. линейны по каждому аргументу) ?
г)являются мономами ? А суммой двух мономов ?
д)принимаютзначение 1 при единичных значениях аргументов ?
9.Найдите все полилинейные булевы функции от двух аргументов.
10.Найдите все булевы функции от двух аргументов, обращающиеся в ноль при нулевых значениях аргументов, а также все функции, принимающиезначение 1 при единичных значениях аргументов.
11.Пусть задан полином Жегалкина p(x1 , … , xn). Как найти все аннулирующие полиномы Жегалкина q(x1 , … , xn), для которых p(x1 , … , xn)×q(x1 , … , xn) = 0 ? Найдите все аннулирующие полиномы для
а) p(x) = x, б) p(x) = 1+x,б) p(x, y) = x+y, в) p(x, y) = x+x×y, г) p(x, y) = 1+x+y+x×y, д) p(x, y, z) = x + y + x×z, е) p(x, y, z) = x + z + x×z, ж) p(x, y, z) = 1+ x + y×z.
12.Докажите, что любая натуральная степень полинома Жегалкина равна исходному полиному.
Логическое следование.
