Алгоритм нахождения раскраски.

1. Выделить все пустые подграфы графа.

2. Построить таблицу покрытий вершин графа пустыми подграфами.

3. Найти минимальное покрытие вершин графа пустыми подграфами (мощность минимального покрытия – это h(G), а само покрытие определяет раскраску).

Оценки значения хроматического числа:

· Граф бихроматичен ( 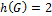), если в нем отсутствуют циклы нечетной длины.

· Любой планарный граф может быть раскрашен не более, чем в 4 цвета.

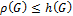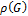· , где –плотность графа – число максимального полного подграфа.

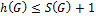· , где 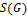– степень графа – максимальная степень его вершин.

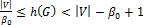· , где 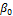–число внешней устойчивости – минимальная мощность множества 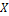таких вершин, что каждая вершина графа или принадлежит кXили смежна с одной из вершин из .

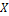Оценки хроматических чисел результатов операций:

· ;

· ;

· ;

·

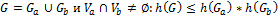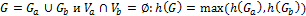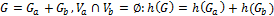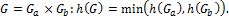
Приближенная раскраска по Ершову:

Алгоритм строится на стягивании несмежных вершин в одну, при этом в результате стягивания ребра стянутых вершин объединяются. Процесс стягивания производится до тех пор пока не будет достигнут полный граф. Вершины результирующего графа, состоящие из нескольких вершин исходного графа, раскрашиваются в один цвет.

Алгоритм Ершова дает лишь оценочную раскраску графа, а полученное число красок является оценкой хроматического числа сверху.

Пример.

15. Машина Тьюринга, ее структура и свойства. Проблема остановки МТ.

Алгоритм– точное предписание о выполнении в некотором порядке системы операций, определяющихпроцесс перехода от исходных данных к искомому результату для решения всех задач некоторого типа.

Свойства:

1. Определенность–точность, не оставляющая место произволу;

2. Массовость – применимость для любых допустимых исходных данных;

3. Результативность– гарантия результата для любых допустимых данных;

4. Элементарностьшагов.

Формальное описание алгоритмов былонеобходимо, т.к.:

1. было необходимо обоснование существания проблем, для которых не существует алгоритма;

2. было необходимо выявить конечность алгоритма, элементарные шаги;

3. были попытки создать универсальный алгоритм;

4. возникла необходимость рассматривать алгоритм как математический объект.

Машина Тьюринга - абстрактная (воображаемая) "вычислительная машина" некоторого точно охарактеризованного типа, дающая пригодное для целей математического рассмотрения уточнение общего интуитивного представления об алгоритме.

Тезис Тьюринга - любой алгоритм можно преобразовать в машину Тьюринга.

Структура машины Тьюринга.

1. Бесконечная лента, разделенная на ячейки, в которых записаны символы внешнего алфавита 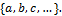Выделяют два специальных символа - пустой символ и символ начала строки.

2. Механическое устройство, способное перемещаться относительно ленты (вправо, влево, стоять на месте).

3. Управляющая головка - некоторое устройство, способное считывать значение ячейки и записывать новое.

4. Выделенная ячейка памяти, содержащая сведения о внутреннем состоянии машины – символа из внутреннего алфавита 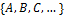. Выделяют для специальных символа - начальное и заключительное состояния.

5. Функциональная схема – область памяти с программой, содержащие инструкции вида: 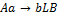–если машина находится в состоянии 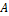, а на ленте находится символ 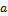, то записать на ленту 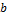, сделать шаг влево и перейти в состояние .

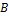Проблема называется алгоритмически неразрешимой, если для нее невозможно построить алгоритм.

Теорема. Задача об остановке машины Тьюринга на произвольном входном слове алгоритмически неразрешима.

Будем вести доказательство от противного.

Пусть 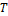– машина Тьюринга, 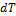– ее код, t- начальное слово.

Предположим, что существует машина 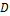, решающая проблемы остановки машины 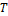. На ленте машины 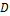перед запуском записано кодмашины 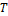и начальное слово t.Машина 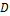работает и печатает «+» если машины 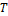останавливается, и «-» в противном случае.

Если предположение верно в общем смысле, то и в частном тоже. Пусть 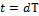.Машину 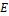получим следующим образом: сначала 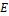копирует на ленту 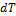в прямом порядке, а потом работает как машина .

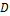Теперь преобразуем машину 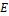в машину 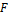, которая работает так же как и машина 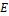вплоть до остановки машины 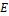, но если при слове 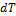машина 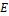печатает «+» и останавливается, то машина 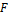не останавливается, а двигается по ленте неограниченно вправо. А если машина 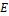печатает «-», то Fостанавливается.Итак, машина 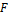не останавливается, если 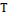останавливается и машина 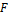останавливается, если машина 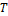не останавливается.

Пусть теперь 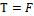. Тогда F – самоанализируюая машина, в качестве входного слова ее же код. Тогда машина 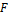остановится, если машина 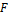не остановится, и машина 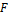не остановится, если машина 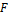остановится. Противоречие 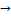задача алгоритмически неразрешима.