КОНТРОЛЬНАЯ РАБОТА №1 Тема: Алгебра логики
1. Построить таблицу функции алгебры логики от 4 переменных, принимающую значение 1 только на тех наборах (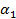 
, 
, 
, 
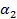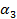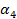), которые удовлетворяют следующему условию: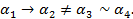 
2. Функции f и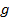 
заданы векторно. Построить векторное представление функции h:
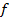= (0010), 
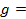(1101),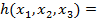 
( 
, 
) 
( 
, ( , )).
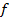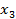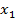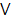
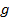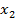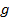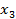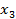3. Построить таблицу функции, заданной формулой: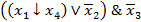 
.
4. Проверить эквивалентность формул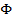 
и 
:
, 
( 
) 
( 
).
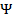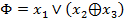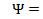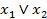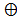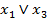5. Используя основные эквивалентности, доказать (или опровергнуть) эквивалентность формул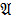 
и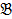 
: 
, 
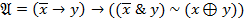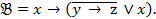
6. Представить функцию 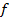в виде СДНФ и СКНФ: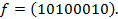 
7. Используя основные эквивалентности, построить полином Жегалкина для следующей функции, заданной формулой: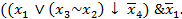 
8. Представить функцию 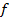в виде полинома Жегалкина, построив предварительно СДНФ:
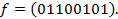
9. Представить функцию 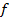в виде полинома Жегалкина, используя метод неопределенных коэффициентов: 
( 
.
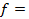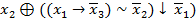10. Определить существенные и фиктивные переменные функции :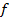
( 
.
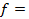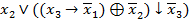11. Определить существенные и фиктивные переменные функции, пребразовав ее предварительно в полином Жегалкина: (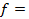 
.
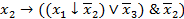12. Пользуясь принципом двойственности, построить функцию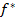 
, двойственную к заданной функции : 
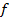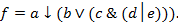
13. Установить, является ли функция 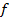линейной: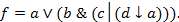 
14. Установить, является ли функция 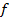монотонной: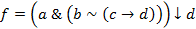 
15. Проверить принадлежность функции 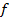к классам 
, 
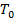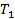, S, M, L: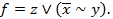 
16. Проверить полноту (или доказать неполноту) системы функций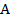 
: 
.
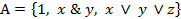17. Проверить полноту системы функций 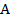. Если система полна, то выделить все её базисы. 
.
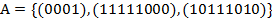18. Если система функций 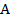полна, то выделить все её базисы:
.
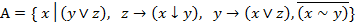19. Найти длину СДНФ заданной функции (где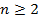 
): 
.
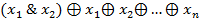20. Доказать: если f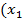 
, ,…, 
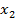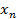) – тождественно истинная функция, то функция, получающаяся из f заменой переменных на их отрицания, – также тождественно истинная функция.
21. Доказать, что функцию f нельзя реализовать формулой над S: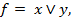 
S 
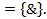
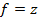
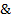
22. Реализовать функцию f формулой над 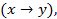S: 
S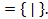 
23 а. При каких n функция f является самодвойственной:
) 
).
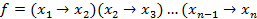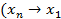23 б. При каких n функция f является монотонной: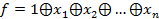 
.
24. При каких n функция f является шефферовой, т.е. образует полную систему:
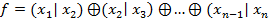
ВАРИАНТ № 9
КОНТРОЛЬНАЯ РАБОТА № 1
Тема: Алгебра логики
1. Построить таблицу функции алгебры логики от 4 переменных, принимающую значение 1 только на тех наборах ( 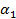, , 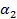, 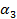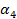), которые удовлетворяют следующему условию:
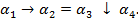
2. Функции f и 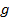заданы векторно. Построить векторное представление функции h:
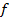= (0100), 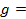(1101), (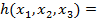 
( , )) ( , ).
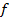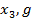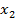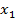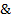
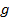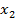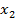3. Построить таблицу функции, заданной формулой: (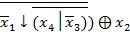 
4. Проверить эквивалентность формул 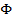и :
, 
( ) 
( ).
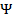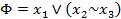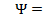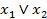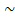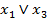5. Используя основные эквивалентности, доказать (или опровергнуть) эквивалентность формул 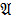и : 
( 
( 
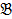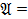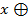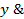z))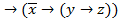 
, 
.
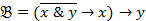6. Представить функцию 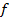в виде СДНФ и СКНФ: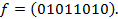 
7. Используя основные эквивалентности, построить полином Жегалкина для следующей функции, заданной формулой: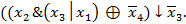 
8. Представить функцию 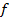в виде полинома Жегалкина, построив предварительно СДНФ:
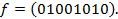
9. Представить функцию 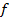в виде полинома Жегалкина, используя метод неопределенных коэффициентов: ( 
.
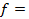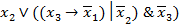10. Определить существенные и фиктивные переменные функции :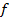
( 
.
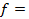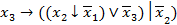11. Определить существенные и фиктивные переменные функции, пребразовав ее предварительно в полином Жегалкина: (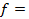 
.
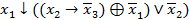12. Пользуясь принципом двойственности, построить функцию 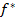, двойственную к заданной функции :
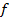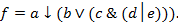
13. Установить, является ли функция 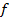линейной: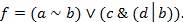 
14. Установить, является ли функция 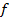монотонной:
1) 
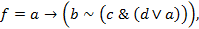
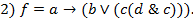
15. Проверить принадлежность функции 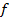к классам 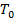, , 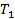S, M, L: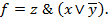 
16. Проверить полноту (или доказать неполноту) системы функций :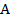
.
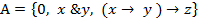17. Проверить полноту системы функций 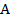. Если система полна, то выделить все её базисы. 
.
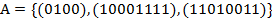18. Если система функций 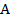полна, то выделить все её базисы:
.
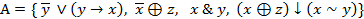19. Найти длину СДНФ (т.е. число наборов, на которых функция равна 1) заданной функции (где ):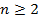 
.
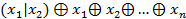20. Доказать: если f 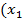, ,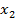…, 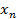) – тождественно истинная функция, то функция, получающаяся из f заменой переменных на их отрицания, – также тождественно истинная функция.
21. Доказать, что функцию f нельзя реализовать формулой над S: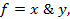 
S 
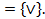
22. Реализовать функцию f формулой над 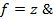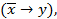S: 
S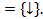 
23 а. При каких n функция f является самодвойственной:
) 
) 
.
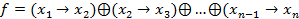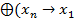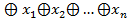23 б. При каких n функция f является монотонной: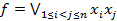 
.
24. При каких n функция f является шефферовой, т.е. образует полную систему:
).
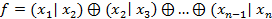ВАРИАНТ 10