Если отрицается основание условной посылки, то вывод может быть только вероятным.

Примеры:

Если число делится на четыре, то оно делится на два. Число не делится на четыре. Вероятно, оно не делится на два.

а  b а вероятно, b

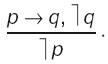Схема отрицающего модуса:

Условно-категорическое умозаключение состоит из двух посылок — условного и категорического суждений. При этом категорическая посылка обычно состоит из тех же терминов, что и основание или следствие условной посылки. Например: "Если государственная система образования получит поддержку, то вузы Украины преодолеют трудности.

Государственная система образования получит поддержку. Следовательно, вузы Украины преодолеют трудности".

Условно-категорическое умозаключение имеет два модуса — утверждающий и отрицающий.

В утверждающем модусе заключение идет от утверждения основания к утверждению следствия. Общая схема этого модуса такова: если есть А, то есть В; есть А, следовательно, есть и В.

Вывод по этому модусу может быть и утвердительным, и отрицательным. Качественная сторона вывода находится в прямой зависимости от качественного характера условной посылки.

В отрицающем модусе заключение идет от отрицания следствия к отрицанию основания. Схематически отрицающий модус можно записать так: если есть А, то есть и В; нет В, следовательно, нет и А.

Вывод по этому модусу также бывает утвердительным и отрицательным; его качественная сторона находится в обратной зависимости от качественного характера условной посылки.

Нередко в условной посылке основание и следствие различны по качественному характеру. В таком случае категорическая посылка по качеству должна быть обратной качественному характеру следствия, а вывод будет обратным (в качественном отношении) основанию условной посылки. В общей схеме это выглядит так: если есть А, то нет В; есть В, следовательно, нет А.

Учитывая, что явление может обусловливаться различными причинами, в условно-категорическом умозаключении нельзя идти от отрицания основания к отрицанию следствия или от утверждения следствия к утверждению основания (ибо это следствие может иметь иное основание).

Умозаключение — это третья (после понятия и суждения) форма мышления, в которой из одного, или двух, или нескольких суждений, называемых посылками, вытекает новое суждение, называемое заключением, или выводом. В логике принято располагать посылки и вывод друг под другом и отделять посылки от вывода чертой:

В приведенном примере первые два суждения являются посылками, а третье — выводом. Понятно, что посылки должны быть истинными суждениями и должны быть связаны между собой. Если хотя бы одна из посылок ложна, то и вывод ложен:

Как видим, в приведенном примере ложность первой посылки приводит к ложному выводу, несмотря на то, что вторая посылка является истинной. Если посылки между собой не связаны, то вывод из них сделать невозможно. Дедуктивные умозаключения или дедукция (от лат. deductio — выведение) — это умозаключения, в которых из общего правила делается вывод для частного случая (из общего правила выводится частный случай).

Например:

Как видим, первая посылка представляет собой общее правило, из которого (при помощи второй посылки) вытекает частный случай в виде вывода: если все звезды излучают энергию, значит Солнце тоже ее излучает, потому что оно является звездой. В дедукции рассуждение идет от общего к частному, от большего к меньшему, знание сужается, в силу чего дедуктивные выводы достоверны, т.е. точны, обязательны, необходимы и т.п. Индуктивные умозаключения или индукция (от лат. inductio — наведение) — это умозаключения, в которых из нескольких частных случаев выводится общее правило (несколько частных случаев как бы наводят на общее правило). Например:

Как видим, первые три посылки представляют собой частные случаи, четвертая посылка подводит их под один класс объектов, объединяет их, а в выводе говорится обо всех объектах этого класса, т.е. формулируется некое общее правило (вытекающее из трех частных случаев). Легко увидеть, что индуктивные умозаключения строятся по принципу, противоположному принципу построения дедуктивных умозаключений. В индукции рассуждение идет от частного к общему, от меньшего к большему, знание расширяется, в силу чего индуктивные выводы, в отличие от дедуктивных, не достоверны, а вероятностны. Умозаключения по аналогии или просто аналогия (от греч. analogia — соответствие) — это умозаключения, в которых на основе сходства предметов (объектов) в одних признаках делается вывод об их сходстве и в других признаках. Например:

Как видим, сравниваются (сопоставляются) два объекта (планета Земля и планета Марс), которые сходны между собой в некоторых существенных, важных признаках (находиться в солнечной системе, иметь атмосферу и воду). На основе данного сходства делается вывод о том, что, возможно, эти объекты сходны между собой и в других признаках: если на Земле есть жизнь, а Марс во многом похож на Землю, то не исключено наличие жизни и на Марсе. Выводы аналогии, как и выводы индукции, вероятностны.

Полная индукция — это умозаключение, в котором на основе принадлежности каждому элементу или каждой части класса оп­ределенного признака делают вывод о его принадлежности классу в

целом.

Индуктивные умозаключения такого типа применяются лишь в тех случаях, когда имеют дело с закрытыми классами, число элемен­тов в которых является конечным и легко обозримым. Например, число государств в Европе, количество промышленных предпри­ятий в данном регионе, число субъектов федерации в данном госу­дарстве и т.п.

Схема умозаключения полной индукции имеет следующийвид:

Посылки:

1) S1 имеет признак Р

S2 имеет признак Р

Sn имеет признак Р

2) S1, S2,..., Sn — составляют класс К

Заключение:

Всем предметам класса К присущпризнак Р

Выраженная в посылках этого умозаключения информация о каждом элементе или каждой части класса служит показателемпол­ноты исследования идостаточным основанием для логического переноса признака на весь класс. Тем самым вывод в умозаключении полной индукции носитдемонстративныйхарактер. Это означает, что при истинности посылок заключение в выводе будетнеобходимо истинным.

Познавательная роль умозаключения полной индукции проявля­ется в формировании нового знания оклассе илироде явлений. Логический перенос признака с отдельных предметов на класс в целом не является простым суммированием. Знание о классеилироде — этообобщение, представляющее собой новую ступень в развитии знания.

Индукция через простое перечисление при отсутствии противоречащего случая, по другому называемая еще популярной индукцией, есть общий вывод на основании лишь того, что из всех первых, даже случайно попавшихся случаев (фактов), не встретилось ни одного, противоречащего обобщению. Примером этого вида индукции является случай с незадачливым путешественником, который, едва высадившись на берег Франции, встретил нескольких, случайно оказавшихся рыжими, французов и записал в своем дневнике: "Все французы — рыжие". Или другой пример: аспирант пришел помочь своему научному руководителю принять экзамен у студентов, и, явно желая польстить ему, после первых же успешных ответов экзаменующихся, сказал профессору: "Ваши студенты очень хорошо подготовились к экзамену".

Степень достоверности (вероятности) вывода по индукции через простое перечисление существенно зависит от количества рассматриваемых случаев: чем больше их число, тем выше достоверность вывода.

Причинная связь между явлениями определяется посредст­вом ряда методов, (описание и классификация которых восхо­дит еще к ф. Бэкону и которые были развиты Дж. Ст. Миллем.

Метод сходства

Требуется выяснить причину какого-то явления а. Исходя из определения причины как явления или совокупности явлений, кото­рые предшествуют другому явлению и вызывают его, в данном случае - явление а, будем анализировать предшествующие а яв­ления. В первом случае появления аему предшествовали обсто­ятельства АВС во втором случае - ADE, в третьем случае пе­ред появлением а имели место обстоятельства АКМ. Что мог­ло быть причиной а? Так как во всех трех случаях общим обстоятельством было А, а все остальные обстоятельства были различны, то можно сделать вывод, что, вероятно, А является причиной или частью причины явления а.

Случаи появления события а	Предшествующие обстоятельства	Наблюдаемое явление
	АВС	а
	ADE	а
	АКМ	а

Вероятно, А есть причина а.

Примером применения метода единственного сходства яв­ляется выяснение причинызаболевания трех человек энцефа­литом. В первом случае заболеванию энцефалитом одного человека предшествовали события: А -укус иксодового клеща;

В - начало летнего периода; С- пребывание в тайге на Урале. Во втором случае заболеванию предшествовали такие собы­тия: А - укус иксодового клеща; D - весенний период; Е -пребывание в лесистом районе Восточной Сибири. В третьем случае заболеванию предшествовали обстоятельства: А - укус иксодового клеща; К - конец летнего периода; М - пребыва­ние в березовом лесу Алтая. Общим во всех трех случаях заболевания энцефалитом был укус иксодового клеща, что и явилось возможной причиной заболевания.

Если наблюдаемые случаи какого-либо явления имеют об­щим лишь одно обстоятельство, то оно и есть, очевидно, причина данного явления. Метод этот связан с наблюдением.

Метод различия

Рассматриваются два случая, различающиеся тем, что в пер­вом случае явление а наступает, а во втором - нет. При исследо­вании предшествующих обстоятельств установлено, что все они как в первом, так и во втором случаях были сходными, кроме, однако, одного, которое в первом случае присутствовало, а во вто­ром - отсутствовало, т. е. были обстоятельства ABCD (в пер­вом случае) и обстоятельства BCD (во втором).

Случаи	Предшествующие обстоятельства	Наблюдаемое явление
	ABCD	а
	BCD	—

Вероятно, А есть причина а.

Метод различия связан не с наблюдением, а с эксперимен­том, ибо нам приходится произвольно отделять то или другое обстоятельство от других обстоятельств.

Например, в аэропорту, чтобы выяснить, нет ли у пассажиров крупных металлических предметов, им предлагают пройти че­рез устройство, снабженное электромагнитом и присоединенным к нему электрическим звонком. Когда один из туристов группы проходил через данное устройство, зазвенел звонок. Ему предло­жили вынуть из карманов все металлические предметы. После удаления им связки ключей и металлических денег, когда он по­вторно прошел через данное устройство, звонок не зазвенел. Следовательно, умозаключили работники аэропорта, причиной звонка было наличие именно данных металлических предметов у дан­ного пассажира. Все остальные предшествующие обстоятель­ства были теми же самыми.

Если случаи, при которых явление, соответственно, насту­пает или не наступает, различаются только одним предшест­вующим обстоятельством, а все другие обстоятельства тождественны, то именно это обстоятельство и есть при­чина данного явления.

Другой пример. Если человек съел клубнику и после этого у него, появилась аллергическая реакция, а все другие пищевые продукты оставались прежними и в последующие дни, когда он не ел клубнику и у него не было аллергических реакций, то врач правильно сделал вывод, что именно клубника вызвала у данно­го больного аллергию.

Метод сопутствующих изменений

Если при изменении предшествующего обстоятельства А изменяется и изучаемое нами явление а. а все остальные предшествующие обстоятельства, например В, С, D, Е, оста­ются неизменными, тоА является причиной а.

Например, если мы увеличим скорость движения в два раза, то за то же самое время пройденный путь тоже увеличится в два раза. Следовательно, увеличение скорости есть причина увеличения пройденного пути за тот же промежуток времени. S = v • t - формула равномерного движения, устанавливающая, что при изменении v или t (скорости движения или времени движе­ния) прямо пропорционально изменяется и путь (величина S).

Трение есть причина нагревания тела; увеличение длины ме­таллического стержня при его нагревании и другие примеры ил­люстрируют применение метода сопутствующих изменений. При этом мы не можем отделить трение от нагревания тела, поэто­му не могли бы использовать метод различия для установления причины нагревания тела.

Если изменение одного обстоятельства всегда вызывает изменение другого, то первое обстоятельство есть причина второго.

Метод остатков

Пусть изучаемое явление Kраспадается на несколько однород­ных частей: a, b, с, d. Установлено, что ему предшествуют об­стоятельства А, В, С. При этом известно, что А является причи­ной а. В -причиной b, С- причиной с. Должно быть сходное с. А, В, С обстоятельство D, которое является причиной остающего­ся необъясненным явления d.

Примером, иллюстрирующим этот метод, является открытие планеты Нептун. Наблюдая за величинами отклонения планеты Уран от вычисленной для нее орбиты, учли отклонения на вели­чины а, b, с, которые вызваны наличием влияния планет А, В, С. Но Уран отклонялся еще на величину d. Сделали заключение, что должна существовать неизвестная планета D которая и вызыва­ет это отклонение. У. Леверье рассчитал положение этой неизве­стной планеты, а в 1846 г. И. Галле, построив телескоп, нашел ее на небесной сфере. Так была открыта планета Нептун.

Если известно, что причиной исследуемого явления не слу­жат необходимые для него обстоятельства, кроме одного, то это одно обстоятельство и есть, вероятно, причина дан­ного явления.

Все рассмотренные методы установления причинных связей были разработаны английским философом Ф. Бэконом. Они при­меняются чаще всего не изолированно друг от друга, а в соче­тании, дополняя друг друга.

Аналогия

Способы логического перехода от известного к новому знанию не ограничиваются индукцией и дедукцией. Наряду с ними возможен и третий способ: логический переход от известного знания об отдельном предмете или их группе к новому знанию о другом отдельном предмете или другой их группе. Это заключение по аналогии. Аналогия – это такое умозаключение, где от сходства двух предметов в одних признаках делается вывод о сходстве этих предметов и в других признаках. Аналогия отличается как от индукции, так и от дедукции. Главное отличие в том, что мысль перетекает в ней от единичного к единичному, от частного к частному, от общего к общему. Вместе с тем она и связана с ними. С одной стороны, она опирается на знания, добытые дедукцией и индукцией, а с другой - сама доставляет им материал для новых умозаключений.

По характеру уподобляемых объектов различают два вида аналогии: аналогию предметов и аналогию отношений.

Аналогия предметов – умозаключение, в котором объектом уподобления выступают два единичных предмета, события или явления, а переносимым признаком – свойства этих предметов.

Аналогия отношений – умозаключение, в котором объектом уподобления выступают отношения между двумя парами предметов, а переносимым признаком – свойства этих отношений.

Знания, полученные в результате выводов по аналогии, бывают неодинаковыми по своей обоснованности: в одних случаях заключения имеют проблематичный характер, в других – достоверный. Ценность заключений в выводах по аналогии определяется характером исходного знания о сравниваемых объектах: сходстве уподобляемых объектов, различиях между ними, характере зависимости между признаками сходства и переносимым признаком.

Умозаключение по аналогии представляет собой движение мысли от общности одних свойств и отношений у сравниваемых предметов (или процессов) к общности других свойств и отношений. Сущность умозаключения по аналогии может быть представлена следующим образом. Изучаются два предмета (явления), при этом одно уже достаточно исследовано. Во втором предмете (явлении) известны лишь некоторые его признаки. Оба предмета (явления) сравниваются между собой. Если ряд признаков сравниваемых двух предметов (явлений) совпадает, то делается вывод о том, что и остальные признаки второго предмета (явления) будут такими же.

Общая схема умозаключения по аналогии может быть представлена в таком виде:

А обладает признаками а, b, с, d

В обладает признаками а, b, с

Следовательно, В обладает, по-видимому, признаком d

Строгая аналогия

Характерным отличительным признаком строгой аналогии является наличие необходимой связи между сходными признаками и переносимым признаком. Схема строгой аналогии такая:

Предмет A обладает признаками a, b, с, d, e.

Предмет В обладает признаками a, b, с, d.

Из совокупности признаков а, b, с,d необходимо следует e.

Предмет B обязательно обладает признаком e.

Строгая аналогия применяется в научных исследованиях, в математических доказательствах. Например, формулировка признаков подобия треугольников основана на строгой аналогии: "Если три угла одного треугольника равны трем углам другого треугольника, то эти треугольники подобны" (подобие - вид аналогии).

На строгой аналогии основан метод моделирования. Известно, что единство природы обнаруживается в "поразительной аналогичности" дифференциальных уравнений, относящихся к разным областям явлений. В физике эти аналогичные явления весьма часты. Например, аналогичными уравнениями описываются корпускулярно-волновые свойства света и аналогичные свойства электронов. Закон Кулона, определяющий силу электростатического взаимодействия двух неподвижных друг относительно друга точечных зарядов q₁ и q_2,,расстояние между которыми r, выражается формулой:

Аналогичной формулой выражен закон всемирного тяготения Ньютона:

Здесь мы видим строгую аналогию, в которой переносимыми признаками являются не свойства, а отношения между разными объектами (электрическими зарядами и массами вещества), выраженные аналогичной структурой формул.

Строгая аналогия дает достоверный вывод, т. e. истину, обозначаемую в многозначных логиках, в классической логике, в теории вероятностей через 1. Вероятность вывода по строгой аналогии равна 1.

Доказательство – это совокупность логических приемов обоснования истинности какого-либо суждения с помощью других истинных и связанных с ним суждений.

93.

Структура доказательства включает три элемента: тезис, аргументы, демонстрация.

Еt можно показать на схеме, где тезис обозначен символом Т, аргументы –а₁, а₂… а_n, демонстрация знаком импликации(→).

Тезис – это суждение, истинность которого надо доказать

Тезис занимает центральное место в доказательстве. Он отвечает на вопрос: что требуется доказать?

Суждения в качестве тезиса могут быть из самых разных областей связанных с процессом мышления: новые положения науки, теорема, предполагаемая причина возникновения конкретного явления и т.д. Медикам на основание специального исследования необходимо определить болезнь, поставить диагноз; историки стремятся обосновать суждения об историческх фактах.

Аргументы – это те истинные суждения, с помощью которых обосновывается тезис.

Различают несколько видов аргументов:

1. Удостоверенные единичные факты. К такого рода аргументам относится

так называемый фактический материал, т. е. статистические данные о

населении, территории государства, выполнении плана, количестве вооружения,

свидетельские показания, подписи на документах, научные данные, научные

факты. Роль фактов в обосновании выдвинутых положений, в том числе научных,

велика.

2. Определения как аргументы доказательства. Определения понятий

обычно даются в каждой науке. Правила определения и виды определений

понятий были рассмотрены в теме «Понятие», и там же были приведены

многочисленные примеры определений понятий различных наук: математики,

химии, биологии, географии и пр.

3. Аксиомы. В математике, механике, теоретической физике,

математической логике и других науках, кроме определений, вводят аксиомы.

Аксиомы — это суждения, которые принимаются в качестве аргументов без

доказательства.

4. Ранее доказанные законы науки и теоремы как аргументы

доказательства. В качестве аргументов доказательства могут

выступать ранее доказанные законы физики, химии, биологии и других

наук, теоремы математики (как классической, так и конструктивной).

Юридические законы являются аргументами в ходе судебного доказательства.

В ходе доказательства какого-либо тезиса может использоваться не один,

а несколько из перечисленных видов аргументов.

Формой доказательства, или демонстрацией, называется способ логической

связи между тезисом и аргументами.

Приведем пример доказательства. Поль С. Брэгг высказал такой тезис:

«Купить здоровье нельзя, его можно только заработать своими собственными

постоянными усилиями». Этот тезис он обосновывает так: «Только упорная и

настойчивая работа над собой позволит каждому сделать себя энергичным

долгожителем, наслаждающимся бесконечным здоровьем. Я сам заработал

здоровье своей жизнью. Я здоров 365 дней в году, у меня не бывает никаких

болей, усталости, дряхлости тела. И вы можете добиться таких же

результатов!»'

. Он умер в декабре 1976 г. в возрасте 95 лет. Во время катания на доске у побережья Флориды его накрыла гигантская волна. Его оплакивали 5 детей, 12 внуков, 14 правнуков и

тысячи последователей.