Основной показатель качества регрессионной модели

Одни и те же данные можно обрабатывать различными способами.

На первый взгляд, показателем отклонений данных от модели может служить остаточная сумма квадратов SS. Чем этот показатель меньше, тем приближение лучше, значит, и модель лучше описывает реальные данные. Однако это рассуждение годится только для моделей с одинаковым числом параметров. Ведь если добавляется новый параметр, по которому можно минимизировать, то и минимум, как правило, оказывается меньше.

В качестве основного показателя качества регрессионной модели используют оценку остаточной дисперсии

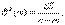
скорректированную на число m параметров, оцениваемых по наблюдаемым данным. В случае задачи восстановления линейной функции одной переменной, рассмотренной в предыдущем подразделе, оценка остаточной дисперсии имеет вид

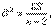
поскольку число оцениваемых параметров m=2.

Почему эта формула отличается от приведенной в предыдущем подразделе? Там в знаменателе n, а здесь - (n-2). Дело в том, что там была рассмотрена непараметрическая теория при большом объеме данных (при 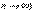. А при безграничном возрастании n разница между n и (n-2) сходит на нет.

Однако при подборе вида модели знаменатель дроби, оценивающей остаточную дисперсию, приходится корректировать на число параметров. Если этого не делать, то придется заключить, что всегда многочлен второй степени лучше соответствует данным, чем линейная функция, многочлен третьей степени лучше приближает исходные данные, чем многочлен второй степени, и т.д. В конце концов доходим до многочлена степени (n-1) с n коэффициентами, который проходит через все заданные точки. Но его прогностические возможности, скорее всего, существенно меньше, чем у линейной функции. Излишнее усложнение статистических моделей вредно.

Типовое поведение скорректированной оценки остаточной дисперсии

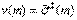
в зависимости от параметра m в случае расширяющейся системы моделей выглядит так. Сначала наблюдаем заметное убывание. Затем оценка остаточной дисперсии колеблется около некоторой константы (теоретического значения дисперсии погрешности).

Поясним ситуацию на примере модели восстановления зависимости, выраженной многочленом:

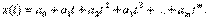
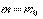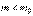Пусть эта модель справедлива при При в скорректированной оценке остаточной дисперсии учитываются не только погрешности измерений, но и соответствующие (старшие) члены многочлена (предполагаем, что коэффициенты при них отличны от 0). При 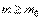имеем

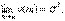
Следовательно, скорректированная оценка остаточной дисперсии будет колебаться около указанного предела. Поэтому в качестве оценки неизвестной статистику степени многочлена (полинома) можно использовать первый локальный минимум скорректированной оценки остаточной дисперсии, т.е.

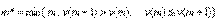
В работе [6] найдено предельное распределение этой оценки степени многочлена.

Теорема.При справедливости некоторых условий регулярности

где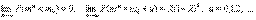

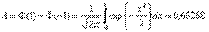
Таким образом, предельное распределение оценки m* степени многочлена (полинома) является геометрическим. Это означает, в частности, что оценка не является состоятельной. При этом вероятность получить меньшее значение, чем истинное, исчезающе мала. Далее имеем:

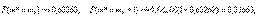
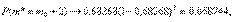
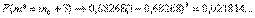
Разработаны и иные методы оценивания неизвестной степени многочлена, например, путем многократного применения процедуры проверки адекватности регрессионной зависимости с помощью статистики Фишера (см. работу [7]). Предельное поведение оценок - таково же, как в приведенной выше теореме, только значение параметра 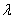иное.

.

Коэф-т детерминации: 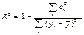. Показывает, какая доля случайных колебаний показателя у учтено в модели и обусловлена случайными колебаниями фактора. 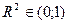и модель тем лучше, чем 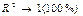. Коэф-т детерминации явл-ся универсальным, т.к. позволяет оценить точность модели, качество в целом, удачность выбора фактора и подходит для случая линейной и нелинейной зависимости переменных.