Резервирование с целой кратностью с постоянно включенным резервом или нагруженное резервирование замещением с абсолютно надежными переключателями

При абсолютно надежных переключателях и индикаторах состояния основной и резервных ветвей в системах с замещающим нагруженным резервом расчет надежности указанных резервированных систем и систем с постоянным резервированием будет одинаковым.

Общее резервирование

Логические схемы резервированных устройств для общего резервирования представлены на рис 4.2, а, 4.2, в. Основная схема (цепь), обозначенная цифрой "1", включает m последовательно по надежности соединенных элементов с интенсивностями отказов λ_0i. Параллельно по надежности с ней включено k резервных цепей, имеющих точно такие же параметры элементов, как и в основной цепи.

Анализ выполним при следующих допущениях:

1) отказы элементов являются случайными и независимыми событиями;

2) основная и резервные цепи равнонадежны;

3) ремонт резервированной системы не производится.

С учетом (2.4) и (4.2) вероятность безотказной работы системы

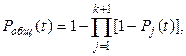(4.12)

где P_j(t) - вероятность безотказной работы j- цепи (устройства) в течение наработки (0, t);

(1-P_j(t)) - вероятность отказа j- цепи в течение наработки (0, t);

k+1—число соединен­ных параллельно на логической схеме цепей (устройств) .

При равнонадежных устройствах и показательном распределении наработки до отказа в случае общего ре­зервирования:

- вероятность безотказной работы

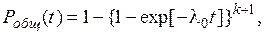(4.13)

где λ₀ - интенсивность отказов одного устройства определяется согласно (4.7);

- средняя наработка до отказа

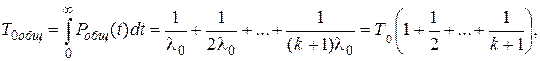(4.14)

где Т₀ = 1/λ₀ – средняя наработка до отказа одного устройства;

- интенсивность отказов

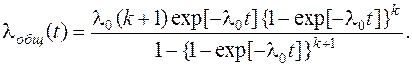(4.15)

В тех случаях, когда 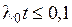, имеем:

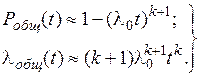(4.16)

Раздельное резервирование

Логическая схема устройства представлена на рис. 4.2,б.

При раздельном резервировании вероятность безотказной работы системы

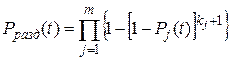, (4.17)

где P_j(t) – вероятность безотказной работы j–го элемента (участка резервирования) в течении наработки (0, t); m – число участков резервирования; (k_j+1) – число параллельно соединенных на логической схеме элементов в j–м участке резервирования.

При равнонадежных элементах и показательном распределении наработки до отказа

- вероятность безотказной работы

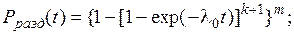(4.18)

- средняя наработка до отказа

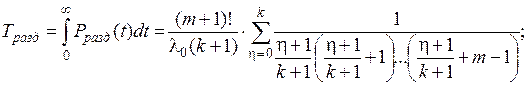(4.19)

- интенсивность отказов

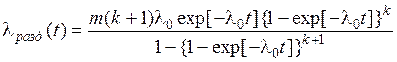. (4.20)

В случае, когда 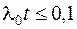, имеем:

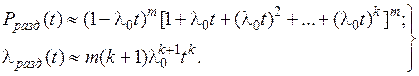(4.21)

4.4.1.3. Общее резервирование с дробной кратностью

При общем резервировании с дробной кратностью для определения вероятности безотказной работы системы используется биномиальный закон распределения.

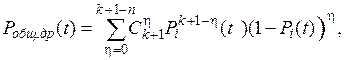(4.22)

где η – количество отказавших устройств, при которых резервированная система остается работоспособной ( η = 0,1,…, (к+1-n),

n- необходимое число работоспособных устройств из общего числа (к+1) устройств,

P_i(t) – вероятность безотказной работы основного или любого резервного устройства в течение наработки (0, t).

При показательном распределении наработки до отказа:

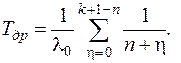(4.23)

При резервировании элементов с двумя видами от­казов (обрыв и короткое замыкание) рассматривают не логические, а электрические схемы соединений элемен­тов.

Вероятность обрыва и короткого замыкания обозна­чим соответственно q₀(t) и q_S(t).

Для расчета Q(t) - вероятности от­каза схемы с учетом двух видов отказов элементов составляется таблица всех возможных вариантов состоя­ний элементов схемы, выделяются комбинации, при ко­торых схема не работает, вычисляются и суммируются вероятности появления этих комбинаций.

Для схем (например, релейно-контактных), опреде­ленный вид отказа которых может быть вызван лишь од­ноименным видом отказа элемента, вероятность отказа определяется по формуле

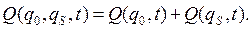
При последовательном электрическомсоединения m элементов

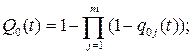(4.24)

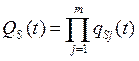. (4.25)

При параллельном электрическом соединении k +1элементов

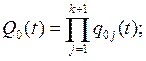(4.26)

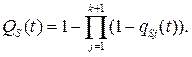(4.27)

4.4.2. Резервирова­ние замещением ненагруженное и облегченное с абсолютно надёжными переключателями