Кванторы. Равносильные предикаты
1.Среди предикатов “x ³ 0” , “|x – 0,5| = 0,5”, “ 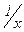 > 1”, “x ³ 1”, “x2 ³ 0”, “
> 1”, “x ³ 1”, “x2 ³ 0”, “ 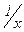 £ 1”, “x Î N”, “0< x < 1”, “x Î (0; 1)”, “x2 = 1”, “x Î Z Ù x > 0” найдите равносильные.
£ 1”, “x Î N”, “0< x < 1”, “x Î (0; 1)”, “x2 = 1”, “x Î Z Ù x > 0” найдите равносильные.
2.На каких из множеств N, Zили R равносильны предикаты а) “x ³ 1” и “x2 ³ 0”, б) “x ³ 1” и “ 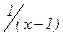 £ 1”, в) “x Î (–1; 0)” и “
£ 1”, в) “x Î (–1; 0)” и “ 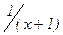 > 1”, г)“0 < x < 1” и “|x| < 1”, д) “0 < x < 1” и “|x – 0,5| = 0,5”.
> 1”, г)“0 < x < 1” и “|x| < 1”, д) “0 < x < 1” и “|x – 0,5| = 0,5”.
3.Для каждого из предикатов “х×(х – 1) > 0”, “ 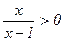 ”, “x > 0”, “0 £ x £ 1”, “x > 1”, “x < 0 Ú x > 1”, заданных на R, найдите все равносильные ему на множествах R, Z,N, N0 =N È {0}, R+ = {x Î R | x > 0}, R \ {0, 1}.
”, “x > 0”, “0 £ x £ 1”, “x > 1”, “x < 0 Ú x > 1”, заданных на R, найдите все равносильные ему на множествах R, Z,N, N0 =N È {0}, R+ = {x Î R | x > 0}, R \ {0, 1}.
4.Докажите, что если для предикатов P, Q , R, S на множестве A верно P º Q и R º S, то а) 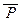 º
º 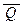 , б) P Ù R º Q Ù S, в) P Ú R º Q Ú S, г) P ® R º Q ® S,
, б) P Ù R º Q Ù S, в) P Ú R º Q Ú S, г) P ® R º Q ® S,
д) P « R º Q « S,е) " a Î A P(a) º " a Î A Q(a), ж) $ a Î A P(a) º $ a Î A Q(a).
5.Рассмотрим на множестве целых чисел предикаты P(x) = “x > 5”, Q(x) = “x – чётное целое число”, R(x) = “x < 9”, S(x, y) = “x > 2×y”, T(x, y) = “x M y”. “Переведите” на русский язык и определите истинностные значения высказываний:
а) P(5), б) S(13, 5), в) S(5, 2) Ù T(3, 1); г) " x Î Z (R(x) Ú P(x));
д) $ x Î Z S(x, 5) Ù Q(x); е) 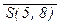 ; ж) " x Î Z (Q(x) Ù R(x) ® S(x, 1));
; ж) " x Î Z (Q(x) Ù R(x) ® S(x, 1));
з) " x Î Z ( 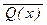 ® (" y Î Z (S(x, y) ®
® (" y Î Z (S(x, y) ® 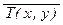 ))); и) $ y Î Z
))); и) $ y Î Z 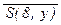 ;
;
к) $ x Î Z ( 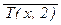 ®
® 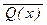 ) ; л) " z Î Z (P(z) Ú R(z)); м) R(0) ® S(3, 1).
) ; л) " z Î Z (P(z) Ú R(z)); м) R(0) ® S(3, 1).
6.Какие из высказываний с кванторами истинны, а какие ложны и почему ?
а) $ x Î R |x + 1| ³ 1, б) " y Î N (y > 3 ® y ³ 2), в) $ x Î R (x2 > 0 ® x < 0),
г) " z Î C (z – 2)×(z + 3) = (z – 4)×(z + 5),д) $ a ((a Î {3, 5}) ® (a2 – 6×a + 8 < 0)),
е) $ х Î R ((x2 – 5×x + 6 ³ 0) Ù (2×x2 – 4×x + 2 > 0)), ж) " b Î Z 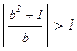 ,
,
з) " x Î Z |x + |x|| ³ |x|, и) $ z Î R |x + |x|| < |x|, к) " t Î R t2 – 5×t + 9 > 0,
л) $ с Î С с3 – 2×с + 1 = 0, м) " m Î {–1, 0, 2} m2 – m – 2 = 0, н) " x Î Z x M x,
о) " x Î R ($ y Î Z x > y), п) " x Î R ($ y Î Z x2 < y2), р) $ x Î R (" y Î Z x > y), с) $ а Î N ($b Î N a + b = a×b), т) $ x Î R ((" y Î Z |x + y| ³ 1) ® x = 0),
у) " x Î R (x > 1 ® ($ y Î Z |x + y| > 1)), ф) " а Î N ($b Î N a + b = a×b), х) " x Î R ($ y Î Z |x + y| > 1), ц) (" x Î R (x > 1)) ® ($ y Î Z |x + y| > 1)).
7.Докажите теорему об основных равносильностях с кванторами (см. приложение 4).
8.Приведите примеры, показывающие, что в общем случае
а) $ x Î A (" y Î A P(x, y)) 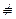 " y Î A ($ x Î A P(x, y));
" y Î A ($ x Î A P(x, y));
б) (" x Î A P(x, y)) Ú (" x Î A Q(x, y)) 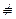 " x Î A (P(x, y) Ú Q(x, y));
" x Î A (P(x, y) Ú Q(x, y));
в) ($ x Î A P(x, y)) Ù ($ x Î A Q(x, y)) 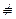 $ x Î A (P(x, y) Ù Q(x, y));
$ x Î A (P(x, y) Ù Q(x, y));
г) если R зависит от x, то
(" x Î А Р(х, y)) Ú R 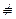 " x Î A (P(x, y) Ú R),
" x Î A (P(x, y) Ú R),
($ x Î А Р(х, y)) Ú R 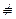 $ x Î A (P(x, y) Ú R),
$ x Î A (P(x, y) Ú R),
(" x Î А Р(х, y)) Ù R 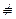 " x Î А (Р(x, y) Ù R),
" x Î А (Р(x, y) Ù R),
($ x Î А Р(х, y)) Ù R 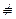 $ x Î А (Р(x, y) Ù R),
$ x Î А (Р(x, y) Ù R),
" х Î А (R ® Р(х, y)) 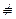 R ® (" x Î А Р(х, y)),
R ® (" x Î А Р(х, y)),
$ х Î А (R ® Р(х, y)) 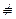 R ® ($ x Î А Р(х, y)).
R ® ($ x Î А Р(х, y)).
9.Верно ли, что для предиката R(y), не зависящего от x, верны равносильности:
а) (" x Î A P(x, y)) ® R(y) º " x Î A (P(x, y) ® R(y));
б) ($ x Î A P(x, y)) ® R(y) º $ x Î A (P(x, y) ® R(y));
б) (" x Î A P(x, y)) « R(y) º " x Î A (P(x, y) « R(y));
в) ($ x Î A P(x, y)) « R(y) º $ x Î A (P(x, y) « R(y)).
10.Докажите, что следующие высказывания истинны для любого одноэлементного множества A = {a} и любых предикатов на А:
а) $ y Î A (P(y) ® (" x Î А P(x))), б) $ x, y Î A ((P(x) Ú P(y)) ® P(x)), в) $ x Î A P(x), г) $ x, y Î A P(x, y), д) " x, y Î A (P(x) « P(y)), е) $ x Î A (P(x) ® P(y)).
11.Какие из высказываний задачи 9 будут истинны при A = {a, b} ? А при любом множестве A ?
12.Запишите в виде выражения с кванторами и предикатами высказывание, истинное только на одноэлементном множестве. А на двухэлементном ? А на трёхэлементном ? Можете ли Вы написать высказывание, истинное только для n-элементного множества ?
13.Запишите в виде выражений с кванторами и предикатами следующие утверждения и определите их истинностные значения:
а)для любого действительного числа x найдётся 0 < y < x;
б) если для действительного числа x найдётся 0 < y < x, то x > 0;
в) если для любого действительного числа x верно x ³ 0, то для любого y верно y £ 0 или y ³ x;
г) для любого действительного числа x,если x ³ 0, то для любого y верно y £ 0 или y ³ x;
д)если для любого y Î R верно y £ 0 или y ³ x, то x ³ 0;
е) если угол C треугольника АВС острый, то АС2 + ВС2 ¹ АС2 .
14.Используя равносильности с кванторами, сформулируйте отрицания утверждений. Определите истинностные значения исходного утверждения и полученного отрицания.
а) число a делится на 25, если оно оканчивается на 00, 50 или 75;
б)если сумма цифр числа делится на 5, то само число делится на 5;
в)в любом прямоугольнике диагонали равны;
г) если в четырёхугольнике диагонали равны, то он параллелограмм;
д) произведение любых двухдействительных чисел не превосходит суммы их квадратов;
е) произведение любых двухкомплексных чисел не превосходит суммы их квадратов;
ж) если внутренние накрест лежащие углы при пересечении двух прямых плоскости третьей прямой равны или сумма внутренних односторонних углов равна 180º, то прямые параллельны;
з) прямые в пространстве перпендикулярны, если они перпендикулярны некоторой третьей прямой.
